Combination circuits in series and parallel - Class 11
Summary
TLDREn este video, se explica cómo resolver un circuito combinado que involucra resistores en paralelo y en serie. El proceso incluye la determinación de una resistencia equivalente, el uso de la ley de Ohm para calcular la corriente y los voltajes en diferentes puntos del circuito, y la verificación de los resultados. El video cubre detalladamente cómo se resuelve paso a paso, desde la transformación de resistores en paralelo hasta el cálculo de corrientes y caídas de voltaje, ofreciendo una comprensión clara de los conceptos de circuitos eléctricos. Ideal para estudiantes de física.
Takeaways
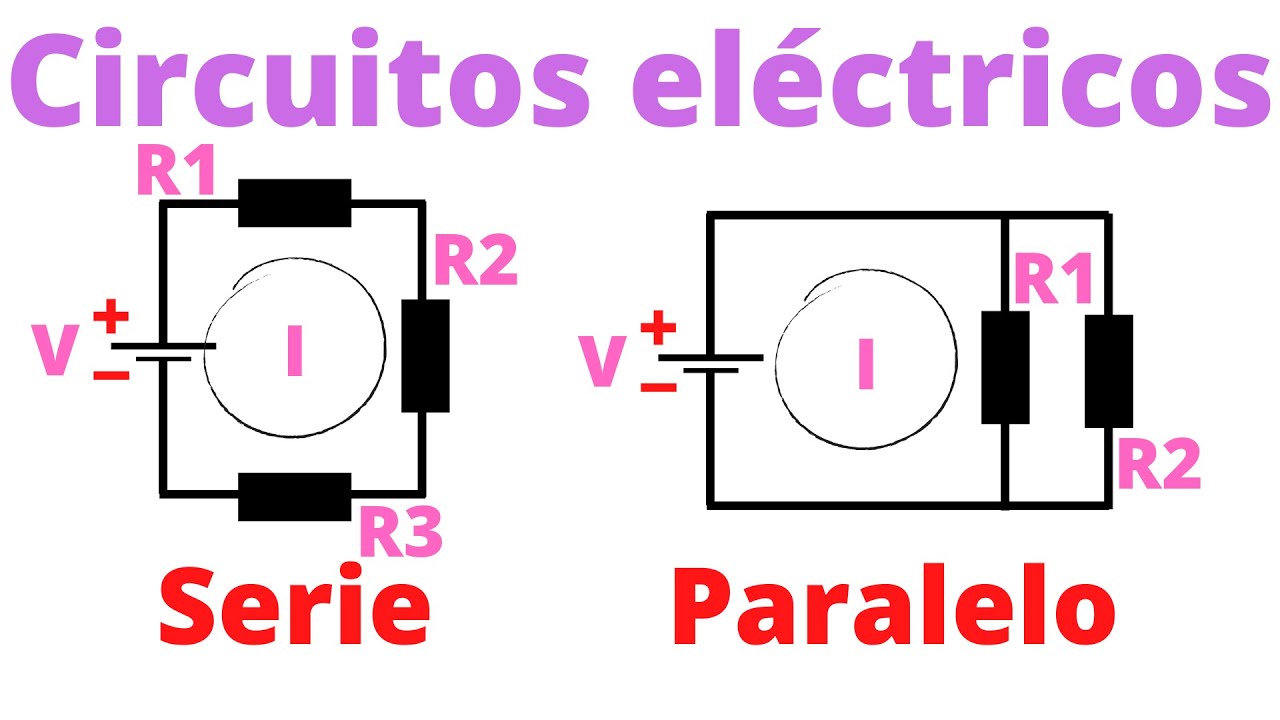
- 😀 El circuito de combinación consiste en dos resistores en paralelo conectados en serie con otros dos resistores.
- 😀 Se debe tratar este tipo de circuito como una combinación de resistores en paralelo y serie para analizarlo correctamente.
- 😀 El primer paso es encontrar la resistencia equivalente de los resistores en paralelo, usando la fórmula 1/R = 1/R1 + 1/R2.
- 😀 Para los dos resistores de 15 Ω en paralelo, la resistencia equivalente R1 es 10 Ω.
- 😀 La resistencia total del circuito en serie, R2, se calcula sumando las resistencias individuales: R2 = 20 Ω + 10 Ω + 15 Ω = 45 Ω.
- 😀 Usando la Ley de Ohm (V = I × R), se determina que la corriente total que pasa por el circuito es 2 A.
- 😀 Se calcula el voltaje en cada resistor del circuito utilizando la corriente y la resistencia de cada uno: 40 V en el resistor de 20 Ω, 20 V en el de 10 Ω y 30 V en el de 15 Ω.
- 😀 El voltaje total en el circuito debe ser igual a la fuente de 90 V, lo que confirma que las sumas de voltajes son correctas: 40 V + 20 V + 30 V = 90 V.
- 😀 La corriente a través del resistor de 30 Ω es 2/3 A, calculada usando la Ley de Ohm con la diferencia de voltaje de 20 V y la resistencia de 30 Ω.
- 😀 La corriente a través del resistor de 15 Ω es 4/3 A, calculada con la misma fórmula usando 20 V y 15 Ω.
- 😀 Al sumar las corrientes de los resistores de 30 Ω y 15 Ω, obtenemos la corriente total de 2 A, verificando que todo el análisis es correcto.
Q & A
¿Qué es un circuito combinado?
-Un circuito combinado es aquel en el que se encuentran resistores tanto en paralelo como en serie, como en este caso, donde dos resistores están en paralelo y estos se conectan en serie con otros dos resistores.
¿Cómo se calcula la resistencia equivalente de dos resistores en paralelo?
-La resistencia equivalente de dos resistores en paralelo se calcula usando la fórmula 1/R = 1/R1 + 1/R2. Luego, se resuelve para encontrar el valor de R.
¿Cómo se combinan las resistencias cuando están en serie?
-Cuando los resistores están en serie, se suman sus valores directamente. Es decir, la resistencia total en serie es igual a la suma de las resistencias individuales.
¿Cuál es la resistencia equivalente de los resistores de 30Ω y 15Ω en paralelo?
-La resistencia equivalente de los resistores de 30Ω y 15Ω en paralelo es 10Ω, calculada mediante la fórmula para resistores en paralelo.
¿Qué sucede cuando se combinan las resistencias equivalentes de 10Ω, 20Ω y 15Ω?
-Cuando se combinan las resistencias equivalentes de 10Ω, 20Ω y 15Ω en serie, se obtiene una resistencia total de 45Ω.
¿Cómo se calcula la corriente total en el circuito?
-La corriente total se calcula usando la ley de Ohm, dividiendo el voltaje total (90V) por la resistencia total del circuito (45Ω). Esto da una corriente total de 2A.
¿Cómo se determina la caída de voltaje en un resistor de 20Ω?
-La caída de voltaje en un resistor de 20Ω se calcula usando la ley de Ohm, multiplicando la corriente (2A) por la resistencia (20Ω), lo que da una caída de 40V.
¿Cómo se calculan las caídas de voltaje en los resistores de 10Ω y 15Ω?
-La caída de voltaje en el resistor de 10Ω es 20V (2A × 10Ω) y en el resistor de 15Ω es 30V (2A × 15Ω).
¿Por qué la corriente a través de los resistores en paralelo es diferente?
-La corriente a través de los resistores en paralelo es diferente debido a las resistencias distintas en cada rama. La corriente se distribuye inversamente proporcional a la resistencia de cada rama.
¿Cómo se verifica que la corriente total es la misma en todo el circuito?
-La corriente total se verifica sumando las corrientes en las ramas paralelas. La corriente que pasa por el resistor de 30Ω es 2/3A y por el resistor de 15Ω es 4/3A. La suma de estas corrientes es 2A, que es la corriente total del circuito.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)