Kirchhoff's Voltage Law (KVL)
Summary
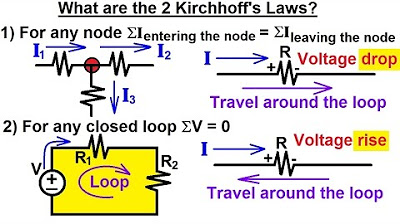
TLDRIn this lecture, the speaker explains Kirchhoff's Voltage Law (KVL), stating that the algebraic sum of voltages in a closed loop is zero. Using an example circuit with a voltage source and two resistors, the speaker walks through applying KVL to find the voltage drops across each component. They also introduce two different sign conventions for writing KVL equations, discussing the relationship between voltage, current, and resistance. Lastly, the speaker emphasizes the importance of understanding the concept behind KVL, based on energy conservation, to solve circuits effectively.
Takeaways
- 📏 The lecture begins with a discussion of KVL (Kirchhoff’s Voltage Law), stating that the algebraic sum of all voltages in a closed loop is zero.
- 🔋 In a closed loop with a voltage source (V), a resistor (R1), and another resistor (R2), the sum of voltage drops equals the total voltage supplied.
- 💡 KVL can be applied by adding up the voltage drops across each element in the loop, where voltage drops across resistors are calculated using Ohm’s law (V = IR).
- 🔄 The potential drop across a resistor is determined by multiplying the current (I) by the resistance (R).
- 🔍 Two conventions for writing KVL equations: the first considers a rise in potential as positive, while the second considers a rise as negative.
- 📝 Both conventions lead to the same result, with V = I * (R1 + R2), showing that the total voltage drop equals the source voltage.
- 🌍 KVL is based on the law of conservation of energy, as opposed to KCL (Kirchhoff's Current Law), which is based on the conservation of charge.
- ⚡ Voltage represents potential energy difference, meaning the energy to move a unit charge between two points is independent of the path taken.
- 🎯 KVL equations should include only potential differences (voltages) between points, not individual point potentials.
- 🔁 The lecture emphasizes that regardless of the chosen path in a circuit, following proper rules will always yield consistent results.
Q & A
What is KVL?
-KVL stands for Kirchhoff's Voltage Law, which states that the algebraic sum of all the voltages in any closed loop of a network is zero.
How do you apply KVL?
-To apply KVL, you calculate the sum of all voltages in a closed loop, considering their signs, and set this sum equal to zero.
What is the significance of the voltage source in the KVL equation?
-The voltage source in the KVL equation is represented by 'V' and is considered as a rise in potential, which is typically given a positive sign in the KVL equation.
What is the role of resistors in the KVL equation?
-Resistors in the KVL equation represent voltage drops across them, calculated as the product of current (I) and resistance (R), and are typically given a negative sign due to the drop in potential.
How does the direction of current flow affect the KVL equation?
-The direction of current flow determines whether the potential rises or drops. A rise in potential is associated with a positive sign, while a drop is associated with a negative sign in the KVL equation.
What are the conventions for writing KVL equations?
-There are two main conventions: one where a rise in potential is positive and a drop is negative, and another where the signs are reversed. The choice of convention depends on the direction chosen to traverse the loop.
Why is KVL based on the law of conservation of energy?
-KVL is based on the law of conservation of energy because voltage represents the potential energy difference across an element, and the energy required to move a unit charge between two points is independent of the path taken.
How do you calculate the potential difference between two points using KVL?
-To calculate the potential difference between two points using KVL, you choose a path between those points, apply KVL up to the second point, and equate the result to the potential at the second point.
Why can't you include the potential at a point directly in the KVL equation?
-You can't include the potential at a point directly in the KVL equation because KVL deals with potential differences (voltages), not absolute potentials.
What happens if you apply KVL starting from different points in the circuit?
-Applying KVL from different starting points should yield the same result for the potential difference between any two points, as long as the rules are followed correctly.
How does the choice of path affect the KVL equation?
-The choice of path affects the order in which voltages are added to the KVL equation, but the final result for the potential difference between any two points should be the same regardless of the path chosen.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
Electrical Engineering: Basic Laws (8 of 31) What Are Kirchhoff's Laws?

Kirchhoff's Voltage Law (KVL) - How to Solve Complicated Circuits | Basic Circuits | Electronics

KVL and KCL (Circuits for Beginners #11)

Kirchhoff's Voltage Law (KVL) Explained

Kirchhoff's voltage law | Circuit analysis | Electrical engineering | Khan Academy

Kirchhoff's Voltage Law - KVL Circuits, Loop Rule & Ohm's Law - Series Circuits, Physics
5.0 / 5 (0 votes)