Kirchhoff's voltage law | Circuit analysis | Electrical engineering | Khan Academy

Summary

This video script explains Kirchhoff's Voltage Law (KVL) in the context of circuit analysis. It uses a simple circuit with a voltage source and resistors to demonstrate the concept of voltage rises and drops. The script clarifies that the sum of voltage rises minus the sum of voltage drops equals zero, which is KVL. It illustrates this with a single resistor and then generalizes it for circuits with multiple resistors, emphasizing that KVL applies regardless of the starting point or direction in the circuit loop.

Takeaways

• 🔌 Kirchhoff's Voltage Law (KVL) is a fundamental principle in circuit analysis.
• 📈 The law states that the algebraic sum of the voltage rises and drops in any closed loop of a circuit is zero.
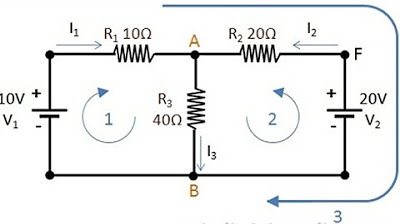
• 🔢 A voltage source of 10 volts and a resistor of 200 ohms are used as an example in the script.
• 📉 The concept of voltage rise (going through a voltage source) and voltage drop (across a resistor) is explained.
• 🔄 The voltage drop is equal and opposite to the voltage rise, meaning they cancel each other out.
• 🔄 The voltage at any point in the circuit can be determined by the sum of the voltage rises and drops from a reference point.
• 🔗 KVL can be applied to any loop in a circuit, regardless of the starting point.
• 🔄 The law applies to circuits with multiple resistors, as demonstrated with two 100-ohm resistors.
• 🔢 The script provides a mathematical representation of KVL: v-rise - v-drop = 0.
• 🔧 KVL is a tool for circuit analysis, often used alongside Kirchhoff's Current Law (KCL).

Q & A

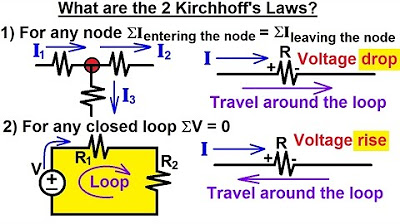
What is Kirchhoff's Voltage Law (KVL)?

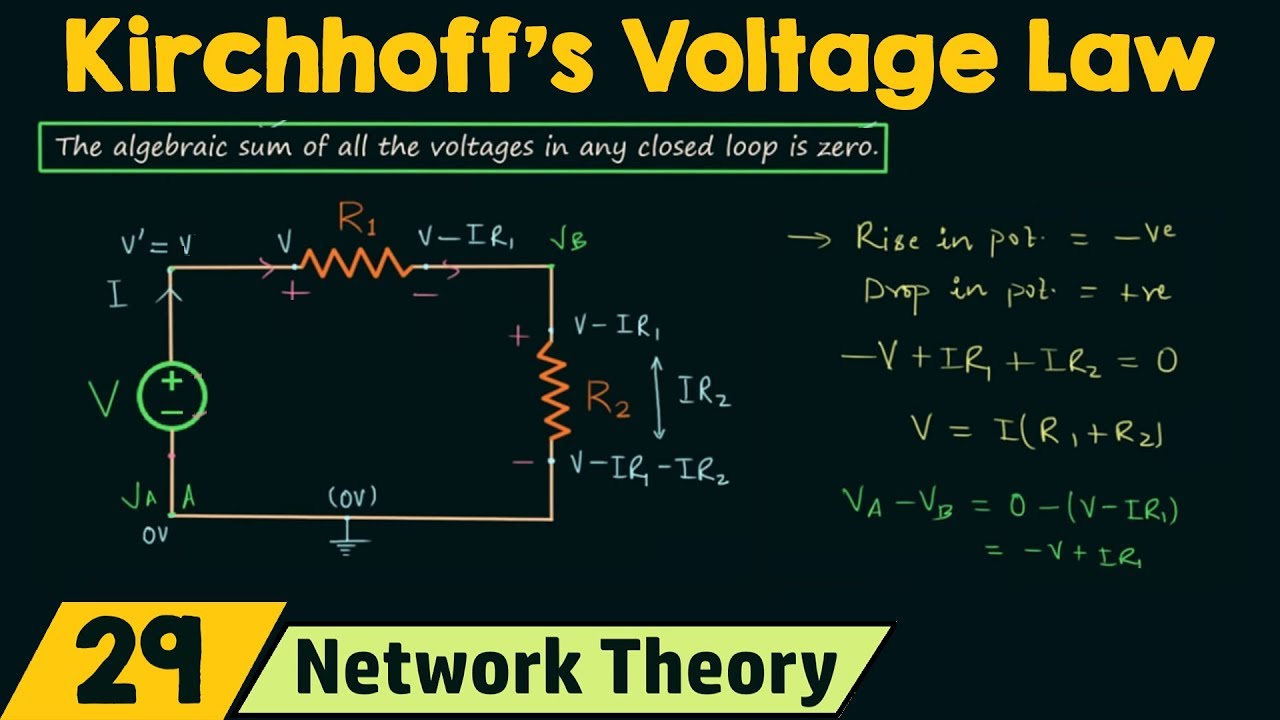
Kirchhoff's Voltage Law states that the sum of the voltage rises and the sum of the voltage drops around a closed loop in a circuit is always equal to zero.

How is voltage rise and voltage drop defined in the script?

A voltage rise occurs when the voltage increases as you move through a component (e.g., a voltage source), while a voltage drop occurs when the voltage decreases, such as when passing through a resistor.

What happens to the total voltage when you go around a complete loop in a circuit?

The total voltage rise minus the total voltage drop around a complete loop equals zero, meaning you return to the same voltage level you started with.

In the example circuit with one 200-ohm resistor and a 10-volt source, what are the voltage rises and drops?

There is a voltage rise of 10 volts across the voltage source and a voltage drop of 10 volts across the 200-ohm resistor.

What does the script mean by 'v-rise minus v-drop equals zero'?

It means that the total voltage gained from voltage rises equals the total voltage lost from voltage drops, which is the essence of Kirchhoff's Voltage Law.

How does the circuit behave when two 100-ohm resistors are added to the 10-volt source?

The circuit has a 10-volt rise at the source and two voltage drops of 5 volts each across the two resistors, summing to zero when completing the loop.

How do you label node voltages in a circuit?

Node voltages are labeled relative to a reference point, often chosen as zero volts (ground). For example, the node connected to the positive terminal of a 10-volt source is labeled as 10 volts.

Can Kirchhoff's Voltage Law be applied if we start at any point in the circuit?

Yes, KVL applies no matter where you start in the loop, and no matter the direction in which you traverse the loop.

What happens if you go counterclockwise instead of clockwise around the circuit?

The voltage rises and drops will still sum to zero, regardless of the direction you go around the loop.

What tools are mentioned for circuit analysis alongside Kirchhoff's Voltage Law?

Kirchhoff's Voltage Law is paired with Kirchhoff's Current Law (KCL) to form essential tools for analyzing circuits.

Outlines

00:00

🔌 Introduction to Kirchhoff's Voltage Law

This paragraph introduces Kirchhoff's Voltage Law (KVL) as a fundamental principle for analyzing circuits. It begins by explaining the concept of voltage rise and drop using a simple circuit with a 10-volt source and a 200-ohm resistor. The narrator labels nodes in the circuit and demonstrates how the voltage changes as it passes through the resistor, either rising or dropping by 10 volts. The key takeaway is that the sum of all voltage rises and drops in any part of a circuit equals zero, which is the essence of KVL. The paragraph concludes with a practical example of applying KVL to a circuit with two resistors, showing that the sum of voltage rises minus the sum of voltage drops equals zero.

05:02

🔄 Applying Kirchhoff's Voltage Law to Circuit Loops

This paragraph delves deeper into the application of Kirchhoff's Voltage Law (KVL) by considering a circuit with two resistors of 100 ohms each. It explains how to calculate the voltage at different nodes within the circuit and emphasizes that KVL can be applied starting from any node and moving in any direction around the circuit. The narrator illustrates this by showing that whether you move clockwise or counterclockwise around the circuit, the sum of voltage rises minus the sum of voltage drops will always equal zero. The paragraph concludes by highlighting that KVL, when paired with Kirchhoff's Current Law, forms the basis for analyzing and understanding complex circuits.

Keywords

💡Kirchhoff's Laws

Kirchhoff's Laws are fundamental principles used in circuit analysis. They consist of Kirchhoff's Current Law (KCL) and Kirchhoff's Voltage Law (KVL). In the context of the video, Kirchhoff's Voltage Law is the focus, which states that the algebraic sum of the voltage rises and drops in any closed loop of a network is zero. This law is crucial for analyzing circuits as it helps determine the voltage across various components within the circuit.

💡Kirchhoff's Voltage Law (KVL)

Kirchhoff's Voltage Law (KVL) is one of the two Kirchhoff's laws, which is central to the video's theme. KVL asserts that the sum of all the voltage rises and drops in any closed loop of a circuit is zero. This law is used to set up equations that can be solved to find the voltages and currents in a circuit. The video script uses KVL to demonstrate how to calculate the voltage across resistors in a simple circuit.

💡Voltage Source

A voltage source is a device that provides a specified electromotive force (EMF) to a circuit. In the video, a 10-volt voltage source is used as an example to illustrate how voltage rises when moving through the source. It is a key component in the circuit diagrams used to explain KVL.

💡Resistor

A resistor is a passive component in a circuit that opposes the flow of electric current, causing a voltage drop across it. The video mentions a 200-ohm resistor and later two 100-ohm resistors to demonstrate how voltage drops across them according to Ohm's Law (V=IR).

💡Voltage Rise

Voltage rise refers to an increase in voltage as one moves through a voltage source in a circuit. The video script uses the term to describe the increase from zero volts to ten volts when moving through a 10-volt source, which is a fundamental concept in understanding KVL.

💡Voltage Drop

Voltage drop is the decrease in voltage across a component, such as a resistor, due to its resistance. In the video, the script describes a voltage drop from 10 volts to zero volts across a resistor, which is essential for applying KVL to analyze circuits.

💡Ohm's Law

Ohm's Law relates the voltage (V), current (I), and resistance (R) in an electrical circuit (V=IR). Although not explicitly mentioned in the script, Ohm's Law is implicitly used to explain voltage drops across resistors, which is a prerequisite for understanding KVL.

💡Node

In the context of the video, a node refers to a point in a circuit where two or more components are connected. The script labels nodes with voltage values to demonstrate how voltage changes as one moves through different parts of the circuit, which is vital for applying KVL.

💡Circuit Analysis

Circuit analysis is the process of determining the behavior of a circuit using mathematical tools and physical laws. The video focuses on using Kirchhoff's Voltage Law for circuit analysis, which is essential for predicting how electrical circuits will behave under various conditions.

💡Summation

The term 'summation' in the video refers to the process of adding up all the voltage rises and drops in a circuit loop to apply KVL. The script uses summation to show that the total voltage change around any closed loop in a circuit is zero, which is a key step in solving for unknowns in circuit analysis.

💡Loop

A loop in the context of the video is any closed path within a circuit. The script explains that KVL can be applied to any loop in a circuit, regardless of the starting point, to ensure that the sum of voltage rises and drops equals zero, which is a fundamental principle of KVL.

Highlights

Introduction to Kirchhoff's laws as essential tools for circuit analysis.

Explanation of Kirchhoff's voltage law (KVL) in the context of circuit analysis.

Example of a simple circuit with a 10-volt source and a 200-ohm resistor.

Labeling of nodes and understanding voltage rises and drops in a circuit.

Definition of voltage rise and drop in the context of a circuit.

Observation that voltage rises and drops in a circuit sum to zero.

Equation v-rise - v-drop = 0 as a representation of KVL.

Application of KVL to a circuit with two resistors.

Explanation of how voltage drops are calculated across equal resistors.

Generalization of KVL to include the summation of voltage rises and falls.

Introduction of the summation symbol for representing voltage changes.

Compact form of KVL using a single summation symbol around a loop.

Explanation that starting at any corner of the circuit and going around the loop results in zero sum.

Emphasis on the flexibility of starting at any node and going in any direction for KVL.

Introduction of Kirchhoff's voltage law (KVL) as a fundamental principle in circuit analysis.

Highlight that KVL works regardless of the starting node or direction chosen.

Mention of pairing KVL with Kirchhoff's current law for comprehensive circuit analysis.

Transcripts

- [Voiceover] Now we're ready to start hooking up

our components into circuits, and one of the two things

that are going to be very useful to us are Kirchhoff's laws.

In this video we're gonna talk

about Kirchhoff's voltage law.

If we look at this circuit here,

this is a voltage source, let's just say this is 10 volts.

We'll put a resistor connected to it

and let's say the resistor is 200 ohms.

Just for something to talk about.

One of the things I can do here is I can label this

with voltages on the different nodes.

Here's one node down here.

I'm going to arbitrarily call this zero volts.

Then if I go through this voltage source,

this node up here is going to be at 10 volts.

10 volts.

So here's a little bit of jargon.

We call this voltage here.

The voltage goes up as we go through the voltage source,

and that's called a voltage rise.

Over on this side, if we are standing

at this point in the circuit right here

and we went from this node down to this node,

like that, the voltage would go from 10 volts

down to zero volts in this circuit,

and that's called a voltage drop.

That's just a little bit of slang, or jargon

that we use to talk about changes in voltage.

Now I can make an observation about this.

If I look at this voltage rise here, it's 10 volts,

and if I look at that voltage drop, the drop is 10 volts.

I can say the drop is 10 volts,

or I could say the rise on this side is minus 10 volts.

A rise of minus 10.

These two expressions mean exactly the same thing.

It meant that the voltage went from 10 volts

to zero volts, sort of going through this 200 ohm resistor.

So I ran a little expression for this,

which is, v-rise minus v-drop equals what?

Equals zero.

I went up 10 volts, back down 10 volts,

I end up back at zero volts, and that's this right here.

This is a form of Kirchhoff's voltage law.

It says the voltage rises minus

the voltage drops is equal to zero.

So if we just plug our actual numbers in here

what we get is 10 minus 10 equals zero.

I'm gonna draw this circuit again.

Let's draw another version of this circuit.

This time we'll have two resistors instead of one.

We'll make it...

We'll make it two 100 ohm resistors.

Let's go through and label these.

This is again 10 volts.

So this node is at zero volts.

This node is at 10 volts.

What's this node?

This node here is...

These are equal resistors,

so this is gonna be at five volts.

That's this node voltage here with respect to here.

So that is five volts.

This is five volts.

And this is 10 volts.

So let's just do our visit again.

Let's start here and count the rises and drops.

We go up 10 volts, then we have a voltage drop of five,

then we have another voltage drop of five,

and then we get back to zero.

We can write the sum of the rises

and the falls just like we did before.

We can say 10 volts minus five minus five equals zero.

Alright.

So I can generalize this.

We can say this is general we can do the summation,

that's the summation symbol,

of the v-rise minus the sum of the v-fall equals zero.

This is a form of Kirchhoff's voltage law.

The sum of the voltage rises minus the sum

of the voltage falls is always equal to zero.

There's a more compact way to write this

that I like better, and that is, we start at this corner...

We start at any corner of the circuit.

Let's say we start here.

We're gonna go up 10 volts, down five volts,

and down five volts.

So what we're adding is the voltage rises.

We're adding all the voltage rises.

Rise plus 10.

That's a rise of minus five and a rise of minus five.

So I can write this with just one summation symbol.

The voltages around the loop, where i takes us all

the way around the loop, equals zero.

So this means I start any place on the circuit,

go around in some direction, this way or this way,

up, down, down, and I end up back

at the same voltage I started at.

So let's put a box around that too.

This is Kvl, Kirchhoff's voltage law.

Now I started over here in this corner,

but I could start anywhere.

If I started at the top and went

around clockwise, if I started here say,

I would go minus five, minus five, plus 10,

and I'd get the same answer.

I'd still get back to zero.

If I start here and I go around the other way,

the same thing happens.

Plus five rise, plus five rise,

and this is a 10 volt drop,

so it works whichever way you go around the loop,

and it works for whatever node you start at.

That's the essence of Kirchhoff's voltage law.

We're gonna pair this with the current law,

Kirchhoff's current law, and with those two,

that's our tools for doing circuit analysis.