Standard Error of the Mean: Concept and Formula | Statistics Tutorial #6 | MarinStatsLectures

Summary

The script explains the concept of standard error of the sample mean, which is the standard deviation of the sample mean (Σ/√n). It starts by discussing variance properties, such as how the variance of a constant times a variable is the constant squared times the variance of the variable. It then applies these properties to the sample mean, showing that the variance of the sample mean is the population variance divided by the sample size. The standard error is derived as the square root of this variance, resulting in the formula Sigma/√n, highlighting the switch from population to sample standard deviation when dealing with samples.

Takeaways

• 📐 The standard deviation of the sample mean is also known as the standard error of the sample mean.
• 🔢 It is calculated as the population standard deviation (sigma) divided by the square root of the sample size (n).
• 📚 Two key properties used in the explanation are: (1) variance of a times X equals a squared times the variance of X, and (2) variance of X1 plus X2 equals the sum of their individual variances if they are independent.
• 🧮 The variance of the sample mean is derived by considering the mean of X1 to Xn divided by n, assuming each observation has the same mean and variance.
• 📉 The variance of the sample mean is expressed as 1/n squared times the variance of X1 to Xn.
• 🔄 By taking the constant out of the variance, it simplifies to 1/n squared times the sum of individual variances of each observation.
• 🔄 Since each observation's variance is sigma squared, the formula becomes 1/n squared times n times sigma squared.
• 🔄 The n in the numerator and denominator cancels out, leaving the variance of the sample mean as sigma squared over n.
• 📏 The standard deviation of the sample mean, or standard error, is the square root of the variance of the sample mean, which simplifies to sigma over the square root of n.
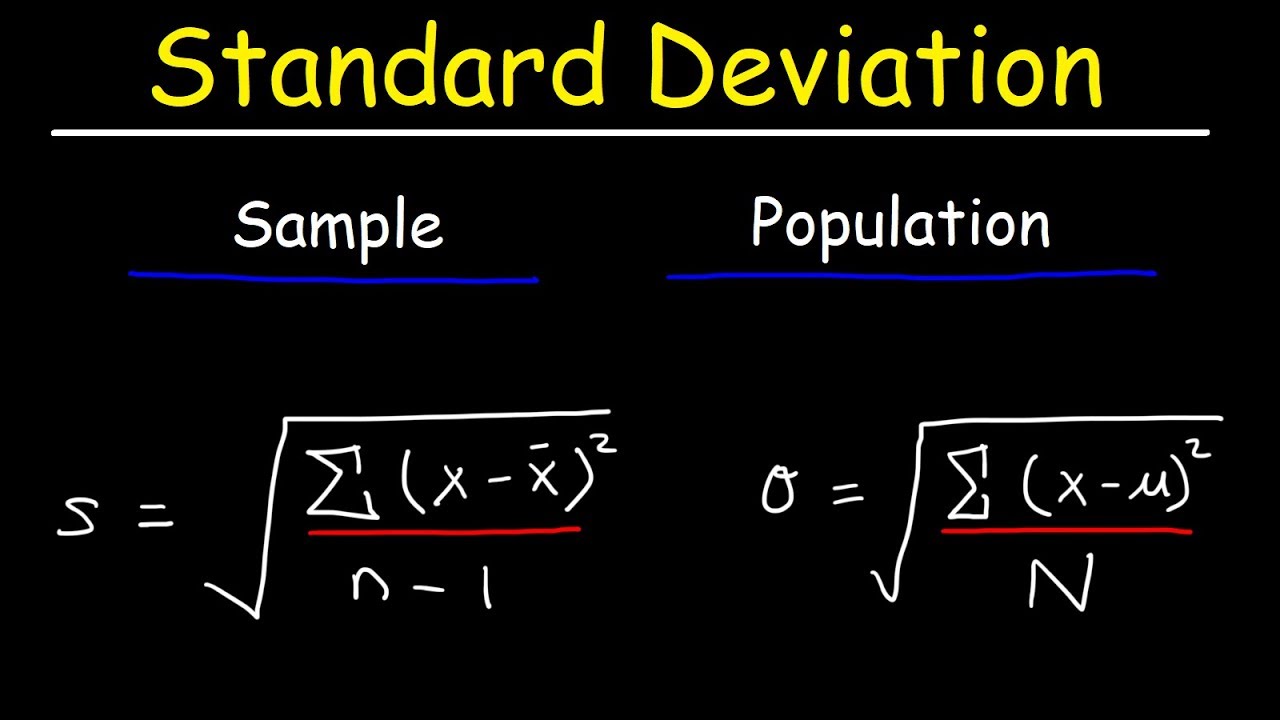
• 📋 When dealing with samples, the term 'standard error' replaces 'standard deviation' and the sample standard deviation is used instead of the population standard deviation.

Q & A

What is the standard deviation of the sample mean also known as?

The standard deviation of the sample mean is also known as the standard error of the sample mean.

Why is the standard deviation of the sample mean expressed as Sigma over the square root of n?

The standard deviation of the sample mean is expressed as Sigma over the square root of n because it represents the standard deviation of the sampling distribution of the sample mean, where Sigma is the population standard deviation and n is the sample size.

What is the first property mentioned in the script that is used to calculate the variance of a constant times a random variable?

The first property mentioned is that the variance of a times X (where a is any constant) is equal to a squared times the variance of X.

What is the second property used in the script to calculate the variance of the sum of independent random variables?

The second property is that the variance of x1 plus x2 (assuming x1 and x2 are independent) is the sum of their individual variances, which can be expressed as the variance of x1 plus the variance of x2.

What is the assumption made about the observations in the sample when calculating the variance of the sample mean?

The assumption made is that each observation in the sample (x1, x2, ..., xn) has the same mean and the same variance, implying that the sample is a random sample from a distribution.

How is the variance of the sample mean initially expressed in the script?

The variance of the sample mean is initially expressed as the variance of the sum of x1, x2, ..., xn divided by n, which is essentially the definition of the sample mean.

What does the script suggest about the independence of the observations in the sample?

The script suggests that the observations in the sample are independent of one another, which is a common assumption when dealing with random samples.

What is the formula for the variance of the sample mean derived from the properties discussed in the script?

The formula for the variance of the sample mean derived from the properties is 1 over N squared times the sum of the variances of x1 to xn, which simplifies to Sigma squared over N, where Sigma squared is the population variance.

What is the relationship between the standard deviation of the sample mean and the population standard deviation?

The standard deviation of the sample mean, also known as the standard error, is the population standard deviation (Sigma) divided by the square root of the sample size (n).

Why do we start calling the standard deviation of the sample mean the standard error when dealing with samples?

We start calling it the standard error when dealing with samples to differentiate it from the population standard deviation and to emphasize that it is an estimate of the variability of the sample mean around the population mean.

What does the script imply about the use of sample standard deviation in place of the population standard deviation?

The script implies that when the population standard deviation is unknown, the sample standard deviation is used in its place to estimate the standard error of the sample mean.