Position Vectors and Displacement Vectors - Physics

Summary

This video tutorial explains the concept of position vectors and their application in calculating displacement vectors. It starts with a 2D example, showing how to find the position vector from the origin to a point (3,2), represented as 3i + 2j. The tutorial then extends to 3D, illustrating how to determine the position vector for a point (3,4,5), expressed as 3i + 4j + 5k. It further discusses how to calculate the magnitude of a vector using the square root of the sum of squares of its components. Finally, it demonstrates how to find the displacement vector when a particle moves from point A (2,3,4) to point B (5,-2,8), by subtracting the initial position vector from the final one.

Takeaways

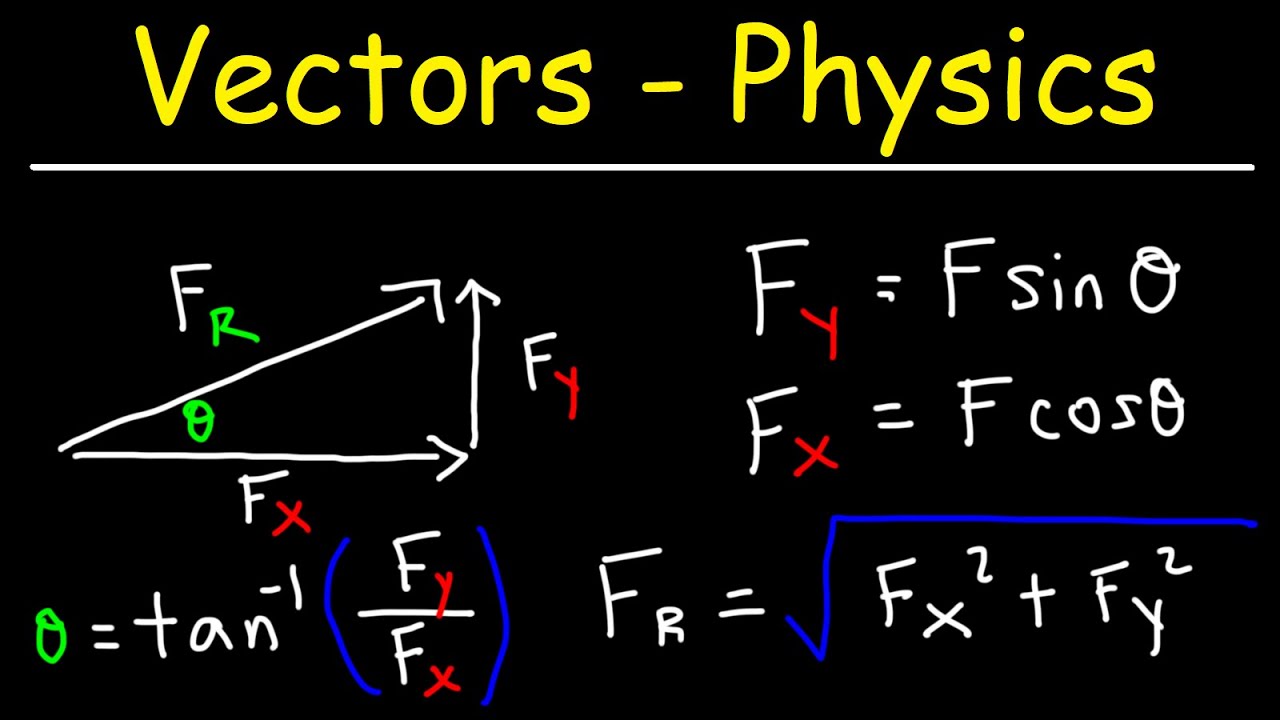
• 📝 Position vectors are vectors that start from the origin and point to a specific point in space.
• 📝 The position vector for a point P(3, 2) in a 2D coordinate system is represented as 3i + 2j, indicating the direction and distance from the origin to point P.
• 📝 In a 3D coordinate system, a position vector for a point P(3, 4, 5) is represented as 3i + 4j + 5k, showing the x, y, and z components of the vector.
• 📝 The magnitude or length of a position vector in a 2D system is calculated using the formula √(x^2 + y^2), while in 3D it's √(x^2 + y^2 + z^2).
• 📝 The magnitude of the position vector for point P(3, 4, 5) is √(3^2 + 4^2 + 5^2) = √(50) = 5√2.
• 📝 Displacement vector is calculated by subtracting the initial position vector from the final position vector, representing the change in position.
• 📝 For a particle moving from point A(2, 3, 4) to point B(5, -2, 8), the displacement vector is found by subtracting the position vector of A from B.
• 📝 The displacement vector from A to B is calculated as (5i - 2j + 8k) - (2i + 3j + 4k) = 3i - 5j + 4k.
• 📝 The video provides a resource for further learning with an ebook on passing math and science classes available at video.tutor.net.
• 📝 The first chapter of the ebook can be obtained for free by joining the email list mentioned in the video.

Q & A

What are position vectors?

Position vectors are vectors that start from the origin and point to a particular point in a coordinate system. They are represented by the symbol 'r' with a vector symbol attached to it.

How do you draw a position vector for a point in a 2D coordinate system?

To draw a position vector for a point in a 2D coordinate system, you draw it from the origin to the point of interest, using the x and y coordinates of the point.

What is the position vector for a point P with coordinates (3, 2) in a 2D coordinate system?

The position vector for point P with coordinates (3, 2) in a 2D coordinate system is 3i + 2j, where 3i represents the x-component and 2j represents the y-component.

How do you calculate the position vector in a 3D coordinate system?

In a 3D coordinate system, the position vector is calculated by traveling along the x, y, and z directions from the origin to the point of interest, using the x, y, and z coordinates of the point.

What is the formula to find the magnitude of a position vector in a 2D coordinate system?

The magnitude of a position vector in a 2D coordinate system is found using the formula: √(x² + y²), where x and y are the components of the vector.

How do you find the magnitude of a position vector in a 3D coordinate system?

The magnitude of a position vector in a 3D coordinate system is calculated using the formula: √(x² + y² + z²), where x, y, and z are the components of the vector.

What is the displacement vector and how is it different from a position vector?

The displacement vector represents the change in position of an object as it moves from one point to another. It is different from a position vector because it is the difference between two position vectors.

How do you calculate the displacement vector when a particle moves from point A to point B?

To calculate the displacement vector when a particle moves from point A to point B, you subtract the position vector of point A from the position vector of point B: R_B - R_A.

What is the position vector for point A with coordinates (2, 3, 4) in a 3D coordinate system?

The position vector for point A with coordinates (2, 3, 4) in a 3D coordinate system is 2i + 3j + 4k.

What is the position vector for point B with coordinates (5, -2, 8) in a 3D coordinate system?

The position vector for point B with coordinates (5, -2, 8) in a 3D coordinate system is 5i - 2j + 8k.

How do you find the displacement vector when a particle moves from point A to point B with given coordinates?

To find the displacement vector from point A to point B, calculate the difference between their position vectors: (5i - 2j + 8k) - (2i + 3j + 4k), which results in 3i - 5j + 4k.

Outlines

00:00

📐 Understanding Position Vectors

This paragraph introduces the concept of position vectors, which are vectors that start from the origin and point to a specific point of interest in a coordinate system. The video explains how to calculate a position vector by taking the differences in the x and y values from the origin to the point of interest. For a 2D coordinate system, the position vector for a point P at (3,2) is calculated as 3i + 2j. The video then extends this concept to a 3D coordinate system, showing how to find the position vector for a point P at (3,4,5), which is 3i + 4j + 5k. The paragraph concludes with a question about how to determine the length of a position vector, explaining that for a 2D system, it's the square root of the sum of the squares of the x and y components, and for a 3D system, it includes the square of the z component as well.

05:01

🔍 Calculating Displacement Vectors

The second paragraph focuses on how to calculate a displacement vector using position vectors. It provides an example of a particle moving from point A (2,3,4) to point B (5,-2,8) in a 3D space. The position vectors for points A and B are determined to be 2i + 3j + 4k and 5i - 2j + 8k, respectively. The displacement vector, which represents the change in position from A to B, is found by subtracting the initial position vector (point A) from the final position vector (point B). The resulting displacement vector is 3i - 5j + 4k. The paragraph also mentions a website, video.tutor.net, where viewers can find resources to improve their math and science skills.

Keywords

💡Position Vector

A position vector is a mathematical representation of a point's location in space, starting from the origin and extending to the point of interest. In the video, it is used to describe how to represent a point P (3,2) in a 2D coordinate system and a point (3,4,5) in a 3D coordinate system. The vector is denoted by a lowercase letter with a vector symbol (e.g., r) and is calculated by subtracting the origin's coordinates from the point's coordinates.

💡Origin

The origin is the starting point of a coordinate system, represented by the coordinates (0,0) in 2D or (0,0,0) in 3D. It serves as the reference point from which position vectors are drawn. The video explains that position vectors start at the origin and point towards a specific point of interest.

💡Displacement Vector

A displacement vector represents the change in position of an object. It is calculated by finding the difference between the final and initial position vectors. The video illustrates this by calculating the displacement vector as a particle moves from point A (2,3,4) to point B (5,-2,8) in a 3D space.

💡Magnitude

The magnitude of a vector is its length or size, calculated using the Pythagorean theorem for 2D vectors and extending to three dimensions for 3D vectors. The video explains how to find the magnitude of a 3D position vector by taking the square root of the sum of the squares of its components.

💡X-axis

The x-axis is one of the fundamental axes in a Cartesian coordinate system, representing horizontal direction. In the video, it is used to describe the horizontal component of a position vector.

💡Y-axis

The y-axis is another fundamental axis in a Cartesian coordinate system, representing vertical direction. The video uses the y-axis to describe the vertical component of a position vector.

💡Z-axis

In a 3D coordinate system, the z-axis represents the depth or height direction. The video introduces the z-axis when explaining how to calculate position vectors in three-dimensional space.

💡Component

A component of a vector refers to its individual parts along each axis. The video breaks down position vectors into their x, y, and z components, showing how these components are calculated by subtracting the origin's coordinates from the point's coordinates.

💡i, j, k

In the context of the video, i, j, and k are unit vectors representing the x, y, and z axes, respectively. They are used to express the components of a position vector in a compact form, such as 3i + 4j + 5k for a 3D vector.

💡Square Root

The square root operation is used in the video to calculate the magnitude of a vector. It is applied to the sum of the squares of the vector's components to find the length of the vector.

💡Coordinate System

A coordinate system is a framework that uses numbers to specify points in a plane or space. The video discusses both 2D and 3D coordinate systems, explaining how position vectors are used to represent points within these systems.

Highlights

Introduction to position vectors and their use in calculating displacement vectors.

Definition of position vectors as vectors starting from the origin to a point of interest.

Visual representation of a position vector from the origin to point P at (3,2) on a 2D graph.

Explanation of how to write a position vector in terms of its x and y components.

Example calculation of a 2D position vector as 3i + 2j.

Description of how to visualize moving from the origin to point P using the position vector.

Introduction to 3D coordinate systems and position vectors in 3D space.

Example of a 3D position vector for a point P at (3,4,5) as 3i + 4j + 5k.

Question posed to the viewer about determining the length of a position vector.

Explanation of finding the magnitude of a position vector for both 2D and 3D systems.

Calculation of the magnitude of a 3D position vector using the formula √(x² + y² + z²).

Example calculation of the magnitude of a 3D position vector as √(9 + 16 + 25).

Introduction to the concept of displacement vectors.

Description of how to find the position vectors for points A (2,3,4) and B (5,-2,8).

Instruction on calculating the displacement vector as the difference between the position vectors of points A and B.

Example calculation of the displacement vector from A to B as (3i - 5j + 4k).

Promotion of the speaker's website, video.tutor.net, for additional educational resources.

Invitation to join the speaker's email list for a free chapter of an ebook on passing math and science classes.

Transcripts

in this video we're going to talk about

position vectors and how to use them to

calculate a displacement vector

so what are position vectors

to answer that question let's draw a

picture

so here we have a graph that's the

x-axis this is the y-axis

and let's put a point on this graph

we'll call this point p

which is at 3 comma two

now to draw the position vector we're

going to draw it from the origin

to the point of Interest

so that's the position Vector it's a

vector that starts from the origin and

points to a particular point

it's represented by the symbol

r

with a vector symbol attached to it

now the origin is at 0 0.

to write a vector between two points

it's simply the difference

in the X values

and the difference in the Y values

so I'm subtracting 3 minus 0 to get the

X component of the vector

and then I'm subtracting the Y values 2

minus 0 to get the Y component of the

position vector

so the position Vector for this example

is 3i plus 2J

so this is the X component and this is

the Y component of the position vector

and you can see that visually

to go from the origin to point P we need

to travel three units along the X

Direction and two units along the Y

Direction

and so we can see why it's 3i plus 2J so

that's how you could find the position

Vector remember it starts at the origin

and it's directed towards the point of

Interest

let's try another example but with a 3D

coordinate system

so let's say this is the z-axis

we'll say this is the x-axis

and this is the y-axis

now let's say we have some point p

which is that

3 comma four comma 5. so this is X Y Z

so to get that to that point starting

from the origin

we need to travel three units

along the X Direction

and then four units

along the y direction and then up

five units along the Z Direction

so here is our position Vector r

so it's going to be 3i

plus 4J

plus 5K

now here's a question for you how can we

determine the length

of the position Vector r

how long is this position vector

in order to determine the less of the

position vector

you basically finding the magnitude

now

if it's for a 2d coordinate system it's

going to be the square root of x squared

plus y squared

but for a 3D coordinate system like the

example that we have is going to be also

plus a z squared inside of a square root

symbol

so for this problem it's going to be the

square root of 3 squared plus 4 squared

plus 5 squared

3 squared is 9 4 squared is 16. 5

squared is 25.

9 plus 16 is 25

plus 25 is 50.

so we have the square root of 50 which

we can reduce that

50 is 25 times 2 and the square root of

25 is 5.

so this is the magnitude of the position

Vector which is also the same as the

length of the position Vector so that's

how you could find the life of any

Vector really

now let's say we have a particle

that moves from point A

which is that

2 comma 3 comma 4.

and it's going to move to point B

and let's say that point B is located

at 5 negative 2 8.

so for this problem

find the position vectors that point to

point a and point B

and then use those position vectors to

calculate the displacement Vector as the

particle moves from point A to point B

now to find a position vector

for point a it's simply going to be

2i

plus 3j plus 4K

to find a position Vector for point B

it's simply

5i

minus two J plus a k

now to calculate the displacement vector

using

the position vectors it's going to be

the difference between the two

so as we go from A to B initial to final

it's going to be the final position

minus the initial position that gives us

displacement displacement is the change

in position

so we're going to take

R and B and subtract it by r a

and that's going to give us the

displacement vector

if we take the final position Vector

minus the initial position vector

we're going to get the displacement

vector

so I'm going to write it out so we have

5 I

minus 2J

plus 8K and then minus

2i Plus 3j

plus 4K

5i minus 2i is going to be 3i

negative 2 J minus 3j that's negative 5j

AK minus 4K that's going to be positive

4K

so that's how you could find the

displacement vector using two position

vectors it's simply the difference

between the two as you go from A to B in

this case

so if you go to my website

video.tutor.net

it's going to take you to this page

where you can

check out my ebook

on how to pass

math and science classes

or if you want to get the first chapter

free you can join my email list

so feel free to take a look at this when

you get a chance if you're interested

but now let's get back to the video