What is a Relation? | Don't Memorise
Summary
TLDRThis script explains the concept of a relation in set theory. It uses an example with two sets, P and Q, and their Cartesian product to illustrate ordered pairs. The relation R is defined such that Q is a multiple of P, and the script demonstrates how to represent this relation using the set builder and roster methods. It also shows how to visually represent the relation with an arrow diagram, highlighting that the relation is a subset of the Cartesian product.
Takeaways
- 🔢 A relation is defined as a set of ordered pairs that satisfy a particular relationship.
- 📚 The example uses two sets, P = {2, 4} and Q = {10, 20, 35}, to demonstrate the concept.
- 🎯 The Cartesian product of sets P and Q, denoted as P x Q, results in ordered pairs where each element of P is paired with each element of Q.
- 📐 An arrow diagram is introduced to visualize the Cartesian product of sets P and Q, showing all possible ordered pairs.
- ✅ The relation R is introduced with a condition that Q must be a multiple of P, which filters the ordered pairs from the Cartesian product.
- 📝 The set builder notation is used to represent the relation R, specifying that Q is a multiple of P for each ordered pair.
- 📋 The roster method lists the ordered pairs that satisfy the relation R, such as (2, 10), (2, 20), and (4, 20).
- 📊 An arrow diagram can also represent the relation R, showing arrows for each ordered pair that meets the relation's criteria.
- 📖 The relation R is a subset of the Cartesian product P x Q, highlighting the subset of ordered pairs that satisfy the defined relationship.
- 💡 The script concludes by emphasizing that a relation provides a way to identify and represent ordered pairs that meet a specific condition.
Q & A
What is a relation in set theory?
-A relation in set theory is a set of ordered pairs that satisfy a specific relationship between elements of two sets.
How do you define the Cartesian product of two sets?
-The Cartesian product of two sets P and Q is a set of ordered pairs (P, Q) where P is from set P and Q is from set Q.
What is the difference between the Cartesian product and a relation?
-The Cartesian product is a set of all possible ordered pairs between two sets, while a relation is a subset of the Cartesian product that satisfies a specific condition.
Can you provide an example of sets P and Q from the transcript?
-Yes, in the transcript, set P has elements {2, 4} and set Q has elements {10, 20, 35}.
How many ordered pairs are there in the Cartesian product of sets P and Q from the example?
-There are six ordered pairs in the Cartesian product of sets P and Q: (2,10), (2,20), (2,35), (4,10), (4,20), (4,35).
What is the relation R- introduced in the transcript?
-The relation R- is defined such that Q is a multiple of P, meaning only ordered pairs where the second element is a multiple of the first are included.
What is the set builder notation and how is it used to represent a relation?
-Set builder notation is a way to describe a set by stating the properties that its members must satisfy. For a relation, it is used to represent all ordered pairs that satisfy the relation's condition.
What is the roster method mentioned in the transcript?
-The roster method is a way to represent a set by listing all its elements explicitly, like in a roster. For a relation, it lists all ordered pairs that satisfy the relation.
How many ordered pairs satisfy the relation R- in the given example?
-In the example, the ordered pairs that satisfy the relation R- are (2,10), (2,20), and (4,20), as these are the pairs where Q is a multiple of P.
What does it mean for a set to be a subset of the Cartesian product?
-A set being a subset of the Cartesian product means that it consists only of the ordered pairs from the Cartesian product that meet certain criteria, in this case, the relation R-.
How is a relation visually represented using an arrow diagram?
-In an arrow diagram, an arrow is drawn from each element of set P to each element of set Q that satisfies the relation. This visually represents the ordered pairs in the relation.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Types of Set | Sets || Mathematics in the Modern World
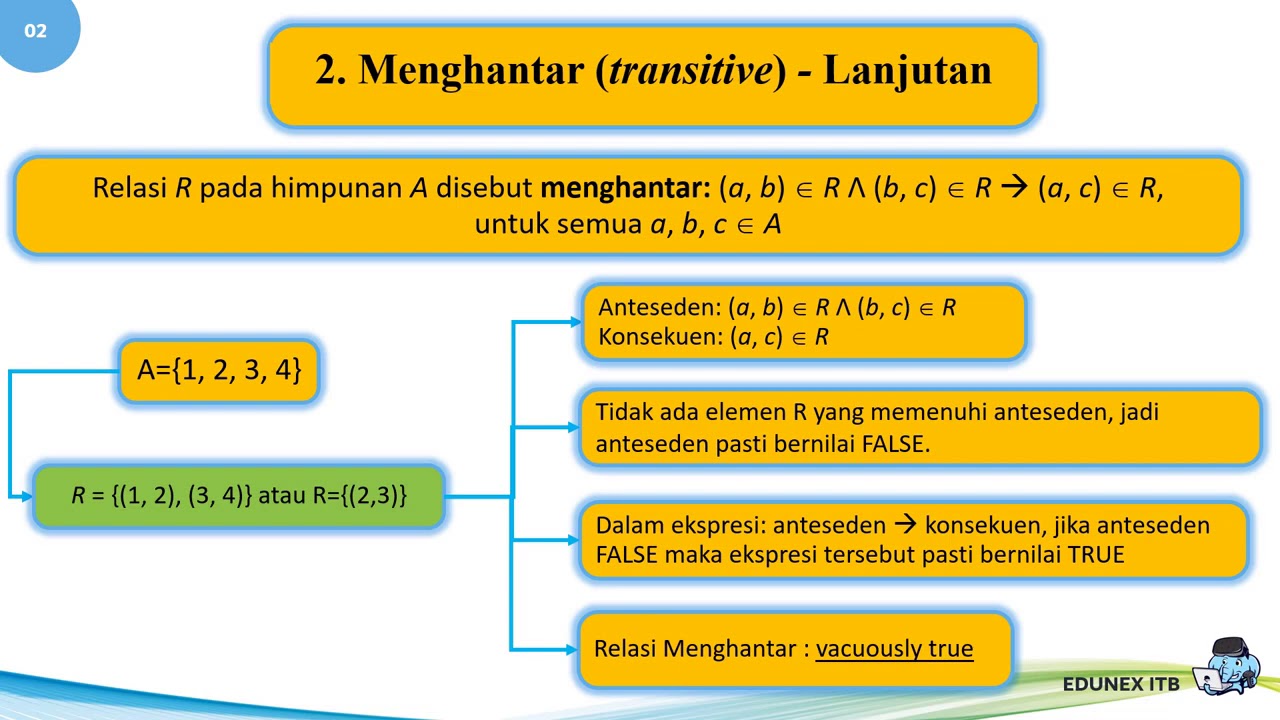
Matdis 06 : Relasi&Fungsi (Segmen 3: sifat-sifat relasi)

Corso zero di matematica (lezione 2) - Funzioni tra insiemi

Types of sets

Bab 4 (part 1) Matematik Tingkatan 4 KSSM: 4.1 Persilangan set
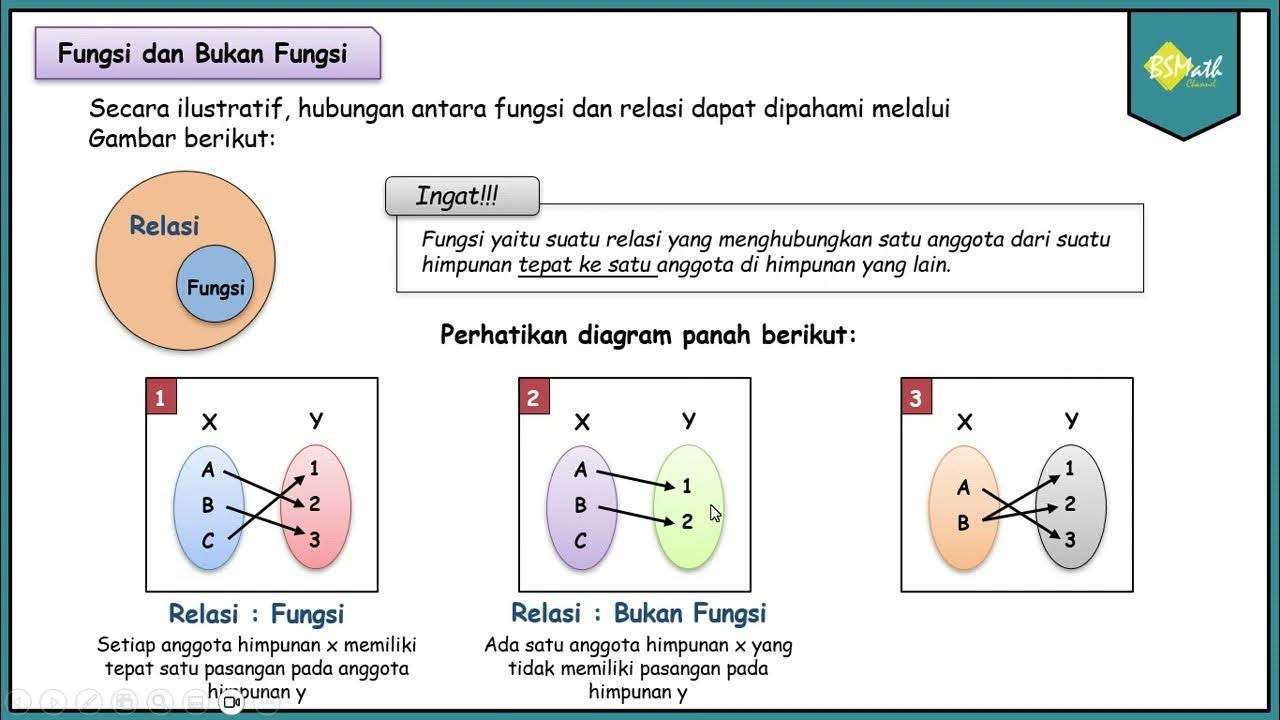
Pengertian Fungsi - Matematika Kelas XI Kurikulum Merdeka
5.0 / 5 (0 votes)