Reconstruction of a Signal Using Practical LPF

Summary

In this lecture, the concept of signal recovery using practical and ideal low-pass filters is discussed, with a focus on critical sampling. The lecturer explains that while an ideal low-pass filter can recover a signal when the sampling frequency is twice the maximum message frequency, a practical low-pass filter introduces limitations due to the transition band. This results in incomplete recovery of the message signal. The lecture concludes that signal recovery under critical sampling conditions with a practical low-pass filter is not possible, and includes a homework question on the optimal sampling mode.

Takeaways

• 🔧 The lecture focuses on using a practical low-pass filter to recover a message signal under critical sampling conditions.
• 📐 Critical sampling occurs when the sampling frequency (Omega s) equals twice the maximum frequency component of the message signal (Omega M).
• 🎯 Ideal low-pass filters can successfully recover a message signal if the critical frequency equals the maximum frequency component of the message signal.
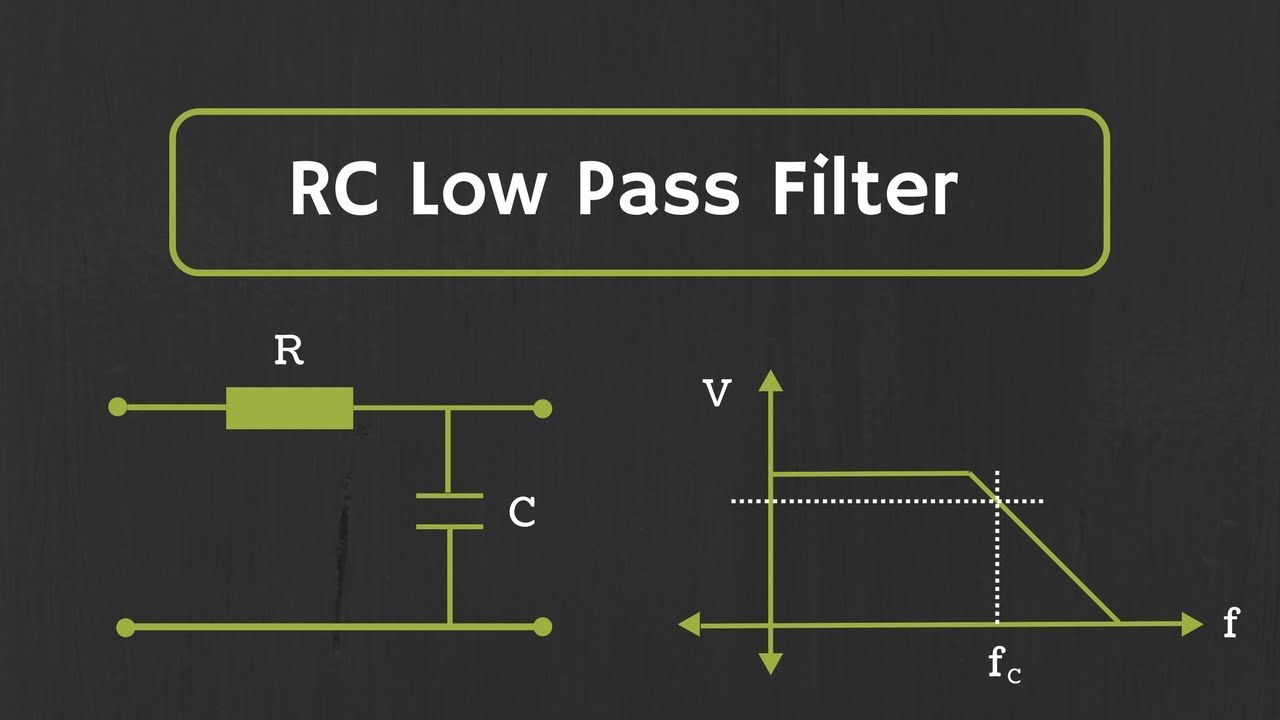
• 🎛️ Practical low-pass filters, unlike ideal filters, have a gradual transition from pass band to stop band, which introduces a transition band.
• 📉 In the case of practical low-pass filters, some unwanted portions of the sampled signal are passed along with the desired signal, leading to signal distortion.
• 🚫 With practical low-pass filters, it is not possible to perfectly recover the message signal in critical sampling conditions.
• ✅ The lecture concludes that option B (false) is correct: recovery is not possible using a practical low-pass filter when Omega s is twice Omega M.
• 📊 The Fourier transform is essential in analyzing the input signal and determining whether the recovered signal matches the original message signal.
• 🧠 For homework, students are asked to determine which sampling mode should be used with a practical low-pass filter: critical sampling, undersampling, or oversampling.
• 📎 The importance of understanding the frequency response of practical filters, as it impacts the ability to recover the original signal, is emphasized.

Q & A

What is the primary focus of the current lecture?

The primary focus is on determining whether the message signal can be recovered using a practical low-pass filter when the sampling frequency (Omega s) is equal to twice the maximum frequency component of the message signal (Omega M).

What is critical sampling, and how is it defined?

Critical sampling occurs when the sampling frequency (Omega s) is exactly twice the maximum frequency component (Omega M) of the message signal. Under this condition, the spectrums of the signal touch each other.

What are the key differences between an ideal and a practical low-pass filter?

An ideal low-pass filter has a sharp cutoff between pass band and stop band, while a practical low-pass filter has a transition band where the transition from pass to stop band is gradual rather than instantaneous.

What is the role of the pass band in a low-pass filter?

The pass band is the frequency range between -Omega C and Omega C, where the low-pass filter allows the signal to pass through. Only the signal components within this frequency range appear at the output.

What happens in the stop band of a low-pass filter?

In the stop band, the low-pass filter blocks the input signal, meaning any signal components with frequencies greater than Omega C are not passed to the output.

Why is it important to match the cutoff frequency (Omega C) to the maximum frequency component (Omega M) in the ideal filter case?

When the cutoff frequency (Omega C) is equal to the maximum frequency component of the message signal (Omega M), the signal can be perfectly recovered, as the entire message signal spectrum falls within the pass band.

Can the message signal be perfectly recovered using a practical low-pass filter under critical sampling?

No, the message signal cannot be perfectly recovered using a practical low-pass filter under critical sampling because the transition band of the filter causes additional unwanted components to pass through, leading to distortion.

What is the effect of the transition band in a practical low-pass filter?

The transition band causes some components outside the desired pass band to pass through, leading to incomplete signal recovery and distortion in the recovered signal.

Why is the answer to the question in the lecture 'false'?

The answer is 'false' because with a practical low-pass filter, the message signal cannot be fully recovered under the condition Omega s = 2 * Omega M, due to the presence of the transition band in the filter's response.

What homework question is posed at the end of the lecture?

The homework question asks which sampling mode should be used with a practical low-pass filter: (a) critical sampling, (b) under-sampling, or (c) over-sampling. Students are encouraged to post their answers in the comments, along with any relevant conditions.

Outlines

00:00

🔧 Introduction to Signal Reconstruction with Practical Low-Pass Filters

This paragraph introduces the transition from ideal to practical low-pass filters in signal reconstruction. It outlines the objective of the lecture, which is to determine whether a practical low-pass filter can recover the message signal under the condition that the sampling frequency (Omega s) is equal to twice the maximum frequency component (Omega M) of the message signal. The paragraph explains the concept of critical sampling and emphasizes the differences between ideal and practical low-pass filters.

05:04

🔍 Understanding the Pass Band and Stop Band of Low-Pass Filters

The second paragraph delves into the concepts of pass band and stop band in low-pass filters. It explains how a low-pass filter only passes signal components within a certain frequency range (pass band) and blocks components outside this range (stop band). This detailed description clarifies how the frequency response of a practical low-pass filter works and how these frequency bands impact the signal reconstruction process.

10:08

📉 Fourier Transform and Signal Recovery

This paragraph focuses on how the input signal’s Fourier transform interacts with the frequency response of a low-pass filter. It explains the process of obtaining the recovered message signal by multiplying the Fourier transform of the input signal with the filter’s frequency response. The explanation emphasizes how this process leads to the recovered signal, which may or may not match the original message signal depending on certain conditions.

⚖️ Critical Sampling with an Ideal Low-Pass Filter

Here, the lecture explores the case of critical sampling with an ideal low-pass filter. By explaining the multiplication of the frequency response (H Omega) with the signal’s Fourier transform (S Omega), the paragraph demonstrates that when the cutoff frequency equals the maximum frequency of the message signal, the signal is perfectly recovered. It concludes that under these conditions, the recovered message signal is identical to the original.

❌ Practical Low-Pass Filter and Signal Recovery Challenges

This paragraph explains why signal recovery fails when using a practical low-pass filter with critical sampling. It highlights the existence of a transition band in practical filters, which causes additional unwanted signal components to pass through. This results in an imperfectly recovered signal that does not match the original message signal. As a result, the lecture concludes that signal recovery is not possible under these conditions.

📚 Homework: Exploring Sampling Modes with Practical Filters

The final paragraph presents a homework assignment. It challenges the reader to determine the appropriate sampling mode when using a practical low-pass filter. The three options given are critical sampling, undersampling, and oversampling. Students are encouraged to post their answers in the comments, along with any conditions that apply to their choice.

Keywords

💡Low-pass filter

A low-pass filter is a device or process that allows signals with a frequency lower than a certain cutoff frequency to pass through while attenuating higher frequencies. In the video, the speaker contrasts practical and ideal low-pass filters, focusing on how the practical version introduces challenges in signal recovery due to its less sharp transition between pass and stop bands.

💡Practical low-pass filter

A practical low-pass filter refers to a real-world filter that has a gradual transition between its pass band and stop band, unlike an ideal low-pass filter with a perfect cutoff. This practical filter has a 'transition band,' making it more difficult to fully recover signals in some scenarios. The video uses this concept to explain why signal recovery is more challenging when using practical filters in critical sampling conditions.

💡Ideal low-pass filter

An ideal low-pass filter has a perfectly sharp cutoff frequency, meaning it passes all frequencies below the cutoff and blocks all frequencies above it. The speaker mentions that in previous lectures, the ideal low-pass filter was used to recover signals effectively, but in real-world scenarios, practical filters are used, which complicates the recovery process.

💡Omega s

Omega s (Ωs) is the sampling frequency in the context of signal processing. It is the rate at which a continuous signal is sampled to create a discrete signal. The video discusses a condition where Omega s equals twice the maximum frequency component of the message signal, known as critical sampling, and explains the challenges of signal recovery in this case.

💡Omega M

Omega M (ΩM) refers to the maximum frequency component of the message signal in the discussion of sampling theory. The video explores the relationship between Omega M and Omega s (sampling frequency) and shows how signal recovery is possible when the cutoff frequency (Omega C) matches Omega M in the ideal low-pass filter case.

💡Critical sampling

Critical sampling occurs when the sampling frequency (Ωs) is exactly twice the maximum frequency component of the message signal (ΩM). This is a key concept in the video, as it explores how signal recovery can fail when using practical low-pass filters under this condition due to the overlap of spectral components in the transition band.

💡Pass band

The pass band is the range of frequencies that a filter allows to pass through without attenuation. In the video, the pass band is discussed in relation to both ideal and practical low-pass filters, with the ideal filter having a sharp cutoff and the practical filter having a gradual transition. The speaker emphasizes how the pass band affects the recovery of the message signal.

💡Stop band

The stop band is the range of frequencies that a filter blocks or attenuates significantly. In the video, the stop band is discussed in relation to both ideal and practical low-pass filters, where the practical filter’s stop band is less sharply defined, causing additional parts of the sampled signal to be mistakenly passed, making signal recovery less accurate.

💡Transition band

The transition band is the range between the pass band and the stop band in a practical low-pass filter, where the filter gradually attenuates the signal. In the video, this concept is crucial for understanding why practical low-pass filters are less effective at recovering signals in critical sampling cases, as some unwanted spectral components pass through during this transition.

💡Fourier transform

A Fourier transform is a mathematical operation that transforms a signal from the time domain to the frequency domain. The video explains how the Fourier transform of the input signal (denoted as S(Ω)) is multiplied by the frequency response of the filter (H(Ω)) to analyze the output signal. This process is key to understanding how filters affect signal recovery in different scenarios.

Highlights

Reconstruction of signals using a low-pass filter, differentiating between ideal and practical filters.

Introduction to critical sampling: when sampling frequency is twice the maximum frequency component.

Explanation of pass band in a low-pass filter, which passes the portion of input signals between the cutoff frequencies.

Explanation of stop band, where the input signal frequencies are stopped by the filter when they exceed the cutoff frequency.

Process of recovering message signals using an ideal low-pass filter and how it relates to sampling.

The importance of matching the critical frequency with the maximum frequency component of the message signal for successful recovery.

Fourier transform of the input signal and how it interacts with the filter's frequency response to recover the signal.

Ideal low-pass filter successfully recovers the message signal when the critical frequency equals the maximum frequency.

Discussion of practical low-pass filters: differences in frequency response compared to ideal filters.

Introduction of the transition band in practical low-pass filters, which affects signal recovery.

In critical sampling with practical low-pass filters, parts of the spectrum that shouldn't be passed are passed due to the transition band.

Conclusion: Recovery of the original message signal is not possible with a practical low-pass filter under critical sampling conditions.

Answer to the question: the correct option is 'false' for recovering signals under critical sampling with a practical low-pass filter.

Homework problem posed: determining which sampling mode (critical, under, or over) should be used with a practical low-pass filter.

Instructions to submit the answer to the homework problem in the comments, with any conditions if applicable.

Transcripts

in the last lecture we saw how to

reconstruct his signal using a low-pass

filter and in this lecture we will try

to answer a question according to the

question who with practical low-pass

filter can we recover the message signal

when Omega s is equal to twice of Omega

M there are two options a is true and B

is false so from the question it is

clear that we are using a practical

low-pass filter and in the previous

lecture we used an ideal low-pass filter

so instead of ideal low-pass filter we

will use the practical low-pass filter

and therefore we must have the knowledge

of frequency response of the practical

low-pass filter and then we need to

focus on this condition Omega s is equal

to twice of Omega M this means sampling

frequency is equal to two times the

maximum frequency component of the

message signal and we know under this

condition the waveform of s Omega will

look like this the spectrums will be

touching each other and this particular

condition is known as condition of

critical sampling critical sampling so

we are having the condition of critical

sampling and we are using practical

low-pass filter

to recover this signal so let's try to

understand if we can recover the signal

in this condition or not in the previous

lecture we saw that the frequency

response H Omega of a practical low-pass

filter will look like this this

frequency here is equal to Omega C which

is the cutoff frequency this frequency

here is equal to minus Omega C and from

minus Omega C to Omega C we call this

pass band we call this pass band and we

are calling it pass band

because when you apply a signal to a

low-pass filter then this signal who

will be reflected at the output only

with the portion between minus Omega C 2

plus Omega C this means the portion of

the input signal between these two

frequencies is passed by the low-pass

filter and therefore we call this pass

band and now we will talk about this top

band stop band is the band of

frequencies for which the low pass

filter we are using will stop the input

signal and it is stopping the input

signal because you can see that the

frequency response of the low pass

filter we are having is equal to zero

when Omega is greater than Omega C so we

call this band of frequencies stop band

and we are calling it stop band because

corresponding to these band of

frequencies the input signal will not

appear at the output that is it is

stopped by the low-pass filter and we

know we use low pass filter to recover

the message signal we obtain the sampled

signal St after performing the sampling

and then we feed this sample signal to a

low-pass filter in our case we are

having the ideal low-pass filter we are

having the ideal low-pass filter and the

output of the low pass filter we call as

recovered message signal so we

represented by M R T now this recovered

message signal may or may not be equal

to the original message signal there are

some conditions which we have discussed

in great detail in the previous lecture

and we know the Fourier transform of the

input signal s T is has Omega and here

you can see the Fourier transform and

the low pass filter we are having which

is ideal in nature is having the

frequency response like this so the

ideal low-pass filter we are having

he is having the frequency response like

this and we have the knowledge of s

Omega and H Omega this means we have the

knowledge of input signals Fourier

transform and the systems frequency

response so if we multiply them we will

get the output signals Fourier transform

mr Omega and if we have Hammar Omega we

can perform the inverse Fourier

transform to get MRT now this MRT may or

may not be equal to the message signal

it depends on various factors now let's

try to understand whether we can have

the recovered signal same as the message

signal when there is critical sampling

along with the ideal low-pass filter

used so we will multiply H Omega and has

Omega and to give you the clear picture

of what actually is happening I will

copy this portion of the waveform and

then I will paste it and finally I will

try to overlay it properly here and now

you can see that according to the

property of low pass filter this portion

of the waveform of s Omega will be

passed and this portion and this portion

will be stopped by the low-pass filter

and therefore M high Omega will have the

waveform like this which is the spectrum

of the message signal the Fourier

transform of the message signal is

having the waveform like this as we have

seen in the first lecture of the

sampling theorem therefore here we can

see that when Omega C is equal to Omega

M we know this frequency here is equal

to Omega M this is twice of Omega M so

here you can see that Omega C the

critical frequency is equal to Omega M

and when this happens we are easily

getting our signal back because M R

Omega we are getting is same as M Omega

and therefore when we recover the

message signal

it will be same as the original message

signal MT so I hope this case is clear

to you that what we are required to do

when there is ideal low-pass filter in

the critical sampling case we are

required to keep our critical frequency

equal to maximum frequency component of

the message signal and when this happens

we can easily extract our signal back

but the question is asking about the

practical low-pass filter it is not

asking about the ideal low-pass filter

so let's move on to the question now we

will understand what will happen when

there is practical low-pass filter in

the case of critical sampling and forced

we will have a look at the frequency

response of the practical low-pass

filter the frequency response H Omega

will look like this and here you can see

that the transition from pass band to

stop band is not this sharp it is taking

some time and therefore here in this

case we are having one more band which

is known as transition band from here to

here we know it is pass band and from

here to here this portion is known as

transition band so there is transition

band and because of transition band this

top band will start from here so this is

our stop band and now we will follow the

same process we will feed our sampled

signal to the practical low-pass filter

and then we will try to obtain M R Omega

and from M R Omega we will obtain M R T

so let's quickly copy this portion of

the waveform and we will try to overlaid

like we have done in the previous case

and now you can see that now you can

clearly see that this portion of the

waveform is passed which is the spectrum

of the message signal

and we need only this portion but along

with this portion this portion and this

portion of these two spectrums are also

passed by the practical low-pass filter

and therefore M R Omega will not be

equal to M Omega and therefore the

obtained or recovered message signal

will not be equal to the message signal

so whenever you have the critical

sampling case in which Omega s is equal

to twice of Omega M and you are using a

practical low-pass filter then the

recovery is not possible so this is the

answer of the question the answer is

false

we cannot recover the message signal

when Omega s is equal to twice of Omega

M with a practical low-pass filter so

option B is the correct option which is

false

now there is one homework problem and in

this homework problem you need to tell

me with a practical low-pass filter

which sampling mode should we use option

is critical sampling option B's under

sampling and option C's over sampling so

try to answer this question and once you

have your answer post it in comment

section and if there is any condition

along with your answer then also mention

that condition so this is all for this

lecture see you in the next one

[Applause]

[Music]