ALL OF GRADE 11 MATH IN 1 HOUR! (exam review part 1) | jensenmath.ca

Summary

This script is a comprehensive review for a grade 11 functions math course, covering key topics like identifying functions using the vertical line test, stating domains and ranges, and function notation. It delves into quadratic functions, explaining how to find vertices through completing the square and partial factoring, and solving quadratics by factoring, using the quadratic formula, and solving linear-quadratic systems. The video also touches on simplifying and subtracting rational expressions, emphasizing the importance of factoring and stating restrictions to avoid undefined expressions.

Takeaways

• 📚 The video is a review for grade 11 functions math, covering main topics and exam expectations.
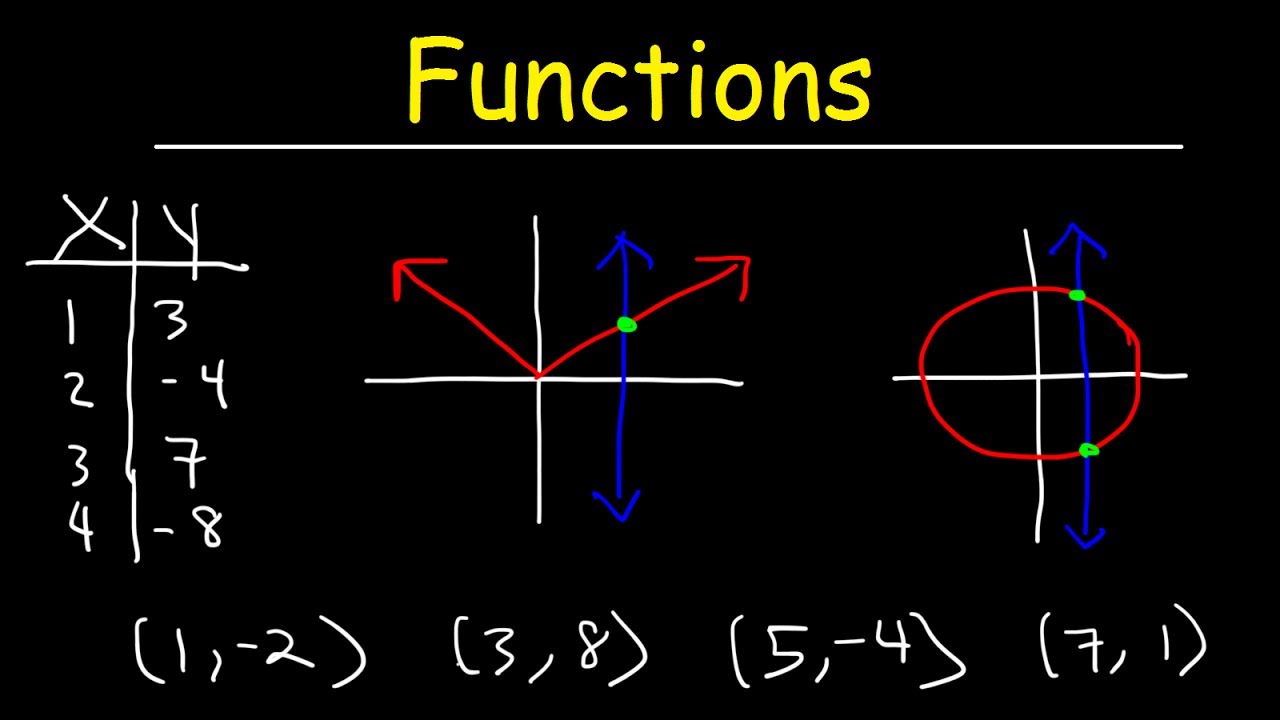
• 🔍 It discusses how to determine if a relation is a function using the vertical line test.
• 📈 The script explains how to define the domain and range of a relation, with examples.
• 📝 Function notation is introduced, replacing 'y' with 'f(x)' to represent the y-value of a function at a given x.
• 🔢 Techniques for finding the vertex of a quadratic function are reviewed, including completing the square and partial factoring.
• 📉 Methods for solving quadratic equations are detailed, such as factoring and using the quadratic formula.
• 🤝 The script covers how to solve systems of linear and quadratic equations, including substitution and factoring.
• ✅ It emphasizes the importance of stating restrictions when simplifying rational expressions to avoid undefined values.
• 🧮 Tips for subtracting rational expressions are provided, highlighting the need for common denominators and fully factored expressions.
• 📊 The video concludes with a quick overview of rational expressions, including simplification and stating restrictions.

Q & A

What is the primary condition for a relation to be considered a function?

A relation is considered a function if each value in the domain corresponds to exactly one value in the range, passing the vertical line test.

How do you perform the vertical line test to determine if a relation is a function?

You draw a vertical line anywhere on the graph of the relation and check if it intersects the graph at more than one point. If it does, the relation fails the test and is not a function.

Can you explain how to determine the domain and range of a relation?

The domain is the set of all possible x-values the relation can take, while the range is the set of all possible y-values. You determine the domain by looking at the horizontal extent of the relation and the range by looking at the vertical extent.

What is function notation and how is it used?

Function notation, such as f(x), is a way to represent a function where 'f' is the function name and 'x' is the input. It replaces y in the equation y = ... and is used to find the y-value (output) for a given x-value (input).

Describe the process of completing the square to find the vertex of a quadratic function.

Completing the square involves rewriting the quadratic equation in vertex form by factoring a perfect square trinomial and adjusting the constant term to maintain equality, which reveals the vertex of the parabola.

How do you find the vertex of a quadratic function using partial factoring?

Partial factoring involves setting the quadratic equation equal to a known y-intercept and solving for x-values that yield this y-intercept. The vertex's x-coordinate is the average of these x-values.

What are the different methods to solve quadratic equations discussed in the script?

The script discusses completing the square, partial factoring, factoring by grouping, and using the quadratic formula as methods to solve quadratic equations.

How does the discriminant affect the number of solutions when solving a quadratic equation?

The discriminant (b^2 - 4ac) determines the nature of the solutions: a positive discriminant results in two distinct real solutions, zero gives one real solution (a repeated root), and a negative discriminant results in no real solutions (two complex solutions).

What is the significance of the discriminant when solving a linear-quadratic system?

The discriminant's value dictates the number of intersection points (solutions) between the line and the parabola: two points for a positive discriminant, one point for a zero discriminant (tangent line), and no intersection points for a negative discriminant.

How do you simplify rational expressions, and what are the key steps involved?

To simplify rational expressions, you factor the numerator and denominator, then cancel out common factors. Key steps include changing division to multiplication, factoring, and reducing by canceling common factors across the numerator and denominator.

When subtracting rational expressions, what is the first step you should take?

The first step when subtracting rational expressions is to ensure both expressions have a common denominator, which may involve factoring each expression fully.

Outlines

00:00

📚 Introduction to Functions Course Review

This paragraph introduces a review video for a grade 11 functions math course. The speaker plans to provide an overview of the main topics covered in the course, including what constitutes a function, how to determine if a relation is a function using the vertical line test, and how to state the domain and range of a relation. The speaker also mentions that more in-depth videos can be found on Jensen Mascot CA for those seeking further explanations.

05:01

🔍 Deep Dive into Quadratics and Vertex Finding

The speaker discusses the properties of quadratic functions, focusing on how the value of 'a' affects the direction in which the parabola opens. They explain two methods for finding the vertex of a parabola: completing the square and partial factoring. Completing the square involves transforming the standard form of a quadratic equation into vertex form to easily identify the vertex coordinates. Partial factoring involves setting the quadratic equation to its y-intercept value and solving for the x-values where the y-coordinate is the same, then averaging to find the vertex.

10:01

🔢 Solving Quadratics Through Factoring and the Quadratic Formula

This section covers two methods for solving quadratic equations: factoring and using the quadratic formula. Factoring is applicable when the leading coefficient (a) is 1, allowing for easy identification of factors. When a is not 1, factoring requires grouping and finding two numbers that meet specific product and sum criteria. The quadratic formula, applicable to all quadratics, is demonstrated with an example where the formula is used to find the exact x-intercepts by simplifying the square root of the discriminant.

15:02

🤝 Solving Systems of Linear and Quadratic Equations

The paragraph explains how to solve a system of linear and quadratic equations, which involves finding the points of intersection between a parabola and a line. The speaker outlines the possibility of obtaining two solutions (secant line), one solution (tangent line), or no solutions at all, depending on the discriminant's value. The method of substitution is used to solve the system, where the y-values from both equations are equated, and the resulting equation is solved for x. The x-values are then substituted back into the original equations to find the corresponding y-values, yielding the points of intersection.

20:04

📉 Simplifying and Subtracting Rational Expressions

This section teaches how to simplify and subtract rational expressions. For division, the process involves changing the division to multiplication, factoring both the numerator and the denominator, and then reducing by canceling common factors. For subtraction, a common denominator is necessary, which is found after fully factoring both the numerator and the denominator. The speaker emphasizes the importance of fully factoring before attempting to reduce and provides examples of both operations, including stating the restrictions on x-values that would make the denominator zero.

25:05

📐 Further Exploration in Rational Expressions

The final paragraph continues the discussion on rational expressions, focusing on the subtraction of such expressions. The speaker emphasizes the need to fully factor both the numerator and the denominator before finding a common denominator. They provide a detailed example of subtracting two rational expressions, showing the process of expanding and simplifying the numerator, and then checking for further reduction after ensuring the numerator and denominator are fully factored. The importance of stating restrictions based on the values of x that would result in a zero denominator is reiterated.

Keywords

💡Function

A function in mathematics is a relation where each input (or 'x' value) is associated with exactly one output (or 'y' value). This concept is central to the video's theme as it sets the foundation for understanding more complex mathematical relationships. The video explains that a function can be identified by passing the vertical line test, where a vertical line drawn through a graph will touch no more than one point if the graph represents a function.

💡Domain

The domain of a function refers to the set of all possible input values (x-values) for which the function is defined. In the video, the domain is illustrated by tracing a point horizontally along a graph to determine the range of x-values the function can take, often represented as 'x is an element of real numbers' with certain restrictions.

💡Range

The range of a function is the set of all possible output values (y-values) that result from the function. The video describes how to determine the range by tracing a point vertically along the graph, noting where it can go without restriction, often represented as 'y is an element of real numbers' with or without certain minimum or maximum values.

💡Function Notation

Function notation, such as 'f(x)', is a way to express a function where 'f' denotes the function and 'x' is the input. The video emphasizes the shift from using 'y =' to 'f(x)' to denote the output of a function for a given input. This notation simplifies the process of evaluating functions and is used throughout the script to demonstrate how to find specific function values.

💡Quadratic

A quadratic function is a type of function with a parabolic graph, represented by an equation of the form ax^2 + bx + c. The video discusses various methods for dealing with quadratics, including finding their vertex and solving them by factoring or using the quadratic formula. Quadratics are a key concept in the video as they represent a fundamental type of function studied in algebra.

💡Vertex

The vertex of a parabola, which is the graph of a quadratic function, is the point where the parabola reaches its minimum or maximum value. The video explains how to find the vertex using methods like completing the square or partial factoring. The vertex is significant as it gives insight into the behavior of the function and is a key point in the graph.

💡Factoring

Factoring is the process of breaking down a polynomial into a product of its factors. The video covers different scenarios of factoring quadratics, including when the 'a' value is one and when it is not, leading to different methods of factoring. Factoring is essential for solving quadratic equations and finding x-intercepts.

💡Quadratic Formula

The quadratic formula is a method for finding the solutions to a quadratic equation and is presented as a universal solution method in the video. It is given by the formula -b ± √(b²-4ac) / (2a). The video demonstrates how to apply this formula to find x-intercepts of a parabola, even when the equation cannot be easily factored.

💡Linear-Quadratic System

A linear-quadratic system refers to the intersection points of a linear equation (a straight line) and a quadratic equation (a parabola). The video discusses solving such systems using substitution to find the points of intersection, which could be zero, one, or two depending on the relationship between the line and the parabola.

💡Rational Expressions

Rational expressions are fractions where the numerator and the denominator are polynomials. The video covers how to simplify rational expressions by finding common denominators and reducing fractions. It also demonstrates how to subtract rational expressions by ensuring the expressions have a common denominator, which is a crucial skill for working with algebraic fractions.

Highlights

Overview of main topics in grade 11 functions math course

Explanation of what makes a relation a function

Demonstration of the vertical line test for functions

How to state the domain and range of a relation

Introduction to function notation using f(x) instead of y

Methods for finding the vertex of a quadratic function

Completing the square to convert a quadratic into vertex form

Partial factoring as an alternative method to find the vertex

Solving quadratics by factoring when the leading coefficient is one

Solving quadratics by factoring when the leading coefficient is not one

Using the quadratic formula for solving non-factorable quadratics

Simplification of radical expressions in quadratic solutions

Solving a linear-quadratic system using substitution

Handling different outcomes of linear-quadratic system solutions

Simplifying rational expressions by changing division to multiplication

Cross-reducing rational expressions after multiplication

Subtracting rational expressions and finding a common denominator

Factoring and simplifying the numerator in rational expression subtraction

Stating restrictions for rational expressions to avoid undefined values

Transcripts

just a quick exam review video for the

grade 11 functions math course I'm just

going to do a quick overview of the main

topics you would do in a functions

course and topics that you could

probably expect to see on your exam

if you want more in-depth videos with

explanations of each individual section

make sure you go to Jensen mascot CA and

check out the videos there for more

detailed explanations so let's just go a

brief overview really quickly I'm going

to try and fit this all into an hour if

I can and I'll break it up into parts

for you let's just get right into it so

in the functions course the first thing

you probably would have learned about is

what makes a relation a function so

basically each value in the domain of a

relation can only correspond to one

value in the range so each value of x so

if each X can only have one

corresponding value of y if it's a

function and what you would have done is

the vertical line test to check that you

would have checked different relation

passes or fails the vertical line test

and that tells you whether it's a

function or not so here's an example of

a relation that fails the vertical line

test so if you take a vertical line and

you drag it horizontally across a

relation if it ever touches the relation

in more than one spot then it fails the

vertical line test and it is not a

function this one is not a function

because for an x value of negative six

there are two possible Y values negative

2 4 so there's more than one y value

that corresponds to a value of x so it's

not a function fails the vertical line

test this is a relation that passes the

vertical line test if I drag a vertical

line across this horizontally it never

touches the relation in more than one

spot at a time therefore this relation

is a function this one is a function

next thing you would have learned is how

to state the domain and the range of a

relation so domain is basically what

values of X can the relation take so

that's basically looking at where

horizontally if I were to drag this

point along the relation and keep in

mind these arrows tell us it extends

forever to the left so if I were to drag

this point along the relation where

horizontally did this point go so the

furthest right it goes is here and every

went further than three

and then it would go forever to the left

so if I orifice states a domain of this

function this is how we write it I would

say X is an element of real numbers

given that the x value

it never was bigger than three it was

always at three or less it was always

less than or equal to three

what about the range so the range is

looking at where did the point go

vertically so if you think back to when

I was tracing this point along the

relation where did it go vertically keep

in mind if this graph was extended it

would go forever up and forever down

there's no restrictions on how high or

how low that point would go if we

continued that graph forever so we would

just say Y is an element of real numbers

there's no restrictions on how high or

how low that point can go let's look at

this relation over here so as I'm

tracing this point along this relation

the domain where is this point going

horizontally and keep in mind if this

graph extended forever if it kept going

and going and going going there would be

no restrictions on how far left or right

that point could go so it would go

forever to the right forever to the left

we'd say the domain there's no

restrictions X is an element of real

numbers it could be any real number but

for the range notice as I'm tracing this

point we're vertically is this point

going it never goes below this point

right here that's the minimum point

negative one it goes forever up but it

never goes below that point so for our

range Y is an element of real numbers

but there's a restriction y is in

element of real numbers given that

that's what the vertical line means it's

always at or above negative one so

greater than or equal to negative one so

that's how we States the main and range

next you have looked at what's function

notation so in previous math courses you

would write equations like this y equals

and then your relation what we want to

do now is use a new notation instead of

writing Y we write f of X it means the

same thing this means the Y value of the

function at a given x value so these two

equations that are written here are

equivalent ways of writing the same

thing it's just we use this note

here we write f of X instead of writing

y this means the Y value of the function

at a given value of x so if I wanted to

figure out the Y value when X is

negative 3 we'd write it like this F at

negative 3 the value of the function

when X is negative 3 and then what you

would do is plug into the equation

negative 3 for X and then evaluate and

if we evaluated this negative 3 plus 3

is 0 0 square root of 0 times 3 point 5

0 minus 1 negative 1 what we have

figured out when X is negative 3 y is

negative 1 so on the graph of the

function you would find the point

negative 3 negative 1 next if you

remember quadratics quadratic the graph

of quadratic forms a parabola either one

that opens up or one that opens down

depending on what your a value is so

this a value bigger than zero so we know

it opens up so we know we have a problem

looks like this which means the vertex

this little point here is going to be a

minimum point

so I usually teach my class at least a

couple different methods for finding the

vertex let me review a couple of them

with you right now first of which is

completing the square so it's basically

taking this standard form quadratic this

ax squared plus BX plus C quadratic and

changing it into vertex form because if

we change it to vertex form the h and

the K tell us exactly what the vertex of

the quadratic is going to be so to get

the standard form to look like the

vertex form there's a bunch of steps we

go through first step is that we put

brackets around the first two terms and

leave the third term the y-intercept

that plus 1 off at the end and the next

thing that we do is we factor out what's

in front of the x squared

don't factor out an X just take it

what's in front of the x squared so take

out the 4 and divide both of the first

two terms by the four so we're factoring

four just from the first two terms so x

squared minus 2x plus one next what we

want to do is in the brackets here we

want to create a perfect square

trinomial by adding and subtracting

strategically half of that number

squared so half of 2 is 1 and 1 squared

is 1 we add and subtract 1 we don't

actually want this negative 1 here I

mean we're allowed to do this right

because plus 1 minus 1 is essentially 0

so we're not changing the value of our

equation at all we don't really want

that minus 1 so what we do is we take it

out by multiplying it by the coefficient

the 4 that's out front and then if we do

that what we're left with in the

brackets is just our perfect square

trinomial x squared minus 2x plus 1 and

outside of the brackets 4 times negative

1 is negative 4 and there's still that

plus 1 and off at the end and our last

step is to factor that perfect square

trinomial factor it by finding the

numbers that multiply to one add to

negative 2 and the numbers are negative

1 and negative 1 negative 1 times

negative 1 is 1 negative 1 plus negative

1 is negative 2 so it factors to X minus

1 times X minus 1 which we could just

rewrite as X minus 1 squared and

negative 4 plus 1 is negative 3 notice

how this is now in vertex form and I

told you that the vertex of this is

equal to the h and the K from the vertex

form equation so our vertex is 1

negative 3 there's another method for

finding the vertex called partial

factoring so if you remember our

standard form equation here this T value

right here this tells us the y-intercept

of the function so the y-intercept of

the function is 1 it means it crosses

the y axis around here somewhere

and we know it opens up so roughly we

would know the parabola something like

this we know it has a y-value of 1 at on

the y axis right the Winer y-intercept

is that one so that point there we know

is point 0 1 what we're going to do is

we're going to use method of partial

factoring to find another point point

something

one we're going to find another point

that has the same y value and then use

the property that parabolas are

symmetrical adds a zero plus that's

unknown x value to figure out where the

vertex is so this is how it works we set

the equation equal to three set the

original equation equal to the

y-intercept so the y-intercept is 1 so

we set equal to 1 or x squared minus 8x

Plus once we set it equal to 1 and then

salt so we're finding for what X values

have a y-coordinate of 1 so we know one

of our answers should be 0 we should get

0 and then we're going to find the other

answer average them and they'll tell us

where our vertex is so we can now move

this plus 1 to the other side and we get

0 for x squared minus 8x so a lot of

people will skip to this step and

essentially just think about like

erasing your C value and then solving

for x and to solve for X now we can come

and factor this so we can call my factor

at a 4 and an X divide both of these

terms by 4x and we get X minus Q for

this product to be 0 either factor could

be 0 so we set both factors to 0 and

then solve each separate equation divide

before 0 divided by 4 is 0 add the 2 to

the other side X could also be 2 so we

have two possible values for X we

figured out this other point here is

point 2 1 so our function is a value of

1 at 0 and that 2 so we know the vertex

is in between those so we can find the x

coordinate of the vertex just by adding

those just by averaging those two x

values so 0 plus 2 over 2 2 over 2 is 1

and we can find the y coordinate of the

vertex just by plugging that original

value of 1 back into our original

equation so 4 times 1 squared minus 8

times 1 plus 1 so 4 minus 8 is negative

4 plus 1 negative 3 so we've found once

again our vertex is 1 negative 3 so

that's just an alternate method to find

the same answer of the vertex being at 1

negative 3 so two ways of getting the

same answers next thing you would have

done with quadratics is solved by

factoring

so one where the AVA

you is one and one where it is not one

and can't be factored out so two

different methods of how you would

factor these so the first one all you

need to do is find two numbers of a

product of your C value 12 I have a sum

of your B value Sep and if we find those

two numbers those two numbers are three

and four we can go right to our factors

since the a value is one we can go right

to our factors just by adding three and

four to X and separate brackets so there

are two factors or X plus 3 and X plus 4

and if we want to actually solve this

equation that means find the

x-intercepts we know at each x-intercept

the Y value is 0 so we set the equation

to 0 and now solve this so for this

product to be 0 that means either this

factor has to be 0 or the other factor

has to be 0 to get our product to be 0

solve each equation

your first x-intercept is negative 3

your second x-intercept is negative 4 if

we want to solve this one remember

solving means find the x-intercept we

know along the x axis the y coordinate

is always 0 no matter where it crosses

we set it to 0 and now we want to solve

for what value of x makes this happen

since since our a value is not 1 it's 3

we check if we can factor it out but 3

doesn't go into 4 so we can't call and

factor it out so we're going to have to

factor this the long way by grouping we

would find two numbers with a product of

not negative 15 but of 3 times negative

15 so of negative 45 and the sum of our

B value negative 4 so the two numbers

that work for this one are negative 9

and 5 now we can't go right to our

factors for this one what we have to do

is split up the middle term since

negative 9 and 5 satisfy our product and

sum we split up the middle term into

negative 9x plus 5x and we leave our 3x

squared and our -15 and keep in mind

this is set to 0 we're allowed to do

this right because negative 9x plus 5x

is negative 4x and now what you do is

you group the first two terms together

and you put an addition sign and then

you group the last two terms together

and then you common faster each group

and always separate with an addition

side and get common factor each groups I

can take it three X's out from this

first group now we'll get X minus three

when I divide both of those by three X

common factor this group take out of

five and I would get X minus three and

what you'll notice is what's in brackets

with both of these should be the same so

since they're both the same we can

common factor out that X minus three so

if I take that out from both terms what

I'm left with is three X plus five as my

second factor now it's factored and now

what you can do is set each factor to

zero and then solve each separate

equation and those are your x-intercepts

so the first one is three the second one

if I move the plus five where it becomes

negative five then divide by three I get

negative five over three last thing

before we move on to the next section

are actually two more things if you want

to solve the quadratic that's not

factorable like this one here like we

want to solve it right set it to zero

right because the y-coordinate solving

means find the x-intercepts and at the x

intercept the y coordinate is zero so

set it to zero x squared plus six x plus

four if you're trying to solve by

factoring you'd find numbers that

multiply to four at six and the numbers

don't exist so what you have to do is

use the quadratic formula hopefully you

remember the quadratic formula negative

b plus or minus the square root of b

squared minus 4ac all over 2a and keep

in mind that the coefficient of the x

squared in this case is one so our a

value is one our be value six our C

values for let's plug all of that into

the quadratic formula and get our X

intercepts and it's good to know that

the quadratic formula always works it

works for quadratics that are factorable

as well but factoring doesn't always

work factoring only works if you can

find numbers satisfy your product and

stuff let's go ahead and use quadratic

formula so negative B so negative six

plus or minus the square root of B

squared so six

squared minus 4 a c and this all needs

to be divided by 2 a so if I I'm going

to start by evaluating the discriminant

so that's the part underneath the square

root we call that the radicand if I

evaluate that 36 minus 16 that would

give me 20 so I don't need this whole

pair here and then this is all over Q

and what we want to do is the key thing

here we want to give exact answers that

means we're not going to just evaluate

root 20 and get an approximate decimal

answer has to be rounded we want to give

an exact answer so you're going to have

to simplify this this radical expression

here root 20 so root 20 what we want to

do is we want to find

are there any perfect square numbers

right 1 Squared's 1 2 Squared's for 3

squared 9 and so on 1625 are there any

perfect square numbers that divide

evenly into root 2 1 yeah this one right

here 4 goes into 20 so I'm going to

break up root 20 into root 4 times root

5 and hopefully you'll see why in a

second so I'll break it up negative 6

plus or minus I'll break it up into root

4 times root 5 all over 2 why did I do

that well because 4 is correct square

number I can take the square root of 4

so I get negative 6 plus or minus the

square root of 4 is 2 so 2 root 5 over 2

and lastly I can simplify this I notice

I have two terms in the numerator here

they're both even so I could common

factor out a 2 from both of these so

negative 3 plus or minus 1 root 5 over 2

and now that this 2 is a factor of the

entire numerator I can simplify it with

the denominator and what I'm left with

is my first x-intercept is negative 3

plus root 5 second x-intercept negative

3 minus root 5 and those are exact

answers last thing before we move on to

the next section is solving a linear

quadratic system so that a linear

quadratic

system means you have a parabola and you

have a line and to solve it means to

find where they intersect if you get two

points of intersection we would call

that the line we call it a secant line

there's other possibilities you could

have it so your line only touches the

parabola in one spot and we call that

line a tangent line so you can only get

you could get two solutions if your the

secant line you can get one solution if

you have a tangent line or it's possible

for your line and your parabola to never

cross and you could get no soup you

could get no solutions so keep in mind

those are always possibilities when

you're solving a linear quadratic system

and it'll all depend on what you get for

your discriminant when you're using your

quadratic formula or you don't have to

use quadratic formula you could factor

as well if it's factorable but let's see

how it works so basically you're going

to use substitution to solve only a

linear quadratic system so you're going

to make the Y values equal and then

solve for what value of x makes that

happen so I'm just going to substitute

5x plus 9 into the other equation for y

so I'll get 5x plus 9 equals x squared

plus 4x plus 3 and then you'll go ahead

and solve this equation so set it to 0

move everything to the right x squared

plus 4x minus 5x plus 3 minus 9 so I

moved the 5x and the 9 over simplify as

much as you can by collecting like terms

and then solve this equation so you can

use quadratic formula like I said but I

noticed this one is easily factorable

find two numbers with a product of

negative 6 and a sum of negative 1 so

those two numbers are negative 3 & 2

they multiply to negative 6 as negative

1 so it factors to X minus 3 and X plus

2 set each factor to 0

and solved so my first point of

intersection is going to have an x

coordinate of 3 my second point of

intersection is going to have an x

coordinate of negative Q so let's look

at our first point of it so we're going

to get two answers right it's going to

be a secant line our point of

intersection number one if we want the y

coordinate all we have to do is take the

x value of 3 and plug it back into

either of the original equations it

should give us the same answer because

they put their crossing at this point

the linear equation is going to be the

easier evaluation so 5 X plus 9 so I'll

do 5 times 3 plus 9 that gives me 24 my

first point of intersection is the point

324 my second point of intersection I'll

just plug in my second x value negative

2 so y equals 5 times negative 2 plus 9

so negative 10 plus 9 is negative 1 so

my second point of intersection is the

point negative 2 negative 1 what we're

going to do next is rational expressions

how to simplify rational expression so

I'll do this pretty quickly when

dividing two rational expressions the

first thing you're going to want to do

is to change this to a multiplication

question so when dividing fractions what

you have to do is keep the first

fraction the same and then flip the

second fraction so change it to

multiplication flip the second fraction

okay now that it's a multiplication

question what you're going to want to do

is factor as much as possible so the

numerator the first fraction multiplies

to 10 adds negative 7 our negative Q and

negative 5 so that would go to X minus 2

times X minus 5 the denominator is the

difference of squares

it's an x squared minus a 2 squared so

that goes to X minus 2 times X plus 2

this fraction over here common factor

the top divided 3 from both terms we get

3 times X plus 2

denominators multiplies the negative 5

adds to negative 4 or negative 5 and 1

so it goes to X minus 5

X plus one and when we have two

fractions being multiplied we are

allowed to reduce within the same

fraction but we're also allowed to cross

reduce so like these X minus 2's I have

an X minus two divided by an X minus two

within the same fraction you're always

allowed to reduce in the same fraction

as long as your numerator and

denominator are both fully factored so X

minus 2 over X minus 2 is 1 so I can

essentially cross those off but because

we're multiplying we are also allowed to

cross reduce I can reduce this X minus 5

with this X minus 5 to be 1 as well and

then I can cross reduce this X plus 2

it's this X plus 2 and that's all the

reduces and please only reduce when your

numerators and denominators are fully

factored and what I'm left with is just

3 over X plus 1 and you'll have to state

your restrictions and that just means

what values of X would make the

denominator any point be 0

and keep in mind since it was a division

question this whole thing was a

denominator at once so we have to check

the numerator and the denominator of

this one so but right because this x

squared minus 4x minus 5 I'm sorry this

3x plus 6 used to be in the denominator

of this fraction but then what's what we

still have to check it so we check here

X can't be negative 2 X can't be

negative 1 can't be 5 can't be negative

2 you can't be the only one we wouldn't

check it's here that's the only one we

wouldn't have to worry about checking

for division question but check the rest

so X can't be 2 negative 2 5 negative 1

negative 2 and we'll write them in

ascending order so negative 2 negative 1

2 5 so restrictions are what values of X

would make the denominator at any point

be 0 so check this check this and it's

easiest to check when it's all been

factored let's do a subtraction question

with rational expressions

so when subtracting you're going to need

a common denominator but it's probably

going to be easiest to find a common

denominator once we make sure this is

fully factored so this numerator keep -

not a difference of squares it

so we can't use a special product for

this it's not a difference of squares we

just have to leave it there's nothing we

can do it x squared plus 4 but the

denominator multiplies the six adds

negative seven that's negative six and

negative one so we can factor 2x minus 6

X minus 1 minus 8 over X minus 6 we want

a common denominator they both have an X

minus 6 so I just have to multiply this

one top and bottom by X minus 1 and now

they have a common denominator so I can

write them as a single fraction over

that common denominator so I can put the

x squared plus 4 minus 8 times X minus 1

all over our common denominator of X

minus 6 times X minus 1 and then what we

do is we simplify the numerator as much

as possible and then see if there's

anything that can be reduced further so

please make sure you know you can do not

do that you can't cancel these this X

minus 1 in the numerator is not a factor

of everything in the numerator the

numerator is not fully factored so you

cannot reduce anything right now start

by expanding the numerator so x squared

plus 4 distribute the negative 8 so I

get minus 8x plus 8 leave the

denominator alone leave it fully

factored and simplify the numerator

collect your like terms so I have x

squared minus 8x and 4 plus 8 is 12 and

then we would check can the numerator be

factored ringing that multiplies 12 adds

negative 8 yep negative 6 and negative Q

so I can factor it 2x minus 6 times X

minus 2 now the entire numerator and the

entire denominator are factored so now I

can reduce if there's anything that

reduces so what I can do is I can reduce

this X minus 6 over X minus 6 to be

equal to 1 and what we're left with is X

minus 2 over X minus 1 and we just have

to state our restrictions so even though

this X minus 6 has been cancelled out

throughout the process you still have to

take that into consideration

stating your restrictions at any point

throughout the process if X was 6 or 1

our denominator would have gone to 0 and

we would have had an undefined equation

so X can't be 1 it can't be sick so look

at the denominator all the way through

the next section you would have done is