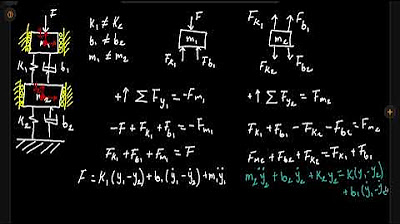Sistema de doble suspension horizontal
Summary
TLDREste video presenta el desarrollo de un modelo matemático para un sistema de suspensión horizontal con dos masas, resortes y amortiguadores. Se analiza la dinámica del sistema bajo la acción de una fuerza externa, considerando la fricción como un amortiguador adicional. Se establecen referenciales y se crean diagramas de cuerpo libre para ambas masas. Se derivan ecuaciones de movimiento basadas en la sumatoria de fuerzas, obteniendo dos ecuaciones diferenciales que modelan el comportamiento del sistema, destacando la interacción entre las masas y los elementos de suspensión.
Takeaways
- 🔍 El vídeo trata sobre la generación de un modelo matemático para un sistema de suspensión horizontal con dos masas, resortes y amortiguadores.
- 🧭 Se menciona que la fuerza externa (denotada como \( F_e \)) es la causante de la dinámica del sistema y se considera unidimensional.
- 🔗 Se observa que hay fricción entre la masa 1 y el suelo, la cual se modela como un componente de amortiguación.
- 📏 Se establecen referenciales bidimensionales para cada masa, aunque el análisis será unidimensional, facilitando la medición de desplazamientos positivos y negativos.
- 📈 Se crean diagramas de cuerpo libre para cada bloque, identificando las fuerzas que actúan sobre cada masa y cómo estas fuerzas afectan la dinámica del sistema.
- ⚖️ Se plantean ecuaciones para el sistema basadas en la sumatoria de fuerzas en el eje horizontal, considerando la masa, la aceleración y las fuerzas de los resortes y amortiguadores.
- 🔗 Se destaca la interconexión entre las masas a través de los resortes y amortiguadores, lo que se refleja en las ecuaciones a través de términos como \( x_1 - x_2 \).
- 📉 Se modela la fricción como una fuerza que actúa contra la dinámica del sistema, similar a cómo se modela el efecto de los amortiguadores.
- 🔄 Se resuelven las ecuaciones para encontrar la relación entre las posiciones y velocidades relativas de las masas, lo que es crucial para entender el comportamiento del sistema.
- 📚 El vídeo educa sobre cómo se generan modelos matemáticos para sistemas físicos complejos y cómo se aplican conceptos de física y matemáticas para resolver problemas reales.
Q & A
¿Qué es el objetivo principal del vídeo?
-El objetivo principal del vídeo es generar el modelo matemático para un sistema de suspensión con dos masas, resortes y amortiguadores, y analizar su dinámica bajo la acción de una fuerza externa.
¿Cuál es la configuración del sistema de suspensión descrito en el vídeo?
-El sistema de suspensión está dispuesto de forma horizontal y consiste en dos masas, dos resortes y dos amortiguadores.
¿Qué fuerza externa se considera en el modelo?
-Se considera una fuerza externa denotada como F_ext, que es la causante de la dinámica del sistema.
¿Cómo se modela la fricción en el sistema?
-La fricción se modela como un componente de amortiguación, anotado como v0, y se considera que actúa entre la masa 1 y el suelo.
¿Cuál es la dirección del análisis dinámico del sistema?
-El análisis dinámico del sistema se considera únicamente sobre la horizontal, es decir, se realiza un análisis unidimensional.
¿Cómo se establecen los referenciales para el análisis de las masas?
-Se establecen referenciales bidimensionales para cada masa, pero dado que el análisis es unidimensional, se centra en el eje horizontal.
¿Qué fuerzas actúan sobre la masa 1 en el diagrama de cuerpo libre?
-Sobre la masa 1 actúan la fuerza externa, la fuerza del resorte 1, la fricción (efeb0), la fuerza del resorte 2 y las fuerzas de los amortiguadores 1 y 2.
¿Cómo se relaciona la deformación del resorte 2 con las masas?
-La deformación del resorte 2 está dada por el desplazamiento relativo entre las masas, es decir, x1 - x2.
¿Qué tipo de fuerzas son las que se oponen a la fuerza externa en la masa 1?
-Las fuerzas que se oponen a la fuerza externa en la masa 1 son la fuerza del resorte 1, la fricción, y las fuerzas de los amortiguadores 1 y 2.
¿Cómo se establece la primera ecuación para el sistema?
-La primera ecuación se establece a partir de la sumatoria de fuerzas sobre el eje horizontal x1, considerando la dirección positiva hacia la derecha y las fuerzas que actúan sobre la masa 1.
¿Qué condiciones de operación se consideran para el modelo matemático?
-Se considera que el desplazamiento o la dinámica del sistema será únicamente sobre la horizontal, lo que implica un análisis unidimensional.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)