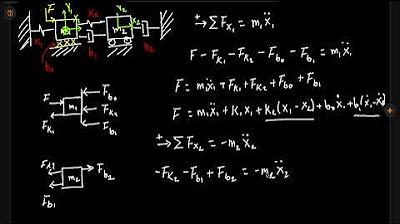Sistema de Suspensión Doble
Summary
TLDREl script de este video se enfoca en el modelado del sistema de doble suspensión Bateman, que tiene como objetivo analizar las interacciones entre dos subsistemas con características similares. Se describe cómo el sistema, compuesto por masas m1 y m2, resortes y amortiguadores, es influenciado por una fuerza externa vertical. A través de la consideración de restricciones y la suposición de un único grado de libertad vertical, se establece un marco de referencia centrado en el centro de masas de los cuerpos. Las ecuaciones de Newton se aplican para establecer las fuerzas y aceleraciones en cada cuerpo, resultando en dos ecuaciones diferenciales interconectadas que describen el sistema. Se discute la relación entre las fuerzas del resorte y del amortiguador con las deformaciones y velocidades relativas, y se plantean soluciones particulares para el caso en que todos los elementos del sistema son iguales. El análisis finaliza destacando la interconexión de las ecuaciones y la imposibilidad de desacoplar el sistema, ofreciendo una visión general del modelado matemático del sistema Bateman.
Takeaways
- 🔍 El video trata sobre el modelado de un sistema de doble suspensión Bateman, que se utiliza para observar las interacciones entre dos subsistemas con características similares.
- 🔧 El sistema está compuesto de dos masas (m1 y m2), dos resortes (resorte 1 y resorte 2) y dos amortiguadores (amortiguador 1 y amortiguador 2), y está excitado por una fuerza externa vertical.
- 🚫 Se asume que el sistema tiene un grado de libertad vertical y que las guías de las masas son sin fricción, lo que permite solo el desplazamiento vertical.
- 📐 Se establecen referenciales en el centro de masa de los cuerpos 1 y 2, con dirección positiva hacia arriba para el análisis unidimensional.
- ⚖️ Se consideran las fuerzas externas, de resorte y amortiguamiento, así como la reacción de las masas contra el desplazamiento, en los diagramas de cuerpo libre.
- 📉 Las ecuaciones de Newton se aplican para modelar las interacciones, resultando en dos ecuaciones diferenciales que describen el sistema.
- 🔗 Las fuerzas del resorte y del amortiguador están relacionadas con las deformaciones y velocidades relativas entre los cuerpos, siguiendo la ley de Hooke y la ecuación de la fuerza del amortiguador.
- 🔄 Las ecuaciones diferenciales resultantes son interconectadas, lo que indica que no es posible resolver una sin considerar la otra, reflejando la interacción entre las masas.
- 📉 Se plantea una solución particular del caso en el que todos los elementos del sistema son iguales, lo que simplifica las ecuaciones y permite analizar el comportamiento del sistema.
- 🔧 La solución generalizada abarca el caso en el que los elementos no son iguales, lo que es necesario para modelar sistemas reales con especificaciones diferentes.
- 🙏 El video concluye agradeciendo la atención y deseando un buen día, invitando a la audiencia a seguir aprendiendo.
Q & A
¿Qué es el modelado de Bateman y qué propósito tiene?
-El modelado de Bateman es un sistema de doble suspensión que se utiliza para observar las interacciones entre dos subsistemas que poseen características similares. Su propósito es analizar cómo estos subsistemas interactúan entre sí bajo la influencia de una fuerza externa.
¿Cómo se considera que el sistema de doble suspensión está excitado?
-El sistema de doble suspensión está excitado por una fuerza externa que se aplica en sentido vertical, como se muestra en el diagrama del video.
¿Cuál es el grado de libertad que se considera para el sistema de doble suspensión?
-Se considera que el sistema tiene únicamente un grado de libertad, que está dado en el sentido vertical, debido a la instalación de restricciones que permiten solo el desplazamiento vertical sin fricción.
¿Cómo se establecen los referenciales en el centro de las masas para el análisis?
-Los referenciales están asignados exactamente en el centro de la masa de los cuerpos 1 y 2, con la dirección considerada positiva hacia arriba.
¿Qué fuerzas actúan sobre la masa 1 y cómo son estas fuerzas?
-La masa 1 se ve afectada por la fuerza externa, la interacción opuesta del resorte 1 y del amortiguador 1. La fuerza de la masa 1 se opone a su estado de reposo y tiende a mantener su posición actual.
¿Cómo se relacionan las fuerzas del resorte y del amortiguador con la masa 2?
-La masa 2 experimenta interacciones regidas por el resorte 1 y el amortiguador 2. La fuerza de la masa 2 y las fuerzas del resorte 2 y del amortiguador 2 están interconectadas y afectan la dinámica del sistema.
¿Cómo se aplican las ecuaciones de Newton en el análisis del sistema?
-Las ecuaciones de Newton se aplican para establecer las fuerzas ejercidas en los cuerpos y para generar las ecuaciones del modelo. Se consideran las fuerzas en una dirección específica y se utilizan para describir la aceleración y la oposición de las masas al desplazamiento.
¿Cómo se relaciona la fuerza del resorte 1 con la deformación que experimenta?
-La fuerza del resorte 1 está directamente proporcional a la deformación que experimenta, que se mide como la diferencia de las posiciones relativas de los dos referenciales.
¿Por qué no se pueden desacoplar las ecuaciones del sistema de doble suspensión?
-No se pueden desacoplar las ecuaciones porque las fuerzas del resorte y del amortiguador de una masa afectan a la otra, y aparecen términos en las ecuaciones que hacen alusión a estos elementos interconectados.
¿Qué sucede si todos los elementos del sistema de doble suspensión son iguales?
-Si todos los elementos son iguales, se puede establecer una relación donde las masas m1 y m2 son iguales, y las constantes de amortiguamiento b1 y b2, así como las fuerzas f1 y f2, son también iguales. Esto permite plantear una solución particular para el caso.
¿Cómo se resuelven las ecuaciones diferenciales del sistema si no son desacopladas?
-Las ecuaciones diferenciales no desacopladas se resuelven simultáneamente, teniendo en cuenta que una ecuación afecta a la otra. Esto significa que no se puede encontrar una solución para una ecuación sin considerar la otra.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)