Sumatorias

Rodrigo Lugo

16 Sept 202005:52

Summary

TLDREn este curso de cálculo integral, se explora la importancia de las sumatorias en el cálculo integral. Se explica que el cálculo integral se basa en determinar el área bajo una curva, lo que implica sumar áreas en un intervalo específico. La sumatoria, representada con el símbolo 'sigma', es una herramienta clave para simplificar la suma de términos en series numéricas. Se presentan ejemplos prácticos, como sumar números desde el 4 al 15, o calcular los cuadrados de los números desde el 2 al 6. Estas sumatorias son esenciales para entender cómo se calcula el área en el cálculo integral, conectando el concepto de sumar rectángulos debajo de una curva. Se promete una explicación detallada de las propiedades de las sumatorias en un próximo video.

Takeaways

🔢 Las sumatorias son fundamentales en el cálculo integral porque permiten calcular áreas debajo de curvas al sumar infinitesimales rectángulos.
📏 La notación sigma (Σ) representa la operación de sumatoria, indicando la suma de un conjunto de términos.
📐 Se utiliza la sumatoria para simplificar la representación de la suma de una secuencia de números, como de 1 a n.
📈 La sumatoria se puede aplicar a funciones, como la suma de los cuadrados de los números desde 2 hasta 6.
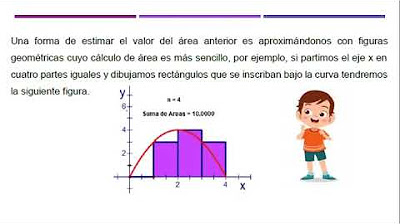
📘 El cálculo integral geométrico se basa en la idea de sumatoria, donde se suman áreas de rectángulos para aproximar el área bajo una curva.
📙 En el cálculo integral, la sumatoria de áreas de rectángulos se utiliza para aproximar el área bajo una función continua.
📖 Se presentan ejemplos prácticos para ilustrar cómo se aplican las sumatorias, facilitando la comprensión de la técnica.
📊 La sumatoria es una herramienta matemática poderosa que se utiliza para abordar problemas de cálculo integral y series.
📚 Se menciona que se explorarán las propiedades de las sumatorias en un vídeo futuro, lo que sugiere una profundización en el tema.
📝 La simplicidad de la notación de sumatoria contrasta con la complejidad de los problemas que resuelve, resaltando su utilidad en matemáticas.

Q & A

¿Qué es la sumatoria y cómo se relaciona con el cálculo integral?
-La sumatoria es una operación matemática que se utiliza para sumar un conjunto de términos, generalmente denotada por el símbolo 'Σ'. Se relaciona con el cálculo integral porque el problema original del cálculo integral es determinar el área bajo una curva, lo cual se puede entender como una suma de áreas de rectángulos infinitesimales debajo de la curva.
¿Cómo se representa la notación de sumatoria en matemáticas?
-La notación de sumatoria se representa con el símbolo 'Σ', donde se indica el índice de inicio y el límite superior de la suma. Por ejemplo, Σ(i=1 a n) a_i significa sumar todos los términos a_i desde i=1 hasta i=n.
¿Qué es el significado de 'i' en una sumatoria?
-En una sumatoria, 'i' es un índice de sumación que varía desde un valor inicial hasta un valor final. Por ejemplo, en la sumatoria de los cuadrados de los números desde 2 hasta 6, 'i' toma los valores de 2, 3, 4, 5 y 6.
¿Cómo se calcula la suma de los números del 4 al 15?
-Para calcular la suma de los números del 4 al 15, se suman todos los números enteros desde el 4 hasta el 15, lo cual se puede representar como Σ(i=4 a 15) i.
¿Qué es la suma de los cuadrados de los números desde el 2 hasta el 6?
-La suma de los cuadrados de los números desde el 2 hasta el 6 se calcula sumando el cuadrado de cada número en ese rango, es decir, 2^2 + 3^2 + 4^2 + 5^2 + 6^2.
¿Cómo se abrevia la suma de múltiplos de 5 desde 3 hasta 5?
-La suma de múltiplos de 5 desde 3 hasta 5 se abrevia como Σ(i=3 a 5) 5i, lo que significa sumar 5*3, 5*4 y 5*5.
¿Cuál es la diferencia entre una sumatoria y una simple suma de números?
-Una sumatoria es una notación matemática que abrevía la suma de un conjunto de términos, permitiendo expresar la operación de suma de una manera más compacta y eficiente, especialmente cuando se trabaja con series de números o expresiones algebraicas.
¿Por qué son importantes las sumatorias en el cálculo integral?
-Las sumatorias son importantes en el cálculo integral porque proporcionan una herramienta para modelar la integración geométrica como una suma de áreas de rectángulos o trapecios debajo de una curva, lo que es fundamental para calcular áreas y volúmenes en el análisis matemático.
¿Qué se entiende por 'propiedades de las sumatorias'?
-Las propiedades de las sumatorias son reglas y relaciones que permiten manipular y simplificar expresiones de sumatorias. Estas propiedades son útiles para realizar cálculos más eficientes y para entender mejor cómo se comportan las sumas en contextos más complejos.
¿Cómo se puede aprender a manejar mejor las sumatorias y sus propiedades?
-Para aprender a manejar mejor las sumatorias y sus propiedades, es útil practicar con ejemplos específicos, estudiar las reglas de manipulación de sumatorias y aplicarlas en problemas de cálculo integral y series matemáticas.

Outlines

00:00

📘 Introducción a las Sumatorias en Cálculo Integral

Este párrafo introduce el tema de las sumatorias en el contexto del cálculo integral. Se explica que las sumatorias son esenciales para entender cómo se calcula el área bajo una curva, que es el problema central del cálculo integral. Se menciona que la integral es una suma de áreas infinitesimales y se utiliza el símbolo de sumatoria (sigma) para representar la suma de términos. Se da un ejemplo práctico de cómo se representa la suma de números desde el 4 hasta el 15, y se explica cómo se abrevía utilizando la notación de sumatoria. Además, se presentan otros ejemplos para ilustrar cómo se suman los cuadrados de los números desde el 2 hasta el 6 y la multiplicación de 5 por un índice variable desde 3 hasta 5. El párrafo finaliza con una mención de que se explorarán las propiedades de las sumatorias en un video futuro.

05:02

📐 Sumatorias y Cálculo Integral Geométrico

En este segundo párrafo, se profundiza en la relación entre las sumatorias y el cálculo integral geométrico. Se describe cómo, al realizar una integral geométrica, se está efectivamente realizando una suma de áreas de rectángulos que se encuentran debajo de una curva. Esto se relaciona con la idea de sumar infinitesimales para calcular el área total. El vídeo previo mencionado abordó la introducción al cálculo integral, y este párrafo establece la conexión entre las sumatorias y el cálculo integral. Se promete que en un video subsiguiente se explorarán las propiedades de las sumatorias de manera detallada y se hará hincapié en su simplicidad a pesar de la complejidad aparente de los símbolos involucrados.

Mindmap

Keywords

💡Cálculo Integral

El cálculo integral es una rama del cálculo matemático que se enfoca en el estudio de la integración, es decir, el proceso de encontrar una función a partir de su derivada o el área bajo una curva. En el guion del video, se menciona que el cálculo integral tiene que ver con determinar el área debajo de una curva, lo cual es fundamental para entender la necesidad de las sumatorias en este contexto.

💡Sumatorias

Las sumatorias son una herramienta matemática utilizada para simplificar la adición de múltiples términos en una secuencia. En el video, se explica que las sumatorias son necesarias para el cálculo integral, ya que permiten sumar áreas discretas debajo de una curva, lo cual es esencial para calcular áreas en el cálculo integral.

💡Área debajo de una curva

Este concepto se refiere a la medida del espacio que se encuentra debajo de una función y por encima del eje x en un intervalo dado. En el guion, se destaca que el cálculo integral busca determinar esta área, y es aquí donde las sumatorias intervienen para sumar las áreas de pequeños rectángulos que se acumulan debajo de la curva.

💡Sigma (Σ)

El símbolo de la suma, representado por Σ, es el que se utiliza para indicar una sumatoria en matemáticas. En el video, se describe cómo este símbolo abrevia la notación al sumar una serie de términos, como se ve en ejemplos donde se suman números desde el 4 hasta el 15, o los cuadrados de números desde el 2 hasta el 6.

💡Rectángulos

En el contexto del cálculo integral, los rectángulos son figuras geométricas que se utilizan para aproximar la área bajo una curva. En el guion, se menciona que al realizar una integral geométricamente, se está realizando una sumatoria de áreas de rectángulos, lo que ilustra cómo se aproxima el cálculo de áreas mediante sumatorias.

💡Propiedades de las sumatorias

Aunque no se detallan en el guion proporcionado, las propiedades de las sumatorias son reglas matemáticas que gobiernan cómo se pueden manipular y calcular las sumas. Se menciona que se explorarán en un próximo video, lo que implica que son un aspecto importante de cómo se aplican las sumatorias en el cálculo integral.

💡Valores límite inferior y superior

Estos valores definen el rango dentro del cual se realiza la sumatoria. En el guion, se ejemplifica cómo se utilizan estos valores para determinar desde qué número comienza y hasta qué número se llega en la sumatoria, como en el caso de sumar desde el 4 hasta el 15, o los cuadrados de números desde el 2 hasta el 6.

💡Cuadrados de un número

En el video, se utiliza el ejemplo de sumar los cuadrados de los números desde el 2 hasta el 6 para ilustrar cómo se aplican las sumatorias. Esto demuestra cómo se pueden aplicar operaciones matemáticas dentro de una sumatoria, sumando no solo los números, sino sus cuadrados.

💡Multiplicación dentro de sumatorias

Se menciona en el guion un ejemplo donde se multiplica un número 'i' por 5 en una sumatoria que varía desde 3 hasta 5. Esto muestra cómo se pueden incluir operaciones de multiplicación dentro de las sumatorias, lo que es común en el cálculo integral para calcular áreas más complejas.

💡Anotación

La anotación en matemáticas se refiere a la forma en que se escriben las fórmulas y operaciones. En el guion, se discute cómo las sumatorias simplifican la anotación al reemplazar listas de términos por una notación más compacta, como se ve en el símbolo sigma (Σ), que representa la suma de una serie de términos.

Highlights

Introducción al tema de las sumatorias en el contexto del cálculo integral.

Importancia de las sumatorias en la determinación del área bajo una curva.

Explicación de que el cálculo integral originalmente buscaba medir áreas.

La sumatoria como una herramienta para acumular áreas en intervalos específicos.

Definición de la notación de sumatoria y su simbolismo (sigma).

Ejemplo práctico de sumatoria para sumar números desde 4 hasta 15.

Descripción de cómo se representa la sumatoria de una serie de números.

Ejemplo de sumatoria para calcular los cuadrados de números desde 2 hasta 6.

Método para escribir la sumatoria de potencias de un número variable.

Ejemplo de sumatoria para multiplicar un número por un índice variable desde 3 hasta 5.

Importancia de la notación de sumatoria en el cálculo integral para simplificar cálculos.

Promesa de explorar las propiedades de las sumatorias en un próximo video.

Comparación de la notación de sumatoria con la anotación extensa de números.

Enfatización de la simplicidad y utilidad de la notación de sumatoria en cálculo.

Anuncio de la continuación del tema en futuras lecciones.

Invitación a los estudiantes a familiarizarse con los símbolos de sumatoria.