Integral de una constante
Summary
TLDREn este video, el profesor aborda la integral de funciones constantes, una de las operaciones más sencillas en cálculo integral. Se destaca la importancia de entender no solo cómo realizar la integración, sino también las razones detrás de cada paso. Se discuten las propiedades fundamentales de las integrales, como la integral del diferencial de X (x + c) y cómo manejar constantes al integrar. A lo largo del video, se resuelven ejemplos prácticos para ilustrar los conceptos y se motiva a los estudiantes a practicar y comparar sus soluciones con las proporcionadas. Además, se enfatiza la utilidad de la integración en el cálculo de áreas y su relación con el teorema fundamental del cálculo, que conecta la derivada y la integral. Finalmente, el profesor alienta a los estudiantes a seguir explorando el tema a través de otros videos del curso y a compartir y comentar el contenido para fomentar el aprendizaje en comunidad.
Takeaways
- 📚 La integral de una constante es la constante misma más la constante de integración.
- 🔢 La integral del diferencial de una variable (por ejemplo, d/dx X) es la variable más una constante de integración (X + C).
- ⚖️ Cuando una constante está acompañada del diferencial de una variable, la constante puede ser extraída de la integral.
- 📈 La derivada de una variable a la primera (d/dx X) es 1, y por el Teorema Fundamental del Cálculo, la integral de 1 es X.
- 🛠️ La integración es el proceso opuesto a la derivación, y se utiliza para encontrar áreas bajo curvas y resolver problemas relacionados con el cálculo.
- 📌 Es importante recordar que en matemáticas, las letras generalmente representan variables, pero en ciertos contextos pueden tratarse como constantes.
- 📉 La integral de una función es la antiderivada de esa función, y se utiliza para encontrar la suma de los valores de la función en un intervalo.
- 📌 Al integrar, se debe tener cuidado con las propiedades algebraicas, como el manejo de constantes dentro de las expresiones.
- 🔁 La práctica de integrar y derivar funciones ayuda a comprender mejor los conceptos y para verificar la corrección de las soluciones.
- 📝 Al resolver ejercicios de integración, se pueden saltar algunos pasos si se tiene claro el proceso, pero siempre es recomendable escribir la constante de integración.
- 📐 La integración de funciones es una herramienta poderosa en matemáticas, física y otras disciplinas, y es fundamental para el análisis de funciones y la comprensión de conceptos avanzados.
Q & A
¿Cómo se encuentra la integral de una constante?
-Para encontrar la integral de una constante, se deja la constante fuera del integral, se agrega la variable que en este caso es 'x', y se le suma la constante de integración.
¿Por qué siempre se debe agregar la constante de integración en la integral?
-Se agrega la constante de integración porque la integral es una antiderivada y puede haber múltiples funciones que tomen el mismo valor para un cierto intervalo, por lo que la constante de integración representa las soluciones posibles adicionales.
¿Cuál es la primera propiedad de las integrales mencionada en el script?
-La primera propiedad mencionada es que la integral del diferencial de 'x' es 'x' más una constante (x + c).
¿Cómo se justifica que la integral de una constante sea la constante misma multiplicada por la variable de integración?
-Se justifica a través de la derivada, ya que la derivada de una constante multiplicada por una variable es la constante, y dado que la integral es la operación opuesta a la derivada, la integral de una constante es la constante misma multiplicada por la variable de integración.
¿Cómo se puede verificar si una integral se ha resuelto correctamente?
-Se puede verificar derivando la respuesta obtenida. Si la derivada de la integral es la función original, entonces se ha resuelto correctamente.
¿Qué es lo que se debe recordar cuando se tiene un número acompañado de una 'x' en una integral?
-Se debe recordar que el número es una constante y se puede sacar de la integral, dejando el diferencial de 'x', el cual se integra como 'x' más una constante de integración.
¿Por qué es importante entender el concepto detrás de la integración y no solo cómo hacerlo?
-Es importante entender el concepto detrás de la integración para poder aplicarlo adecuadamente en diferentes situaciones y para comprender las propiedades y justificaciones matemáticas que lo respaldan.
¿Cómo se maneja una integral cuando la variable es una letra diferente a 'x', como en el caso de 'u'?
-Cuando la variable es una letra diferente a 'x', como 'u', se realiza la integral como se haría con 'x', pero se tiene en cuenta que la variable de integración es 'u', por lo que la constante de integración se escribe con 'u' en lugar de 'x'.
¿Cómo se resuelve una integral que contiene una constante multiplicando a la integral de otra expresión?
-Se saca la constante fuera de la integral y se realiza la integral de la expresión restante. Luego, se multiplica el resultado por la constante y se agrega la constante de integración.
¿Qué hace si una constante está en el denominador de una fracción en una integral?
-Si una constante está en el denominador, se saca la constante tanto del numerador como del denominador, y se realiza la integral de la fracción resultante.
¿Cómo se identifica si una letra en una integral es una constante o una variable?
-Se identifica como una constante si la letra representa un número que no cambia, y como una variable si la letra representa una función o una entidad que varía. En el contexto de una integral, si la letra no está acompañada de un diferencial, generalmente se considera una constante.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Integrales | Por qué se pone +c

Introducción al concepto de antiderivada 1 (integral indefinida)

¿Qué son las antiderivadas? ¿Cómo funcionan? | EasyMaths Colombia

2. Integrales. Integrales indefinidas.

Curso de Integrales. Capítulo 1: ¿Qué es y para qué sirve la integral? Una propuesta didáctica.
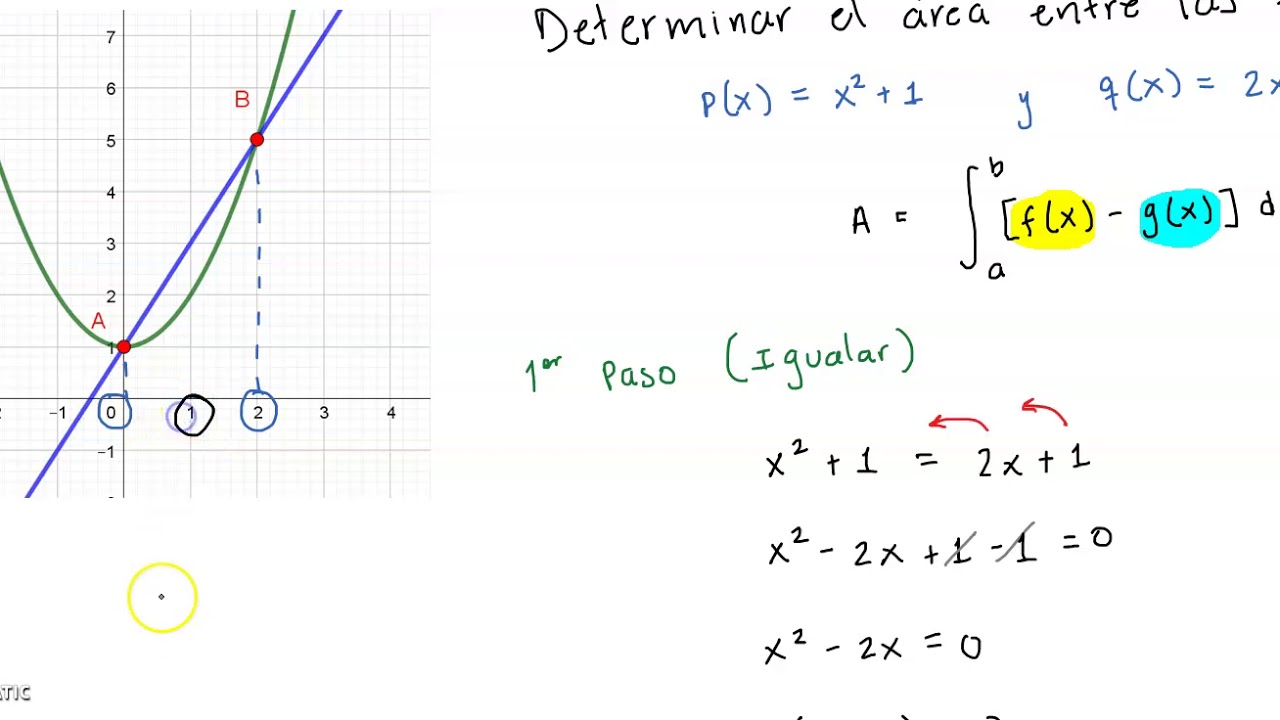
AREA ENTRE CURVAS EJEM1
5.0 / 5 (0 votes)
