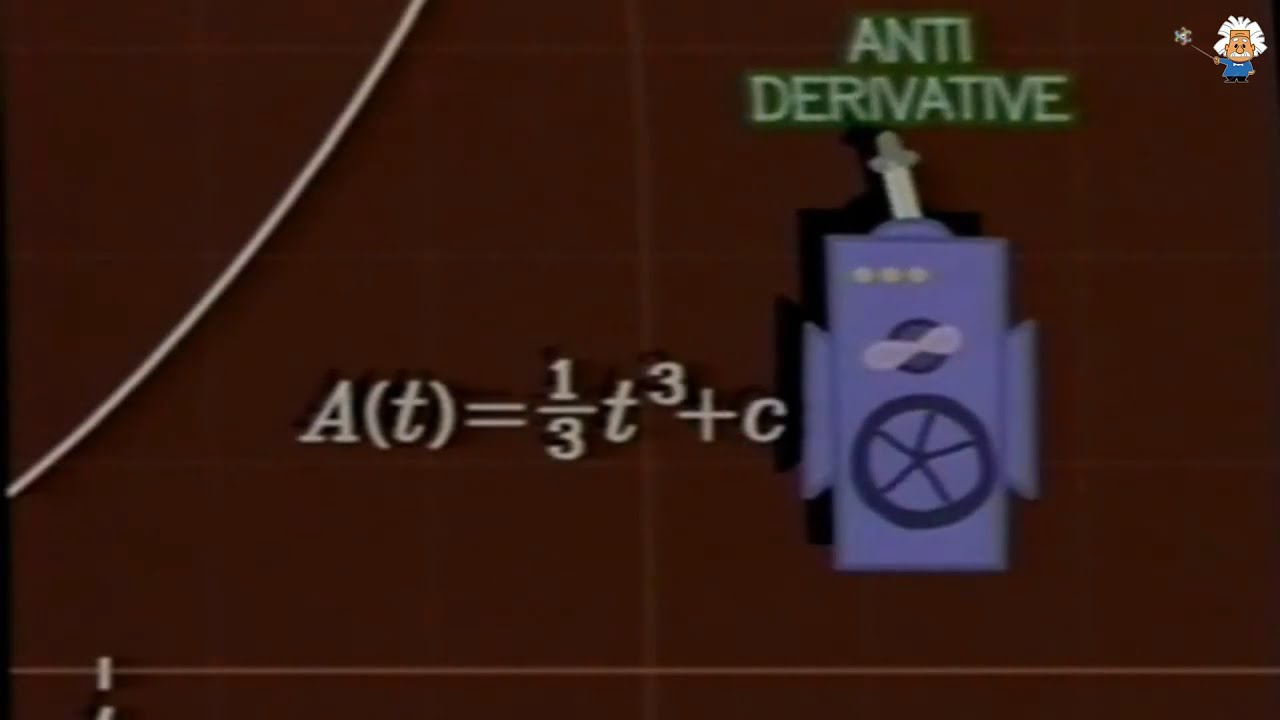The Birth Of Calculus (1986)
Summary
TLDRThis script explores the invention of calculus by Isaac Newton and Gottfried Wilhelm Leibniz, highlighting their independent discoveries and the evolution of their mathematical methods. It delves into Newton's early work on tangents and areas, his development of a universal method for finding tangents, and Leibniz's geometric approach to areas and his introduction of integral and differential calculus symbols. The narrative underscores the significance of their work in advancing mathematical power and the automation of reasoning processes.
Takeaways
- 📚 Calculus is a fundamental tool in modern mathematics, with key contributions from Isaac Newton and Gottfried Wilhelm Leibniz.
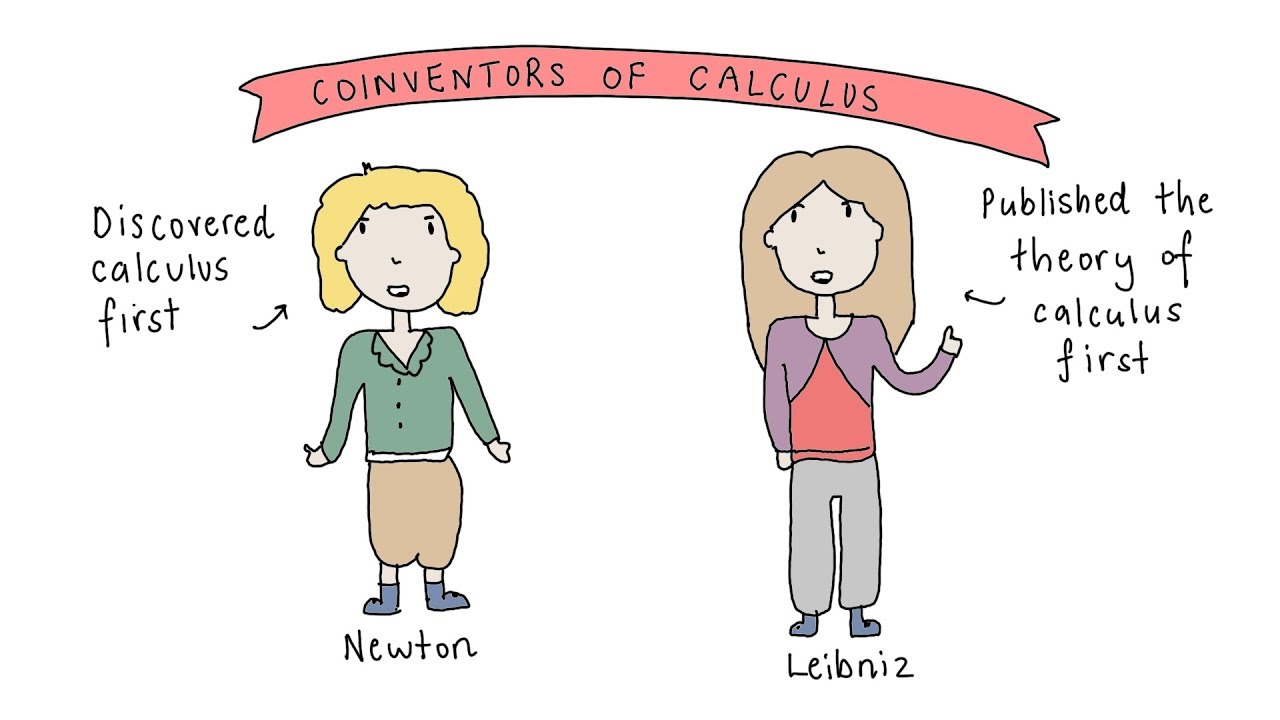
- 🕰️ Newton first discovered calculus around 1665-1666, while Leibniz made his independent discovery about 10 years later.
- 📖 Both Newton and Leibniz's original writings on their discoveries are preserved, providing insight into their mathematical processes.
- 🎓 Newton's early work in calculus was influenced by his studies at Trinity College, Cambridge, and his intense work period from 1665.
- 📐 Newton's initial approach to calculus involved improving methods for finding tangents to polynomial curves, using circles and the method of normals.
- 🔍 Newton realized the inverse relationship between tangent problems and area problems, leading to his development of methods for calculating areas under curves.
- 🛣️ Newton's work extended to 'mechanical curves,' such as the cycloid, which are defined by motion rather than polynomial equations.
- 🔄 Newton's key insight was the ratio of velocities of two points moving along the x and y axes, leading to a new method for finding tangents to any curve.
- 📈 Leibniz's calculus was influenced by the study of area and tangency problems, and his approach was more geometric, using infinite sums of ordinates.
- 📝 Leibniz introduced the integral sign (∫) and the differential symbol (d), laying the foundation for differentiation and integration in calculus.
- 🔧 Both Newton and Leibniz aimed to automate and formalize mathematical reasoning, with Leibniz focusing on creating a universal algorithm for his calculus.
Q & A
Who are the two men credited with inventing calculus?
-Isaac Newton and Gottfried Wilhelm Leibniz are the two men credited with inventing calculus.
When did Newton first discover his calculus?
-Newton first discovered his calculus in 1665 or 1666.
What was the method used by Newton to find the tangent to a polynomial curve?
-Newton used the method of finding a circle with a center on the x-axis that just touches the curve at point P, where the line from the center of the circle to P is called a normal, and the line at right angles to this normal through P is the tangent.
What was the significance of Newton's work with mechanical curves?
-Newton's work with mechanical curves, such as the cycloid, led him to a new way of looking at all curves by perceiving them as generated by movement, which was a fundamental perception of the problem and led to a new method for finding tangents.
What was the key insight that led Newton to a new method for finding tangents?
-Newton's key insight was the concept of the ratio of the velocities of two points moving along the curve, which he used to determine the direction of the tangent.
What was the significance of Leibniz's introduction of the integral sign?
-The introduction of the integral sign by Leibniz was significant as it marked the first occurrence of a symbol that remains unchanged to the present day, symbolizing the sum of all the ordinates in his method for finding areas.
What was Leibniz's approach to finding areas under curves?
-Leibniz's approach to finding areas under curves involved considering the area as made up of all the ordinates taken infinitely close together, which gave the area directly.
How did Leibniz's calculus differ from Newton's in terms of notation and conceptualization?
-Leibniz's calculus used differentials and infinite linear points of curves, focusing on a bold geometrical analogy, while Newton's calculus was more focused on the idea of motion and change in time, using the language of fluxions.
What was the impact of the calculus as described by Newton and Leibniz on the field of mathematics?
-The calculus as described by Newton and Leibniz had a profound impact on mathematics, arguably providing the greatest increase in its power since the time of the Greeks.
What was the motivation behind Leibniz's development of his calculus?
-Leibniz's motivation behind the development of his calculus grew out of his study of contemporary mathematical problems, particularly area and tangency problems, and his desire to systematize mathematical reasoning.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)