El asombroso Teorema de Pitágoras
Summary
TLDREste video ofrece una introducción al Teorema de Pitágoras, una herramienta matemática fundamental para calcular la hipotenusa en triángulos rectángulos. Explica la vida y obra de Pitágoras, su influencia en la música y la astronomía, y cómo su teorema se aplica en contextos modernos como la construcción y la navegación. Además, presenta un desafío práctico para calcular la longitud de una pared usando un escuadra, y menciona el curso de preparación para el TOEFL en Platzi, destacando su relevancia para estudios y migración internacional.
Takeaways
- 📚 El TOEFL es un examen solicitado para estudiar o trabajar en el extranjero, y Platzi ofrece un descuento para prepararse.
- 🧮 El Teorema de Pitágoras se utiliza para calcular la longitud de la hipotenusa de un triángulo rectángulo si se conocen las longitudes de los catetos.
- 🏗️ El Teorema de Pitágoras fue descubierto por Pitágoras de Samos, un filósofo griego que vivió hace más de 2,500 años, y es fundamental en la matemática.
- 🎵 Los pitagóricos, seguidores de Pitágoras, creían que todo en el universo se podía describir mediante relaciones geométricas y numéricas, y que los números eran la esencia de las cosas terrenales.
- 🎵 También desarrollaron una teoría matemática de la música basada en la relación entre las longitudes de las cuerdas y las notas que producen.
- 🌐 El Teorema de Pitágoras se aplica a triángulos rectángulos, independientemente del tamaño de sus lados o su orientación.
- 📐 El hipoténusa es el lado opuesto al ángulo recto y es el más largo, mientras que los otros dos lados se llaman catetos.
- 🔢 La relación matemática del Teorema de Pitágoras se expresa como a² + b² = c², donde a y b son los catetos y c es el hipoténusa.
- 🕷️ Se ilustra el uso práctico del Teorema de Pitágoras con un ejemplo de Spiderman, que necesita calcular la longitud de su red para salvar un bebé.
- 🏡 El Teorema de Pitágoras se aplica en la construcción y la arquitectura, como en el cálculo de la longitud de techos inclinados en la construcción de casas.
- 🌟 El Teorema de Pitágoras ha sido probado y demostrado por diversas culturas a lo largo de la historia, y es uno de los teoremas con más pruebas diferentes.
Q & A
¿Qué es el TOEFL y por qué es importante mencionarlo en el guion?
-El TOEFL es un examen de competencia en inglés que es requerido para estudiar o trabajar en el extranjero. Es importante mencionarlo porque el video ofrece un descuento para prepararse para este examen a través de Platzi.
¿Cómo se relaciona el Teorema de Pitágoras con la medición de una pared que es difícil de escalar?
-El Teorema de Pitágoras se relaciona con la medición de una pared porque permite calcular la longitud de la hipotenusa (el lado opuesto al ángulo recto) si se conocen los otros dos lados de un triángulo rectángulo, lo que es útil cuando no se puede medir directamente la altura de una pared.
¿Quién fue Pitágoras de Samos y qué aportó a la matemática?
-Pitágoras de Samos fue un filósofo griego conocido como el 'primer matemático puro'. Fundó una sociedad matemática y musical conocida como 'los pitagóricos', y aportó el Teorema de Pitágoras, que describe la relación entre los lados de un triángulo rectángulo.
¿Cuál es la definición de un triángulo rectángulo según el guion?
-Un triángulo rectángulo es cualquier triángulo que tiene un ángulo recto, es decir, de 90 grados.
¿Qué es la hipotenusa en un triángulo rectángulo y cómo se relaciona con el Teorema de Pitágoras?
-La hipotenusa es el lado opuesto al ángulo recto en un triángulo rectángulo y es el lado más largo. Según el Teorema de Pitágoras, la suma de los cuadrados de los otros dos lados (las piernas) es igual al cuadrado de la hipotenusa.
¿Cómo se demuestra algebraicamente el Teorema de Pitágoras utilizando el ejemplo del lazo del Spiderman?
-En el ejemplo, se conocen dos lados del triángulo (7 metros y 24 metros) y se busca la hipotenusa. Se aplica el Teorema de Pitágoras (a^2 + b^2 = c^2), donde 7^2 + 24^2 = c^2, resultando en 625, y luego se toma la raíz cuadrada para encontrar que c es 25 metros.
¿Cómo se utiliza el Teorema de Pitágoras para calcular la altura de una pared cuando se conoce la longitud de la escalera y la distancia desde el muro?
-Se aplica el Teorema de Pitágoras donde la escalera representa la hipotenusa y la distancia desde el muro representa una de las piernas. Se resuelve la ecuación para encontrar la longitud de la otra pierna, que en este caso es la altura de la pared.
¿Cuál es la importancia de los triples pitagóricos y cómo se relacionan con el Teorema de Pitágoras?
-Los triples pitagóricos son conjuntos de tres números enteros que satisfacen el Teorema de Pitágoras (a^2 + b^2 = c^2). Son importantes porque proporcionan ejemplos prácticos de la aplicación del teorema en triángulos rectángulos con lados enteros.
¿En qué áreas se aplica el Teorema de Pitágoras en la vida real?
-El Teorema de Pitágoras se aplica en construcción, arquitectura, ingeniería civil, navegación marítima y aérea, y en la creación de modelos 3D para videojuegos y películas.
¿Cuál es la relevancia de los diferentes tipos de pruebas del Teorema de Pitágoras mencionadas en el guion?
-La relevancia de las diferentes pruebas del Teorema de Pitágoras es demostrar su validez y universalidad. A lo largo de la historia, diversas culturas y matemáticos han desarrollado pruebas diferentes, lo que demuestra la importancia y el impacto duradero del teorema en la matemática.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Teorema de Pitágoras | Ejercicio de práctica

Teorema de Pitágoras - MasterD
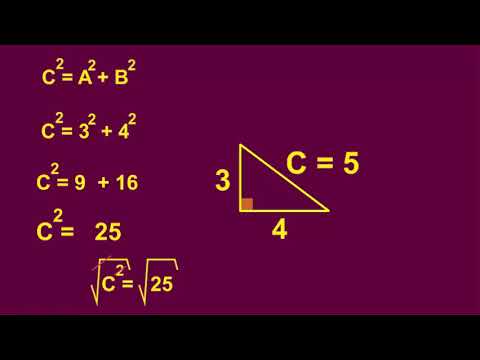
TEOREMA DE PITÁGORAS y su verificación gráfica, en solo dos minutos

Razones TRIGONOMÉTRICAS 📐

¿Qué es el Teorema de Pitágoras? | Videos Educativos Aula365

Matemática 1 TRIGONOMETRÍA 2da parte funciones trigonométricas en triángulos cualquiera
5.0 / 5 (0 votes)
