MÉTODO DE ARQUÍMEDES PARA CALCULAR EL ÁREA DE UNA CIRCUNFERENCIA
Summary
TLDREn este video, se explora el estudio de la integral definida y las sumas de Riemann, iniciando con los antecedentes históricos de Arquímedes, quien en el siglo 3 a.C. calculó áreas y superficies, contribuyendo significativamente al concepto de pi y el área de una circunferencia. Se ilustra el método de Arquímedes para calcular el área de una circunferencia utilizando rectángulos inscritos y circunscritos, comparándolo con la fórmula actual de pi multiplicado por el radio al cuadrado. El resultado del método empírico de Arquímedes se aproxima notablemente al valor obtenido por la fórmula matemática.
Takeaways
- 📚 La clase trata sobre el estudio de la integral definida y las sumas de Riemann.
- 👨🔬 Arquímedes, en el siglo 3 a.C., fue el primero en calcular áreas y superficies, contribuyendo significativamente a la física y las matemáticas.
- 🔍 Arquímedes introdujo el concepto de pi y el cálculo del área de una circunferencia, lo cual fue fundamental para futuras investigaciones.
- 🌐 Newton, Leibniz, Barrow y Riemann son matemáticos posteriores que continuaron el trabajo iniciado por Arquímedes.
- 📐 El problema inicial de Arquímedes era calcular el área de figuras geométricas, comenzando con la circunferencia.
- 📏 Se trazaron dos circunferencias con el mismo radio de 5 centímetros para ilustrar el método de Arquímedes.
- 🔶 Se utilizaron rectángulos inscritos y circunscritos para estimar el área de las circunferencias.
- 📏 Los rectángulos tienen una base de 1 centímetro y alturas variables, dependiendo de su posición en relación con la circunferencia.
- 📊 Se calculó el área de cada rectángulo inscrito y circunscrito, sumando un total de 69 cm² para los inscritos y 83,6 cm² para los circunscritos.
- 🧮 El método de Arquímedes propone calcular el área de la circunferencia como la suma de las áreas de los rectángulos inscritos y circunscritos dividida entre 2, obteniendo así aproximadamente 76,3 cm².
- 📌 Se comparó el resultado del método de Arquímedes con la fórmula exacta de pi (pi × radio²), obteniendo un área de 78,54 cm², lo que muestra la proximidad del método empírico a la solución exacta.
Q & A
¿Quién fue la primera persona en calcular áreas o superficies matemáticamente?
-La primera persona en calcular áreas o superficies matemáticamente fue Arquímedes en el siglo 3 antes de nuestra era.
¿Qué aportó Arquímedes a las matemáticas además de su método de cálculo de áreas?
-Además de su método de cálculo de áreas, Arquímedes aportó dos términos importantes a las matemáticas: el concepto de pi y el cálculo del área de una circunferencia.
¿Qué es el método de Arquímedes para calcular el área de una circunferencia?
-El método de Arquímedes para calcular el área de una circunferencia consiste en inscribir y circunscribir rectángulos dentro y fuera de la circunferencia y calcular el área de cada uno. Luego, se suman las áreas de los rectángulos inscritos y circunscritos y se dividen entre 2 para obtener el área de la circunferencia.
¿Cuál es el significado de 'inscritos' y 'circunscritos' en el contexto del método de Arquímedes?
-En el contexto del método de Arquímedes, 'inscritos' se refiere a los rectángulos que están dentro de la circunferencia, mientras que 'circunscritos' se refiere a los rectángulos que están tocando la parte exterior de la circunferencia.
¿Cómo se determinó la base de los rectángulos en el ejemplo del script?
-En el ejemplo del script, la base de los rectángulos se determinó arbitrariamente como un centímetro, tanto para los rectángulos inscritos como para los circunscritos.
¿Cuántos rectángulos inscritos y circunscritos se utilizaron en el ejemplo del script para calcular el área de la circunferencia?
-En el ejemplo del script, se utilizaron nueve rectángulos inscritos y diez rectángulos circunscritos para calcular el área de la circunferencia.
¿Cuál fue el resultado del cálculo empírico del área de la circunferencia utilizando el método de Arquímedes en el ejemplo del script?
-El resultado del cálculo empírico del área de la circunferencia utilizando el método de Arquímedes en el ejemplo del script fue de 76.3 centímetros cuadrados.
¿Cuál es la fórmula teórica para calcular el área de una circunferencia y cuál fue el resultado en el ejemplo del script?
-La fórmula teórica para calcular el área de una circunferencia es pi multiplicado por el radio al cuadrado. En el ejemplo del script, el resultado utilizando esta fórmula fue de 78.54 centímetros cuadrados.
¿Cómo se compara el resultado del método empírico de Arquímedes con la fórmula teórica para el área de una circunferencia?
-El resultado del método empírico de Arquímedes (76.3 cm²) se compara con la fórmula teórica (78.54 cm²) para observar la similitud y la precisión del método antiguo en comparación con la fórmula moderna.
¿Quiénn investigadores y matemáticos posteriores se mencionan en el script como continuadores del trabajo de Arquímedes?
-En el script se mencionan a Newton, Leibniz, Barrow y Riemann como investigadores y matemáticos posteriores que continuaron el trabajo de Arquímedes.
¿Cuál es la relevancia de los sumatorios (suma griega sigma) en el método de Arquímedes para calcular áreas?
-La relevancia de los sumatorios en el método de Arquímedes es para agregar todas las áreas de los rectángulos inscritos y circunscritos, lo cual es fundamental para estimar el área de la circunferencia.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Suma de Riemann, paso a paso, MUY FÁCIL
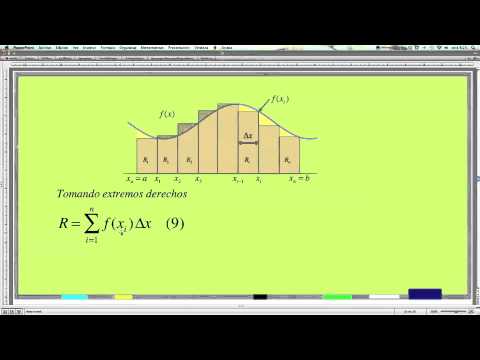
Calculo Integral 04: La integral definida. The definite integral.

Resolver una Suma de Riemann paso a paso. #MateYisus

Análisis Matemático II - Teorema Fundamental de Cálculo Integral - Parte 3

La integral: qué es, de dónde surge y para qué sirve
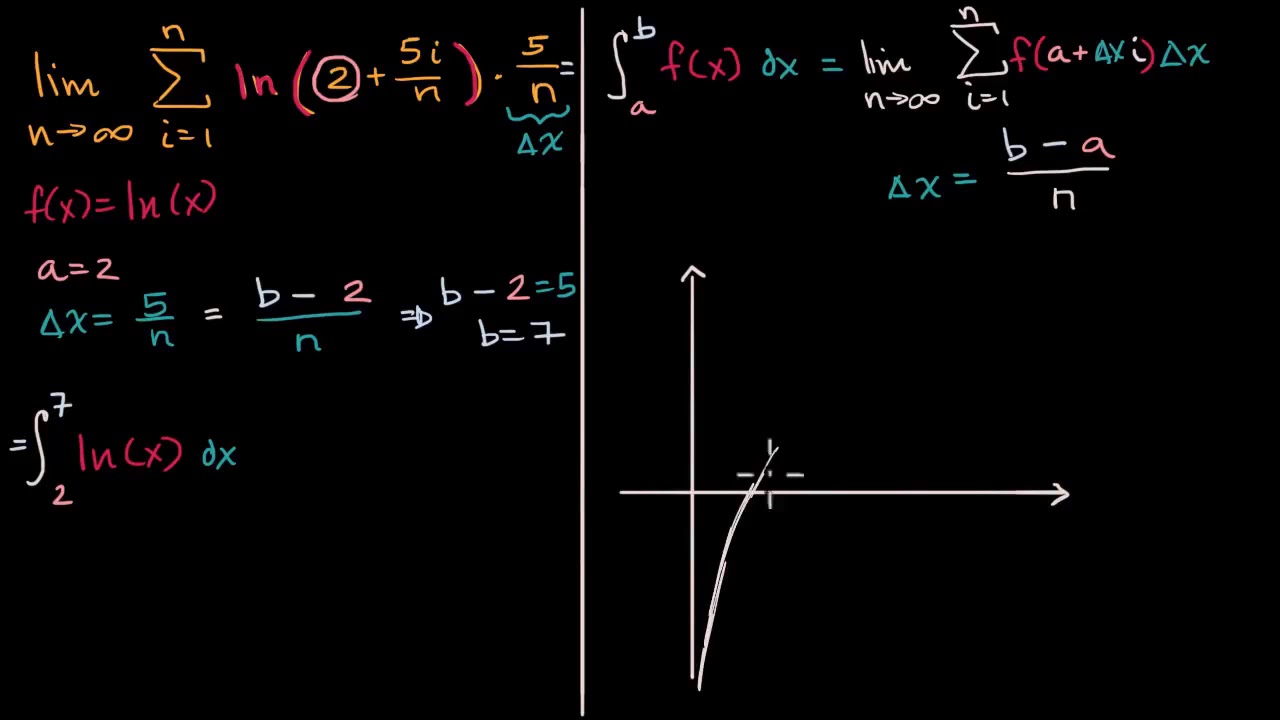
Escribir el límite de una suma de Riemann como una integral definida | Khan Academy en Español
5.0 / 5 (0 votes)
