Representations of Rational Function

Summary

This lesson focuses on rational functions, teaching how to represent them through equations, tables of values, and graphs. It introduces the simplest form, f(x) = 1/x, and demonstrates creating a table with various x values, including handling undefined cases. The script then illustrates graphing the function, highlighting the concept of asymptotes. It further applies this knowledge to model real-life situations, such as a runner's speed over time, and concludes with a bonus discussion on transforming graphs of rational functions, including shifts and reflections, enhancing understanding of their behavior.

Takeaways

• 📚 The lesson's main objective is to understand how to represent a rational function through its equation, table of values, and graph.
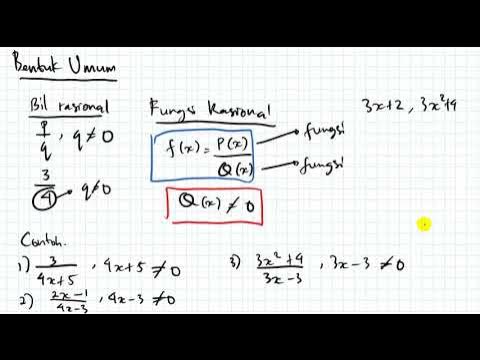
• 🔍 A rational function is defined as a function of the form f(x) = P(x) / Q(x), where P(x) and Q(x) are polynomials and Q(x) ≠ 0.
• 📈 The simplest rational function example given is f(x) = 1/x, which requires considering values for x that are negative, zero, and positive.
• 📊 To create a table for a rational function, substitute values of the independent variable into the function's equation and calculate the corresponding dependent variable values.
• 📉 The graph of a rational function will have vertical asymptotes where the denominator is zero, and these are represented by dashed lines on the graph.
• 🏃‍♂️ An example of a real-life application of a rational function is modeling the speed of a runner over time, with the function S(t) = 100 / t.
• 📝 When graphing, only positive values for time are considered since time cannot be negative.
• 📉 The graph of the runner's speed function will show how speed decreases as time increases.
• 🔄 Transformations of rational functions can involve horizontal shifts (changing the asymptote) and vertical shifts of the graph.
• 🔄 Changes in the denominator of a rational function can result in vertical shifts of the graph, while changes in the numerator can result in horizontal shifts.
• 📈 The graph of 1/x² is an example where the function does not have a negative denominator, and the graph is flipped on the x-axis compared to 1/x.
• 📚 The lesson concludes with a summary of how to represent rational functions and an invitation to check understanding through practice.

Q & A

What is the main objective of the lesson discussed in the transcript?

The main objective of the lesson is to represent a rational function through its equation, table of values, and graph, and as a bonus, to discuss how to transform graphs of rational functions.

What is a rational function in mathematical terms?

A rational function is a function of the form f(x) = P(x) / Q(x), where P(x) and Q(x) are polynomial functions and Q(x) is not equal to zero.

Why is it important to include negative, zero, and positive values when creating a table for a rational function?

Including negative, zero, and positive values ensures that the behavior of the rational function is understood across the entire domain, except where the function is undefined (e.g., division by zero).

What is an asymptote and why is it significant in the graph of a rational function?

An asymptote is a line that a graph approaches but never intersects. It is significant in the graph of a rational function because it indicates the values that the function approaches as the independent variable approaches infinity or negative infinity.

How does the value of a function become undefined in the context of rational functions?

The value of a function becomes undefined when the denominator of the rational function is zero, as division by zero is undefined in mathematics.

What is the world record for the 100-meter dash as mentioned in the transcript, and who holds it?

The world record for the 100-meter dash, as of October 2015, is 9.58 seconds, set by the Jamaican sprinter Usain Bolt.

How is the speed of a runner represented as a function of time in the transcript?

The speed of a runner is represented as a function of time by the equation S(T) = 100 / T, where S is the speed and T is the time taken to run 100 meters.

What is the significance of the vertical dashed line in the graph of the function S(T)?

The vertical dashed line in the graph of the function S(T) represents the time at which the speed would be undefined, which in this case is when T equals zero, as time cannot be negative.

What happens to the horizontal asymptote when a constant is added to the numerator of a rational function?

When a constant is added to the numerator of a rational function, the graph of the function moves vertically by the same amount, and the horizontal asymptote also shifts by that constant value.

What is the effect of adding a constant to the denominator of a rational function on the graph and its vertical asymptote?

Adding a constant to the denominator of a rational function shifts the graph horizontally. The vertical asymptote moves to the left by the absolute value of the constant if it's positive, or to the right if it's negative.

How does the exponent of the variable in the denominator affect the graph of a rational function?

If the exponent of the variable in the denominator is even, the graph will not extend into the negative y-values, effectively flipping the lower half of the graph onto the x-axis.

What is the process of transforming the graph of the function f(x) = 1/x^2 when a constant is added to the function?

When a constant is added to the function f(x) = 1/x^2, the graph moves vertically upward by the value of the constant. For example, if the function is g(x) = 1/x^2 + 2, the graph of g will be 2 units higher than that of f.

How does the graph of a rational function change when a constant is subtracted from the variable in the denominator?

When a constant is subtracted from the variable in the denominator of a rational function, the graph moves horizontally to the right by the absolute value of the constant.

What is the final step in the process of representing a rational function through its equation, table of values, and graph?

The final step is to connect the points plotted on the graph to visualize the behavior of the rational function, including its approach to any asymptotes.

Outlines

00:00

📚 Introduction to Rational Functions

This paragraph introduces the lesson's main objective, which is to represent a rational function using its equation, table of values, and graph. It also briefly mentions a bonus discussion on graph transformations. The paragraph begins by identifying various types of functions and focusing on the rational function, defined as a ratio of two polynomial functions where the denominator is non-zero. The simplest example, f(x) = 1/x, is used to demonstrate creating a table of values with negative, zero, and positive values for x. The paragraph concludes with an introduction to graphing the function, including handling undefined values and the concept of asymptotes.

05:05

🏃‍♂️ Applying Rational Functions to Real-Life: Runner's Speed

The second paragraph applies the concept of rational functions to model the speed of a runner over time in a 100-meter dash. It defines the function s(T) = 100/T, where T represents time in seconds. The paragraph explains why only positive values are considered for time and demonstrates how to create a table of values for various time intervals. It then proceeds to graph the function, illustrating how to plot points and connect them to form the function's graph. The discussion includes the concept of horizontal asymptotes and references further learning on function transformations.

10:06

📉 Transforming Rational Functions: Vertical and Horizontal Asymptotes

This paragraph delves into the transformations of rational functions, focusing on how changes in the function's equation affect its graph, specifically the movement of vertical and horizontal asymptotes. It provides examples of how adding or subtracting values in the numerator or denominator affects the graph's position and the asymptotes' equations. The paragraph explains the implications of even powers in the denominator, which eliminate the negative range and flip the graph on the x-axis. It concludes with a summary of the transformations discussed and encourages viewers to apply these concepts to practice graphing.

15:08

📈 Graphing and Completing a Table for a Given Rational Function

The final paragraph presents a practical exercise in completing a table for a given rational function and graphing it. It demonstrates the process of substituting values into the function T(x) = 1/(x+3)(x-3), handling undefined values, and plotting the resulting points on a graph. The paragraph also shows how to connect the plotted points to form the function's graph, indicating the approach towards asymptotes. It concludes with a preview of the next lesson's topic, which is the domain and range of rational functions.

Keywords

💡Rational Function

A rational function is a mathematical expression that is the ratio of two polynomials, where the denominator is not equal to zero. In the video, the theme revolves around representing and understanding rational functions through their equations, tables of values, and graphs. An example given is f(x) = 1/x, which is the simplest form of a rational function and is used to demonstrate how to create a table of values and graph the function.

💡Polynomial

A polynomial is an algebraic expression made up of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents. In the context of the video, polynomials are the building blocks of rational functions, with the function f(x) = B(x)/Q(x) where both B(x) and Q(x) are polynomials.

💡Table of Values

A table of values is a method used to organize and display the output of a function for various input values. In the video, creating a table of values for the rational function f(x) = 1/x helps to visualize the function's behavior, such as the approach to infinity as x approaches zero from the positive side.

💡Graph

In the video, graphing is the visual representation of a function's equation. The script describes how to plot points from the table of values onto a Cartesian plane to form the graph of a rational function, illustrating its behavior and any asymptotic behavior.

💡Asymptote

An asymptote is a line that a graph approaches but never intersects. The video explains vertical asymptotes, such as x = 0 for the function f(x) = 1/x, and how they are represented on the graph with a dashed line. Asymptotes are crucial in understanding the limits of a function's values.

💡Independent Variable

The independent variable is the input value that can be freely chosen in a function. In the video, x is the independent variable for the rational function, and different values of x are substituted into the function to determine the corresponding dependent variable values.

💡Dependent Variable

The dependent variable is the output value determined by the function based on the independent variable. In the script, the dependent variable is the value of the function f(x) for a given x, illustrating how the function's value changes with different inputs.

💡Transformation

Transformation refers to the process of modifying a graph or function in a certain way, such as shifting, stretching, or reflecting. The video discusses how adding or subtracting terms to the numerator or denominator of a rational function can transform its graph, affecting its position and asymptotes.

💡Horizontal Asymptote

A horizontal asymptote is a horizontal line that a graph approaches as the function's input (x) approaches infinity or negative infinity. The video explains how changes to the numerator of a rational function can result in a horizontal shift of the asymptote, as demonstrated with the function f(x) = 1/x + 2.

💡Vertical Asymptote

A vertical asymptote is a vertical line where the function is undefined, typically occurring when the denominator of a rational function is zero. The video script describes how changes to the denominator can result in a vertical shift of the asymptote, as shown with the function f(x) = 1/(x + 2).

💡Exponent

An exponent indicates the number of times a base is multiplied by itself. In the context of the video, when the exponent is applied to the variable x in the denominator, it affects the graph's behavior, as seen with the function f(x) = 1/x^2, which lacks a vertical asymptote and has a different graph shape compared to f(x) = 1/x.

Highlights

The main objective of the lesson is to understand the representation of rational functions through equations, tables of values, and graphs.

Bonus discussion on transforming graphs of rational functions is introduced.

A rational function is defined as a function where the numerator and denominator are polynomials, with the denominator not equal to zero.

The simplest rational function, f(x) = 1/x, is used to demonstrate creating a table of values with various x values.

The importance of including negative, zero, and positive values for the independent variable in table creation is emphasized.

The concept of an undefined function value at x = 0 for the function 1/x is explained.

A vertical asymptote at x = 0 for the function 1/x is graphically represented with a dashed line.

The process of graphing rational functions by plotting points and connecting them is demonstrated.

An example of modeling real-life situations with rational functions, such as the speed of a runner over time, is presented.

The creation of a table for the runner's speed function, s(t) = 100/t, is shown with positive time values only.

The graphical representation of the runner's speed function, showing its behavior as time increases, is provided.

The concept of horizontal asymptotes in rational function graphs is introduced.

The effect of adding a constant to the numerator on the horizontal asymptote is explained.

The impact of subtracting a constant from the denominator on the vertical position of the graph and its asymptote is discussed.

The transformation of the vertical asymptote when a constant is added to the denominator is illustrated.

The absence of a vertical asymptote in the graph of 1/x^2 due to the even exponent is noted.

The transformation of the graph of 1/x^2 when a constant is added to the numerator is shown.

The effect of adding a constant to the denominator on the horizontal movement of the graph and its asymptote is described.

The summary of the lesson on representing rational functions and a prompt for students to check their understanding concludes the transcript.

Transcripts

our main objective for this lesson is to

represent a rational function through

its equation table of values and graph

as a bonus I am also going to discuss

how to transform graphs of rational

functions let's have a quick activity

let us identify the following function

this is a cubic function

this one is a logarithmic function

this is a linear function

this one is a trigonometric function

while this one is a quadratic function

and the last but not the least is the

rational function

today's discussion will focus on the

rational function

you have learned that a rational

function is a function of the form f of

x is equal to B of X over Q of X where P

of x and q of X are polynomial functions

and Q of X is not equal to zero here are

some examples we have the name of the

function here

an equal sign

and a polynomial divided by a polynomial

where the denominator is not equal to

zero probably the simplest rational

function is f of x equals 1 over X

remember that in a function there is an

independent variable and the dependent

variable the dependent variable relies

only on the value of the independent

variable let us create a table for this

in assigning values for independent

variable I suggest that you should have

negative values 0 and positive values

all you have to do is to substitute each

value of x in our equation so in this

case this would be 1 divided by negative

four so we have negative 1 4. next one

let us substitute negative 3 here so

this will become 1 divided by negative

3. next one is negative 2 so this is 1

divided by negative 2. then we have

negative 1 here 1 divided by negative

one is negative one let us substitute

zero in our denominator 1 divided by

zero will become

undefined let us substitute one here one

divided by one is one

substituting 2 1 divided by 2 or 1 half

let us substitute 3 1 divided by 3 or 1

3 and let us substitute four one divided

by 4 is 1 4. this time let us represent

our function through a graph let's have

our Cartesian plane all we have to do is

to plot the points that we have here if

our X is negative 4

our f of x or y is negative one fourth

so here is negative four and then

negative 1 4 is somewhere here

and then we have negative 3 for x and

negative 1 3 for f of x somewhere here

then we have negative 2 for x and

negative one-half right at the middle of

zero and negative one

then we have negative one negative one

negative one negative one

if our X is zero the value of the

function is undefined meaning we do not

have graph at x equals zero let me graph

a vertical dashed line here this is

called asymptote you will learn more

about this in our succeeding lessons

then we have here one One X is one y is

one

if our X is 2 our Y is one half at the

middle of zero and one

if our X is 3 then our Y is one third

somewhere here

and if our X is 4 our Y is 1 4 somewhere

here

now let us graph this this one is

approaching this blue vertical line here

the asymptote and this one is also

approaching this blue vertical line here

going down so now we were able to

represent our function through an

equation table of values and a graph a

function is used to model or represent

real life situation to give you an

example

the current world record as of October

2015 for the 100 meter dash is 9.58

seconds set by the Jamaican Usain Bolt

in 2009 let us represent the speed of a

runner as a function of the time it

takes to run 100 meters in the truck

name the function s and the variable T

the name of the function is s and the

variable is T so we have S of t as here

represents the speed and we have learned

from physics that is speed is distance

over time the distance is already given

it is 100 and the time is the variable T

so we have S of T is equal to 100

divided by T now let us create a table

for this you might ask me why I do not

have negative values support B for the

independent variable it is because we do

not have negative seconds of time we

only have positive values for the time

so again we just have the substitute our

T in the equation so 100 divided by the

first value of T which is 10 100 divided

by 10 is equal to 10 then we have 100

divided by 12 is equal to 8.33 100

divided by 14 is 7.14

100 divided by 16 is 6.25

100 divided by 18 is 5.36 and 100

divided by 20 is 5. next let us graph

this table

let us recall our function and the table

T here again is our independent variable

and it is plotted along the x-axis while

s of T is our dependent variable and it

is plotted along the y-axis let us start

if T is 10

our s of D is also 10 so we have our

Point here

if our D is 12 our s of D is 8.33

somewhere here if our T is 14 our s of T

is 7.14 somewhere here

if our T is 16 our s of D is

6.25 somewhere here

if our T is 18 our s of T is 5.56

and if our D is 20 our s of T is equal

to 5. now let us connect these points so

again we were able to represent our

function through an equation table of

values and a graph as a bonus like what

I've said earlier allow me to discuss

how to transform rational functions for

better understanding please watch my

video on kinds of functions and its

transformation we have learned that this

graph is f of x equals 1 over X our

horizontal asymptote here is y equals

zero now what if we have P of X is equal

to 1 over X plus two the only difference

of these two is the additional plus 2

here this graph will now move two units

up

so this horizontal asymptote y equals 0

will also move this is now y equals

positive 2. now what if we have q of X

is equal to 1 over x minus 2 so again

the only difference here this time is

negative 2 so the original function will

now move two units down

so this horizontal asymptote will also

move two units down

the equation of this asymptote now is y

equals negative 2. now try this again

this is f of x is equal to 1 over X this

time I want you to focus on the vertical

asymptote the equation of this asymptote

is x equals zero what if I have B of X

is equal to 1 over X plus 2. the only

difference of these two is the positive

2 here in the denominator if this is the

case our matter function will now move

going to the left

by how many units by two units so this

vertical asymptote will also move two

units going to the left and the equation

of this will become x equals negative 2.

now what if I have q of X is equal to 1

divided by x minus 2. this time I have

minus 2 added in the denominator the

original function now will move two

units going to the right so this

vertical asymptote will also move two

units going to the right the equation of

this asymptote will now become x equals

2. let's have another rational function

we already know the graph of f of x

equals 1 over x what if we have P of x

equals 1 over x squared so notice the

difference we have here the X exponent

2. if that is the case it means we will

not have a negative denominator because

a negative number raised to an even

exponent will just become positive so it

means we do not have graph down here

this graph down here will flip on the

x-axis so it will now become here on top

so the graph of 1 over x squared looks

like this let us transform this graph

what if I have this graph what will be

the equation of this graph the only

difference it move two units up let me

use another name for the function for

this graph so the graph move two units

up so the mother function will have plus

2 at the right so I have V of x equals 1

over x squared plus 2. now what if I

have a graph like this from the mother

function you will see that the graph

move two units to the right so the

changes in our equation will occur in

our denominator again let me use another

name for this function it will become 1

over x minus 2 quantity squared remember

that if you have minus 2 in the

denominator the graph moves to the right

by how many units by two units now what

if we have a graph like this so the

graph move up and also to the left how

many units did it move upward 1 2 3 then

how many units it move to the left from

here 1 2 let me use another name for

this graph the name will be T of X is

equal to 1 over X plus 2 quantity

squared plus 3 since it move 3 units up

for the summary I hope you have learned

how to represent rational function

through its equation table of values and

graph now it is time to check your

understanding pause this video for more

time

thank you

let us answer we are asked to complete

the table and then graph the function so

let us substitute negative 1 here

negative 1 plus 3 will give us 2

negative 1 minus 3 will give us negative

4 2 over negative 4 will give us

negative one-half let us substitute zero

here zero plus three is three zero minus

three is negative three three divided by

negative three is negative one let us

substitute one here one plus three is

four one minus three is negative two

four divided by negative two is negative

two let us substitute two here two plus

three is five two minus three is

negative one five divided by negative

one is negative five let us substitute

three here three plus three is six three

minus three is zero so if our X is three

our denominator will become zero and a

number divided by zero is undefined next

let us substitute 4 here 4 plus 3 is 7.

4 minus three is one seven over one is

seven let us substitute five five plus

three is eight five minus three is two

eight divided by two is four and let us

substitute six six plus three is nine

six minus three is three nine divided by

three is three now that we have

completed the table let us graph if our

X is negative one our Y is negative one

half so somewhere here

if our x is 0 our Y is negative one if

our X is 1 our Y is negative 2. if our X

is 2 our Y is negative five if our X is

3 then we have undefined meaning we do

not have graph at x equals three allow

me to create a vertical dashed line if

our X is 4 our Y is equal to seven

somewhere here

if our X is 5 our Y is equal to 4. and

if our X is 6 our Y is equal to 3. now

let us connect the points

so this graph is approaching this

asymptote and this graph is also

approaching this asymptote gets our next

lesson is domain and range of rational

functions