ANIMATED CONIC SECTION

EduTech TV

28 Sept 202007:05

Summary

TLDRThis tutorial video delves into the fascinating world of conic sections, exploring their generation from the intersection of a plane with two cones. It explains the formation of an ellipse when the plane is not parallel to the cone's base, a parabola when it cuts through one cone's base, and a hyperbola when slicing through both. Special attention is given to the degenerate cases, including points, lines, and intersecting lines, formed under specific cutting conditions. The video concludes by summarizing the four primary conic sections and their unique characteristics.

Takeaways

📚 The script introduces the concept of conic sections and their generation from the intersection of a plane with two cones.
📏 The figure formed by the intersection of a vertical line and another line is called a double knob right, circular cone, with the vertical line being the axis and the point of intersection the vertex.
🔍 The two distinct lines on the cone are known as the generators, and the two circles formed are the bases of the cone.
🌀 The parts of the cone referred to as 'lowering up' and 'upper nap' are described, though the exact terms may be misheard or misspoken in the script.
🔪 The conic sections are formed by the intersection of a plane with the cones, with different results depending on the orientation and position of the plane relative to the cones.
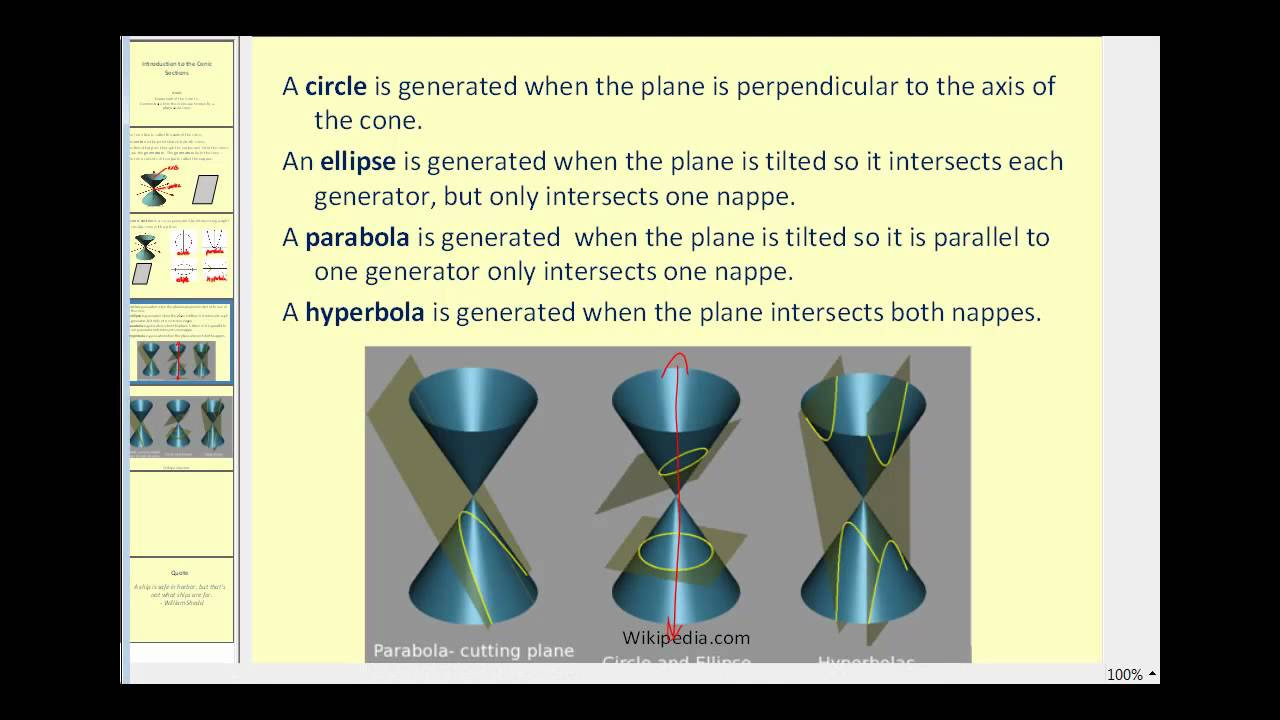
🌕 A circle is formed when the plane is parallel to the cone's base and passes through both cones.
🥚 An ellipse is created when the plane is not parallel to the base and does not pass through both bases.
🚀 A parabola is the result of a plane cutting through only one nap of the cone and passing through that cone's base.
🌌 A hyperbola is formed when the plane cuts through both naps of the cones and passes through the bases of both.
📝 The script summarizes the four conic sections as ellipse, circle, parabola, and hyperbola, with the circle being a special case of an ellipse.
📐 Degenerate cases are also discussed, where the plane's orientation and position relative to the cones result in figures such as a single point, a line, or intersecting lines.

Q & A

What is a conic section?
-A conic section is a curve obtained by intersecting a cone with a plane. It can result in an ellipse, a circle, a parabola, or a hyperbola, depending on the angle and position of the intersecting plane.
What are the four types of conic sections?
-The four types of conic sections are ellipse, circle, parabola, and hyperbola.
What is the special relationship between a circle and an ellipse?
-A circle is a special type of ellipse where the two axes of the ellipse are of equal length, making it perfectly round.
What is the term used for the line that intersects the vertical line to form a double-knob right circular cone?
-The line that intersects the vertical line to form a double-knob right circular cone is called the axis of the cone.
What are the generators of a cone?
-The generators of a cone are the two distinct lines that form the sides of the cone, connecting the vertex to the edges of the base circles.
What is the term for the part of the cone that is referred to as the 'lowering up' in the script?
-The term 'lowering up' seems to be a mispronunciation or error in the script; it likely refers to the 'lower nap' or the lower half of the cone.
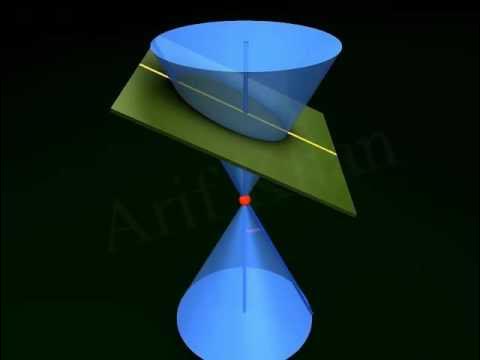
What happens when a plane is parallel to the bases of the cone and passes through the cones?
-When a plane is parallel to the bases of the cone and passes through the cones, it forms a circle.
What figure is formed when a cutting plane is not parallel to the base of the cone and does not pass through the bases?
-When a cutting plane is not parallel to the base of the cone and does not pass through the bases, an ellipse is formed.
What is a parabola?
-A parabola is a conic section formed when a plane cuts only one nap of the cone and passes through the base of that cone.
What is a hyperbola?
-A hyperbola is a conic section formed when a plane cuts both naps of the two cones and passes through the bases of the two cones.
What are the degenerate cases of conic sections?
-The degenerate cases of conic sections occur when the cutting plane is in a specific position relative to the cone, resulting in figures such as a point, a line, or two intersecting lines, instead of the typical conic sections.
What figure is formed when the cutting plane is parallel to the base of the cone and passes exactly at the vertex?
-When the cutting plane is parallel to the base of the cone and passes exactly at the vertex, the figure formed is just a point.
What happens when the cutting plane is parallel to the generator of the cone and passes through the vertex?
-When the cutting plane is parallel to the generator of the cone and passes through the vertex, the figure formed is a line.
What is the result when the plane cuts both naps of the cones and passes through the vertex?
-When the plane cuts both naps of the cones and passes through the vertex, the result is two intersecting lines.

Outlines

00:00

📚 Introduction to Conic Sections and Degenerate Cases

This paragraph introduces the concept of conic sections and their generation from a cone. It describes the formation of a double-knob circular cone when a line is rotated around a vertical axis, creating the vertex and the generators. The bases of the cone are two circles, and the parts above and below these bases are referred to as the 'lowering up' and 'upper nap' respectively. The paragraph then explains how different conic sections—circle, ellipse, parabola, and hyperbola—are formed by the intersection of a plane with the cones. The special case of a circle as a type of ellipse is also mentioned.

05:02

🔍 Exploring Degenerate Cases of Conic Sections

The second paragraph delves into the degenerate cases of conic sections, which occur under specific conditions of intersection between the cutting plane and the cone. When the cutting plane is parallel to the base of the cone and passes through the vertex, a single point is formed. If the cutting plane is parallel to the generator of the cone and also passes through the vertex, a straight line is the result. Lastly, when the plane cuts through both 'naps' of the cones and intersects at the vertex, two intersecting lines are formed. The summary concludes by reiterating the degenerate cases: a point, a line, and intersecting lines, corresponding to different orientations of the cutting plane relative to the cone.

Mindmap

Keywords

💡Conic Section

A conic section is a curve obtained as the intersection of a plane and a double-napped cone. The script introduces conic sections as the main theme of the video, explaining that they are formed by the intersection of a plane and a cone. Examples from the script include the circle, ellipse, parabola, and hyperbola, each resulting from different orientations of the intersecting plane.

💡Cone

A cone is a three-dimensional geometric shape with a circular base and a single vertex. In the context of the video, the cone is described as having a vertical axis and generators, which are the lines that define the shape of the cone. The script uses the cone to demonstrate how different conic sections are formed by slicing it with a plane.

💡Generators

In geometry, generators are the lines that define the surface of a cone, extending from the vertex to the circumference of the base. The script refers to these as the lines that form the double-knob figure when a line is rotated to create two cones.

💡Vertex

The vertex of a cone is the point where the two nap surfaces meet. The script describes the vertex as the central point of the cone from which the generators extend, and it is crucial in determining the orientation of the conic sections formed by slicing the cone.

💡Base

The base of a cone is the flat, circular surface at the bottom. In the script, the bases are the circles on the cone, and they are important in defining the conic sections, especially when the cutting plane is parallel to them, resulting in a circle.

💡Ellipse

An ellipse is a conic section formed when a plane intersects a cone at an angle that is not parallel to the base and does not pass through the vertex. The script explains that an ellipse is created when the cutting plane is not aligned with the base of the cone.

💡Parabola

A parabola is a conic section that results when a plane intersects one nap of the cone and passes through its base. The script illustrates this by showing that a parabola is formed when the plane cuts only one side of the cone and intersects the base.

💡Hyperbola

A hyperbola is a conic section formed when a plane intersects both nap surfaces of the cone and passes through the bases. The script describes the hyperbola as the figure formed when the plane cuts through both the upper and lower nap of the cone and its bases.

💡Degenerate Cases

Degenerate cases in the context of conic sections refer to the special instances where the intersection of the plane and cone does not result in one of the standard conic sections but rather in simpler geometric shapes like a point, line, or intersecting lines. The script provides examples of degenerate cases, such as when the plane is parallel to the base and passes through the vertex, resulting in a point.

💡Cutting Plane

The cutting plane in the script refers to the plane that intersects the cone to form conic sections. The orientation and position of the cutting plane determine the type of conic section produced, whether it be a circle, ellipse, parabola, or hyperbola.

💡Axis

In the context of the video, the axis of a cone is the vertical line around which the cone is formed. The axis is significant as it is the line that the cutting plane can be parallel or perpendicular to when forming conic sections.

Highlights

Introduction to conic sections and their generation by intersecting a plane with two cones.

Explanation of the double-knob right circular cone and its parts: axis, vertex, generators, bases, lower and upper nap.

Formation of a circle when a plane is parallel to the bases of the cones.

Observation of an ellipse when a cutting plane is not parallel to the cone bases and does not pass through both bases.

Formation of a parabola when a plane cuts only one nap of the cone and passes through its base.

Formation of a hyperbola when a plane cuts both naps of the cones and passes through the bases.

Summary of the four conic sections: ellipse, circle, parabola, and hyperbola, with the circle being a special type of ellipse.

Introduction to degenerate cases of conic sections.

Formation of a point in the degenerate case when the cutting plane is parallel to the cone base and passes through the vertex.

Formation of a line in the degenerate case when the cutting plane is parallel to the cone generator and passes through the vertex.

Formation of two intersecting lines in the degenerate case when the plane cuts both naps of the cones and passes through the vertex.

Summary of degenerate cases: point, line, and intersecting lines, based on the orientation and position of the cutting plane relative to the cones.

Visual representation of conic sections and degenerate cases through animated figures.

The importance of the cutting plane's orientation in determining the type of conic section or degenerate case formed.

The role of the cone's vertex and bases in the formation of conic sections and degenerate cases.

The mathematical concept of conic sections and their geometrical representation through intersecting planes and cones.

Educational tutorial providing a step-by-step explanation of conic sections and their generation.

Engaging musical background enhancing the learning experience throughout the tutorial.