Conic Section 3D Animation

Summary

This video explains the concept of conic sections, which are curves formed when a plane intersects a double right circular cone. The script covers the different types of conic sections—ellipse, parabola, and hyperbola—each formed by specific angles between the plane and the axis of the cone. It also discusses degenerate conics, where the plane intersects the cone at its vertex, leading to degenerate forms such as points or lines. The video offers a clear and concise explanation of how variations in the cutting angle result in different conic shapes, with circles as a special case of ellipses.

Takeaways

• 😀 A double right circular cone consists of two cones joined at a fixed point called the vertex.
• 😀 The line that rotates about the vertex to form the cone is called the generator, while the fixed line is called the axis.
• 😀 A right circular cone has a circular base and the axis is perpendicular to a line from the center of the base to the vertex.
• 😀 The perimeter of the base of a right circular cone is called the directrix, and the lateral surface is known as the nap.
• 😀 A double right circular cone has two naps: the upper nap above the vertex and the lower nap below the vertex.
• 😀 The angle between the generator and the axis of the cone is known as the vertex angle.
• 😀 Conic sections are two-dimensional curves formed when a plane intersects a double right circular cone in different ways.
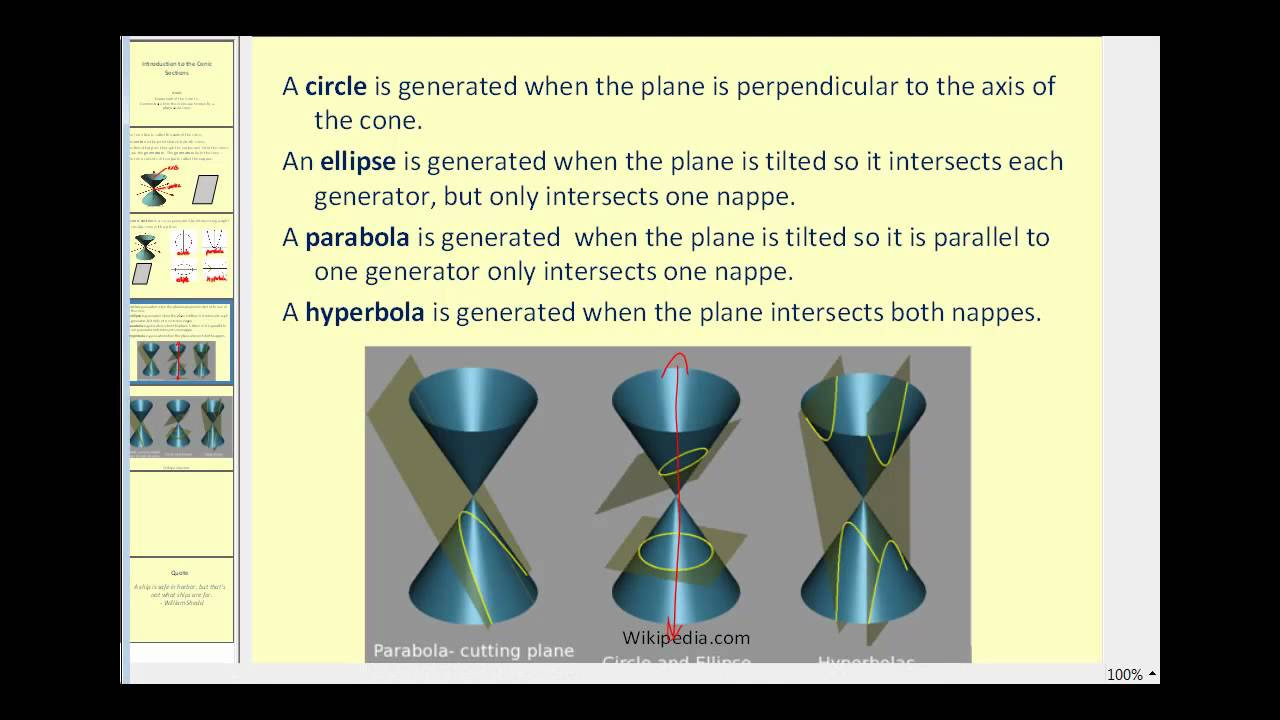
• 😀 An ellipse is formed when the plane cuts the cone with an angle greater than the vertex angle, creating a closed curve.
• 😀 A circle is a special type of ellipse, formed when the plane is perpendicular to the axis of the cone.
• 😀 A parabola is formed when the angle between the plane and the vertical axis of the cone is exactly equal to the vertex angle.
• 😀 A hyperbola is formed when the plane intersects both naps of the cone, creating two disjoint curves. A hyperbola can also be formed when the plane cuts only one nap, depending on the angle.

Q & A

What is a double right circular cone?

A double right circular cone is formed when a straight line intersects a vertical line at a fixed point and rotates about that point. It consists of two cones joined at the vertex.

What are the key components of a double right circular cone?

The key components of a double right circular cone include the vertex, the generator (the line that rotates), the axis (the fixed line), the base (circular), the directrix (perimeter of the base), and the naps (lateral surfaces of the cones).

What is the role of the generator in a right circular cone?

The generator is the rotating line that moves about the vertex to form the surface of the cone.

What are the two naps in a double right circular cone?

The two naps in a double right circular cone are the upper nap (above the vertex) and the lower nap (below the vertex).

What is the vertex angle in a double right circular cone?

The vertex angle is the angle between the generator and the axis of the cone.

What happens when a plane intersects a double right circular cone?

When a plane intersects a double right circular cone, it creates a two-dimensional curve known as a conic section, which can be an ellipse, parabola, or hyperbola depending on the angle of intersection.

How is an ellipse formed from a double right circular cone?

An ellipse is formed when the plane intersects the cone at an angle greater than the vertex angle but not perpendicular to the axis. If the plane is perpendicular to the axis, the ellipse becomes a circle.

What is the relationship between a circle and an ellipse?

A circle is a special case of an ellipse, where the plane intersects the cone perpendicular to the axis.

What defines a parabola in conic sections?

A parabola is formed when the plane intersects the cone at an angle equal to the vertex angle of the cone.

What is a hyperbola in conic sections?

A hyperbola is formed when the plane intersects both naps of the cone, with the angle between the plane and the axis being smaller than the vertex angle.

What are degenerate conics?

Degenerate conics are the figures formed when the plane intersects the double right circular cone at its vertex. These include a point (ellipse), a line (parabola), and two intersecting lines (hyperbola).