Mode, Median, Mean, Range, and Standard Deviation (1.3)
Summary
TLDRThis video script offers an insightful exploration of statistical measures such as mode, median, mean, range, and standard deviation. It explains how these measures provide numerical insights into data distribution, with the mode, median, and mean representing central tendency, and range and standard deviation indicating spread. The script elucidates the process of calculating each measure, emphasizing their significance in understanding data variability and distribution patterns, ultimately helping viewers grasp the concepts for effective data analysis.
Takeaways
- 📊 The video discusses statistical measures such as mode, median, mean, range, and standard deviation to describe data distribution.
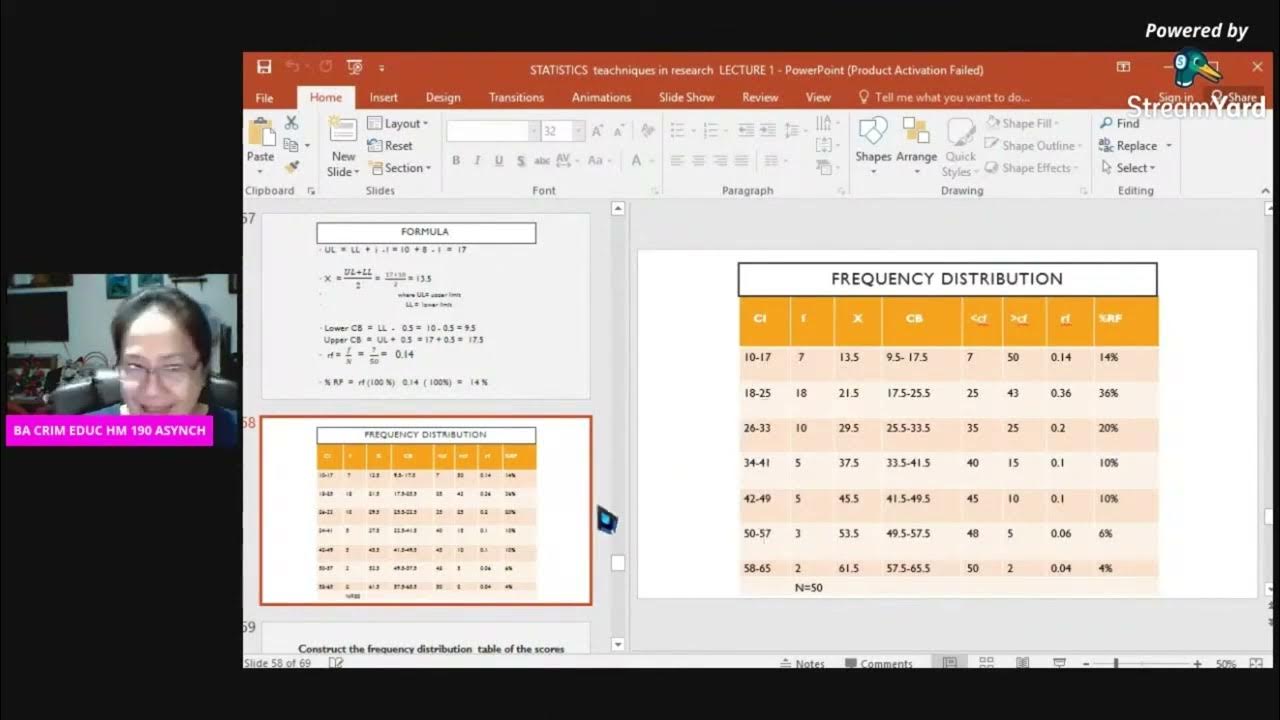
- 🔢 The mode is the most frequently occurring value in a dataset, exemplified by the number 154 appearing thrice in the sample.
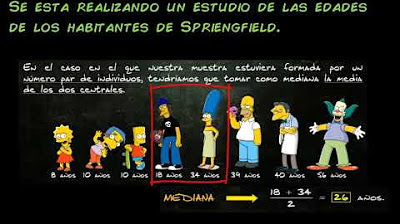
- 🎯 The median is the middle value of an ordered dataset, which in the sample is also 154, with four values on either side.
- 📈 For large datasets, the median position can be found using the formula (n + 1) / 2, where n is the total number of data points.
- 🤹♂️ If n is even, the median is the average of the two middle values, as shown with the calculation of 154.5 for the sample.
- 🧮 The mean, or arithmetic average, is calculated by summing all data values and dividing by the total number of values, resulting in 165.6 for the sample.
- ⚖️ The mean and median are both measures of central tendency but represent the center in different ways; the mean is a balance point, while the median is the physical middle.
- 📏 The range is a measure of spread, calculated by subtracting the minimum value from the maximum value, resulting in 57 for the sample.
- 💠 The standard deviation is a measure of how spread out the values are around the mean, calculated using a specific formula and resulting in 4.336 for the sample.
- 🔍 A small standard deviation indicates less variability and values closer to the mean, while a large standard deviation indicates more variability and values further from the mean.
- 📐 Variance is closely related to standard deviation, differing only in that variance does not involve taking the square root of the calculations.
Q & A
What are the numerical measures used to describe a data set's distribution?
-The numerical measures used to describe a data set's distribution are mode, median, mean, range, and standard deviation.
What is the mode of a data set?
-The mode is the data value that appears most frequently in a data set. For example, if the number 154 appears three times in a data set, it is the mode.
How do you find the median of a data set?
-To find the median, first order the data set from smallest to largest. The median is the middle value when the data set is ordered. If there is an odd number of data points, the median is the middle one. If there is an even number, the median is the average of the two middle values.
What is the formula used to find the median's position in a data set with an odd number of values?
-The formula to find the median's position in a data set with an odd number of values is (n + 1) / 2, where n is the total number of data values.
How is the mean of a data set calculated?
-The mean, or arithmetic average, is calculated by summing all data values and dividing by the total number of data values. If the mean is from a sample, it is denoted as X-bar.
What is the difference between the median and the mean?
-The median is the middle value of an ordered data set, while the mean is the average of all data values. The median represents the physical middle point, whereas the mean represents the balance point if the data values were of equal weights.
What does the range of a data set represent?
-The range represents the spread of a data set by subtracting the smallest value from the largest value, indicating how much 'room' the distribution takes.
How is the standard deviation calculated?
-The standard deviation is calculated using a formula that involves subtracting the mean from each data value, squaring the results, summing these squared differences, and then dividing by the total number of data values. The result is then taken as the square root to give the standard deviation.
What does a small standard deviation indicate about a data set?
-A small standard deviation indicates that the data values are close to the mean, suggesting less variability and a more concentrated distribution.
What is the relationship between variance and standard deviation?
-Variance is closely related to standard deviation. The only difference is that variance does not involve taking the square root of the calculations, whereas standard deviation does.
How do you denote sample variance and sample standard deviation?
-Sample variance is denoted as 's squared' (s^2), and sample standard deviation is denoted as 's'.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тариф5.0 / 5 (0 votes)