Lesson 1 - Laplace Transform Definition (Engineering Math)
Summary
TLDRIn this comprehensive tutorial series, Jason introduces students to the LL (Laplace) transform, a powerful mathematical tool used in science and engineering to solve differential equations more efficiently. Starting with the basics, the course builds up to using a table of LL transforms and properties for both direct and inverse transformations. The script emphasizes the practicality of the LL transform in various fields and guides learners through the process of transforming functions of time into the S domain, showcasing the transform's utility in simplifying complex problems.
Takeaways
- 📚 The course is designed to teach students how to master the use of the Laplace Transform, starting from scratch and building up to practical applications.
- 🔧 The Laplace Transform is a powerful tool used in science and engineering to solve complex problems, particularly differential equations, more efficiently.
- 📈 The course covers the Laplace Transform properties and how to apply both forward and inverse transforms to functions of time.
- 🎓 Students are expected to have basic knowledge of calculus and algebra, as these are fundamental to understanding and performing the Laplace Transform calculations.
- ⏳ The Laplace Transform takes a function of time and transforms it into a function in the 'S-domain', simplifying the process of solving differential equations.
- 📉 The integral definition of the Laplace Transform involves integrating a function of time multiplied by an exponential function over time from 0 to infinity.
- 📑 A table of common Laplace Transforms is an essential resource that students will learn to apply and derive, starting with simple functions and building up to more complex ones.
- 🌟 The Laplace Transform of an exponential function e^(λt) is particularly important and results in a simple function of 's', which is 1 / (s - λ), provided s > λ.
- 🔄 The Laplace Transform can be applied in a wide range of scientific and engineering disciplines, including electrical circuits, mechanical systems, and aerospace engineering.
- 📝 The process of solving problems with the Laplace Transform involves transforming the problem into the S-domain, solving it there with simpler algebraic methods, and then transforming the solution back to the time domain.
- 📚 The special case of the Laplace Transform when λ = 0, which is the transform of the constant function 1, results in 1 / s, valid for s > 0.
Q & A
What is the main objective of the LLas Transform Tutor course?
-The main objective of the LLas Transform Tutor course is to build students' skills so that they can master the use of the LLas transform, including how to use a table of LL transforms and the properties of the LLas transform to perform both direct and inverse transformations.
Why are LLas transforms important in science and engineering?
-LLas transforms are important in science and engineering because they provide a practical skill used to solve more complicated problems in various classes, including electrical engineering, mechanics, pure mathematics, and differential equations. They simplify the process of solving differential equations, which are ubiquitous in these fields.
What mathematical background is expected from students before starting the LLas Transform course?
-Students are expected to have a basic understanding of calculus, ideally at the level of 'calculus one', and proficiency in algebra. This background will enable them to perform the mathematical operations required for the LLas transform.
What is the basic concept behind the LLas transform?
-The basic concept behind the LLas transform is to take a function of time (or any function) and transform it into a new function in a different domain (the S domain), simplifying the process of solving differential equations and other complex problems.
How does the LLas transform help in solving differential equations?
-The LLas transform helps in solving differential equations by providing a unified method to convert a complex differential equation into a new form in the S domain, which is often easier to solve using algebraic methods. Once solved, the solution can be transformed back into the time domain.
What is the mathematical expression for the LLas transform of a function F(t)?
-The mathematical expression for the LLas transform of a function F(t) is given by the integral from 0 to infinity of e to the minus s t * F of t with respect to t, denoted as F(S) = L{F(t)} = ∫[0,∞] e^(-st) * F(t) dt.
What is an improper integral, and how is it related to the LLas transform?
-An improper integral is an integral where at least one of the limits is infinity, or the integrand has an unbounded point in the interval of integration. In the context of the LLas transform, the improper integral is used to transform a time-domain function into the S domain.
What is the significance of the LLas transform of an exponential function e^(Λt)?
-The LLas transform of an exponential function e^(Λt) is significant because it results in a simple function of S, which is 1 / (s - Λ). This result is a fundamental part of the LLas transform table and is used as a basis for transforming more complex functions.
What is the LLas transform of the constant function '1'?
-The LLas transform of the constant function '1' is 1 / s, which is derived from the special case of the exponential function e^(Λt) when Λ equals zero.
Why is it necessary to consider the condition 'S greater than Λ' when discussing the LLas transform of e^(Λt)?
-The condition 'S greater than Λ' ensures that the denominator in the resulting function of S from the LLas transform does not become zero, thus avoiding undefined or infinite values in the transform.
Can you provide an example of how the LLas transform simplifies the solution of a real-world problem?
-While the script does not provide a specific real-world example, the LLas transform simplifies real-world problems by allowing engineers and scientists to convert complex time-domain differential equations into simpler algebraic equations in the S domain. Solving these equations is typically more straightforward, and the solutions can then be transformed back to the time domain to provide practical solutions to real-world problems.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Transform Calculus and its applications in Differential Equations

Equações Diferenciais: Pra que Serve a Transformada de Laplace?

The Physics of Euler's Formula | Laplace Transform Prelude

Laplace Transform and Piecewise or Discontinuous Functions

Control Systems Lectures - Time and Frequency Domain
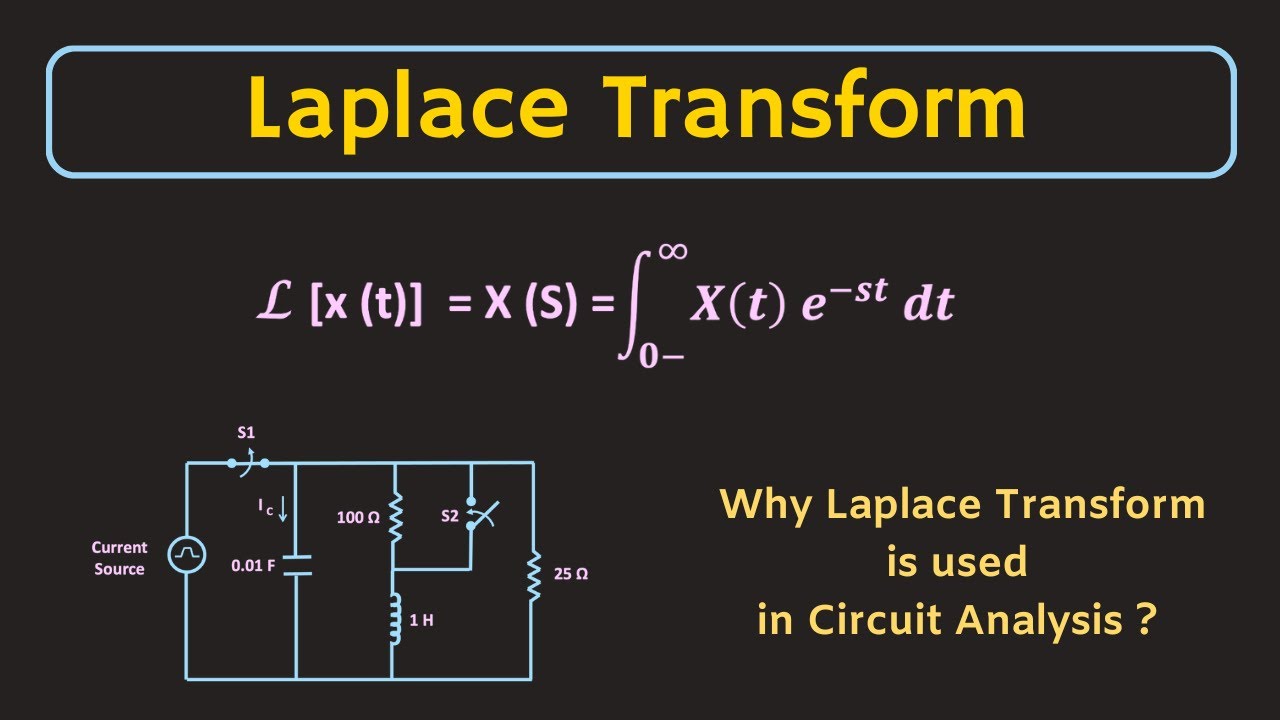
What is Laplace Transform? Why Laplace Transform is used in Circuit Analysis?
5.0 / 5 (0 votes)
