What is Laplace Transform? Why Laplace Transform is used in Circuit Analysis?

Summary

In this video, the concept of the Laplace Transform and its significance in circuit analysis is explained. The Laplace Transform is an integral tool that converts time-domain functions into the complex frequency domain, simplifying the process of solving differential equations in circuit analysis. The video highlights its advantages, such as converting convolutions into multiplications and accounting for initial conditions. The process of using the Laplace Transform to analyze RC, RL, and RLC circuits is covered, along with the formal definition and conditions for its use. The video also introduces the inverse Laplace Transform and its application in circuit analysis.

Takeaways

• 😀 Laplace transform is an integral transform that converts a time-domain signal into the complex frequency (S) domain.
• 😀 It is widely used in science and engineering to solve differential equations by converting them into algebraic equations.
• 😀 The Laplace transform helps simplify circuit analysis by converting complex differential equations into algebraic ones.
• 😀 It is especially useful for finding the transient response of RC, RL, and RLC circuits, even with non-standard excitations.
• 😀 Initial conditions of a system are automatically accounted for during the Laplace transform process, making it easier to find the total response of a circuit.
• 😀 The procedure for circuit analysis using Laplace transforms includes finding differential equations, applying the Laplace transform, solving algebraically in the S domain, and then taking the inverse Laplace transform to return to the time domain.
• 😀 The Laplace transform of a time-domain function, denoted as X(s), is expressed as the integral of x(t)e^(-st) dt from 0 to infinity.
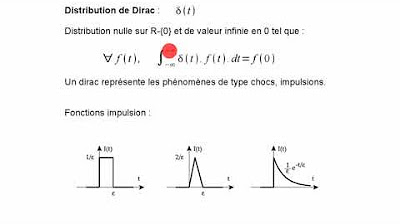
• 😀 Functions like delta functions or unit step functions, which have discontinuities at t=0, are handled using a '0 minus' limit in the Laplace transform.
• 😀 The region of convergence (ROC) for a Laplace transform is determined based on the real part of the S-domain variable (σ), which ensures the integration converges.
• 😀 A Laplace transform exists for functions if the integration of x(t)e^(-σt) from 0 to infinity is finite, and the real part of σ must satisfy specific conditions based on the function.
• 😀 For inverse Laplace transforms, a table of common functions and their transforms is often used in circuit analysis, rather than directly applying the inverse formula.
• 😀 The video will further explore the inverse Laplace transform process, its application in circuit analysis, and demonstrate practical examples.

Q & A

What is the Laplace transform and why is it used in circuit analysis?

The Laplace transform is an integral transform that converts a time-domain function into a complex frequency domain. It is used in circuit analysis to convert differential equations into algebraic equations, making it easier to solve circuits, especially those with complex signals or higher-order differential equations.

What is the general procedure for using Laplace transform in circuit analysis?

The general procedure involves first forming the differential equation of the circuit using KVL or KCL. Then, the Laplace transform is applied to convert the differential equations into algebraic equations. After algebraic manipulation in the S domain, the inverse Laplace transform is used to obtain the time-domain response of the circuit.

How does the Laplace transform simplify the analysis of differential equations?

The Laplace transform simplifies differential equations by converting them into algebraic equations, which are easier to solve. It also handles initial conditions in a single operation, reducing the complexity of solving for the circuit's response.

What is meant by the 'region of convergence' (ROC) in Laplace transforms?

The region of convergence (ROC) refers to the range of values for the real part of the complex frequency variable 'S' where the Laplace transform of a given function converges. It is important because it defines the conditions under which the Laplace transform exists for a particular function.

Why is the Laplace transform useful for handling non-standard excitations in circuits?

The Laplace transform is useful because it can handle non-standard excitations (e.g., step functions, impulses, etc.) by converting these time-domain functions into a form that is easier to work with algebraically in the S domain.

What is the significance of the complex frequency variable 'S' in the Laplace transform?

The complex frequency variable 'S' is used to represent the Laplace transform in the frequency domain. It is a combination of a real part (σ) and an imaginary part (jω), which allows the analysis of both the damping and oscillatory components of a system.

What is the one-sided Laplace transform, and why is it used in circuit analysis?

The one-sided Laplace transform is used when the function is defined only for t ≥ 0, which is typical in circuit analysis. It captures functions that start at t = 0 or after, such as unit step functions or impulse functions, and is the most commonly used Laplace transform for circuit analysis.

What does it mean for a function to be 'Laplace transformable'?

A function is Laplace transformable if its integration, when multiplied by e^(-st), converges and is finite over the time interval from 0 to infinity. This ensures that the Laplace transform can be applied to the function and the result will be meaningful.

What is the inverse Laplace transform, and how is it related to the Laplace transform?

The inverse Laplace transform is the process of converting a function in the S domain (frequency domain) back to the time domain. It is performed by integrating over a line in the complex S plane, typically within the region of convergence, to retrieve the original time-domain function.

How do basic properties of the Laplace transform help in circuit analysis?

The basic properties of the Laplace transform, such as linearity, shifting in time, and the ability to handle initial conditions, help simplify circuit analysis by allowing for the transformation of complex time-domain behavior into simpler algebraic expressions in the S domain. This leads to faster and more efficient solutions for circuit problems.