Circles - Chords, Radius & Diameter - Basic Introduction - Geometry

Summary

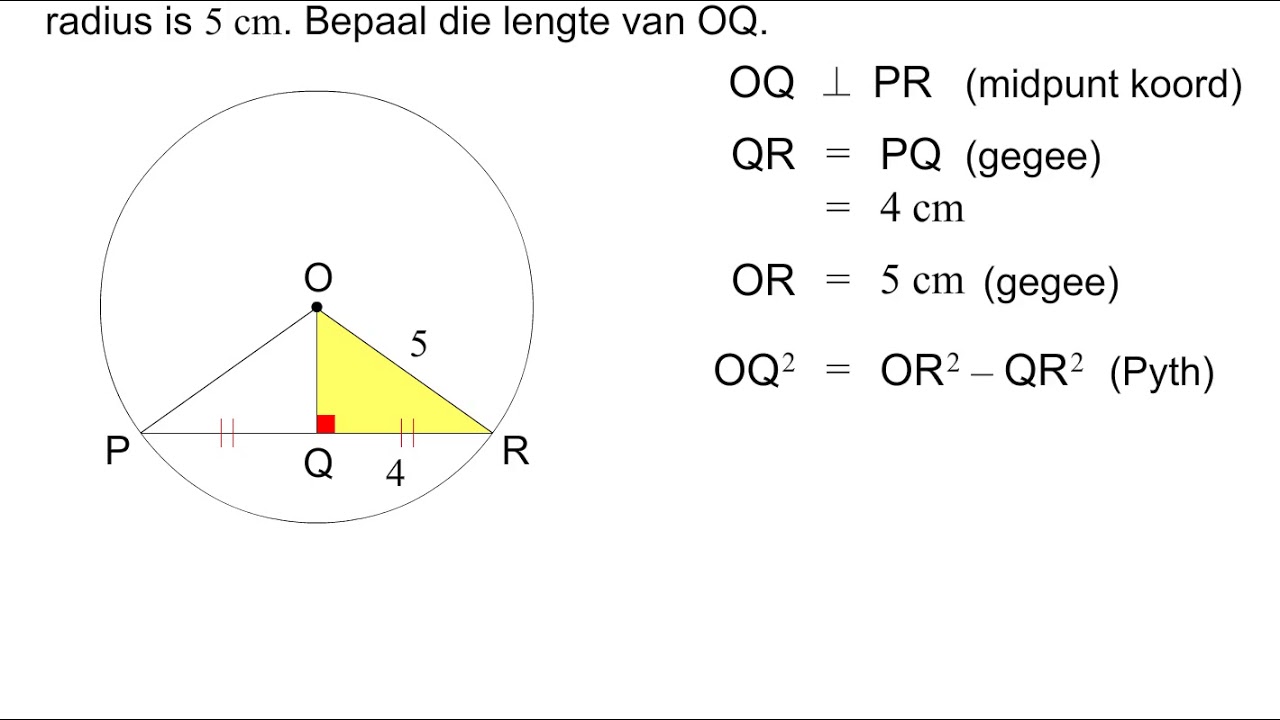
This instructional video explains circle basics—radius, diameter (d = 2r), chords—and key theorems: a perpendicular from the center to a chord bisects it, and chords equidistant from the center are congruent. It works through algebraic examples: setting 5x+3 = 7x−5 to find x = 4 and fg = 46, and solving a midpoint relation to get x = 6 and DE = 56. The lesson then applies the Pythagorean theorem to geometry problems: finding a circle’s radius from a 16-cm chord 6 cm from the center (r = 10), computing the center-to-chord distance with a 26-cm diameter (5 cm), and an inscribed 6×8 rectangle (r = 5).

Takeaways

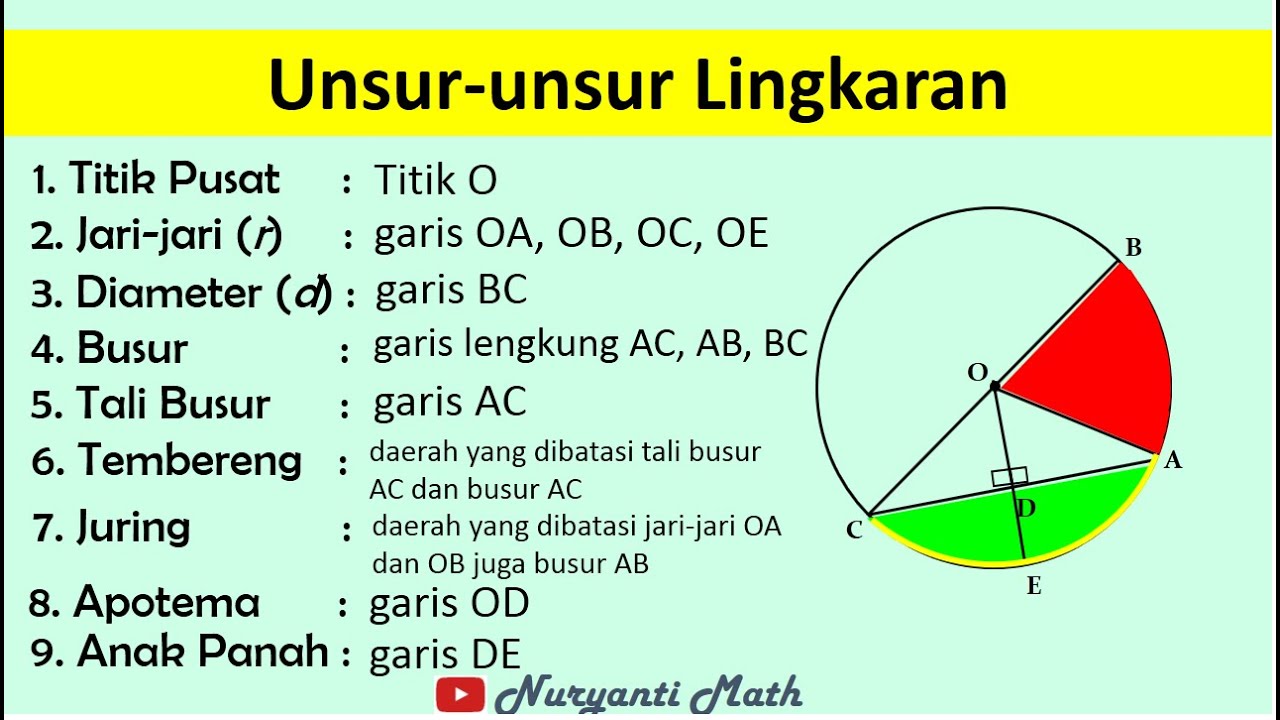
• 😀 The radius of a circle is the distance from the center to any point on the circle.
• 😀 The diameter of a circle is twice the length of the radius, and it passes through the center of the circle.
• 😀 A chord is a line segment connecting two points on the circle that does not necessarily pass through the center.
• 😀 If a segment from the center is perpendicular to a chord, it bisects the chord into two equal parts.
• 😀 When two chords are equidistant from the center of the circle, they are congruent (equal in length).
• 😀 If a segment from the center is perpendicular to a chord, the midpoint of the chord is the point where the segment intersects.
• 😀 The Pythagorean theorem can be used to calculate the radius of a circle when a right triangle is formed by the radius, half of the chord length, and the perpendicular distance from the center.
• 😀 If two chords are congruent, their distances from the center are also equal.
• 😀 The midpoint of a chord is where the perpendicular line from the center meets the chord, splitting the chord into two equal segments.
• 😀 When solving for missing lengths in circle-related problems, algebraic equations can be set up using known properties (e.g., setting two distances equal when they are congruent).

Q & A

What is the radius of a circle?

The radius of a circle is the distance from the center of the circle to any point on the circumference of the circle.

What is the relationship between the diameter and the radius of a circle?

The diameter of a circle is twice the length of the radius, or mathematically, D = 2r.

What is a chord in a circle?

A chord is a line segment that connects two points on the circle. It doesn't necessarily pass through the center of the circle.

What happens when a line from the center of a circle is perpendicular to a chord?

When a line from the center of the circle is perpendicular to a chord, it bisects the chord, meaning it divides the chord into two congruent parts.

How do we know if two chords in a circle are congruent?

Two chords in a circle are congruent if they are equidistant from the center of the circle. This means that the distances from the center to each chord are the same.

What does it mean if two segments drawn from the center of a circle are congruent?

If two segments drawn from the center of a circle are congruent, it means the corresponding chords are also congruent. This is because the distance from the center to each chord is the same.

How can we find the length of a chord using the Pythagorean theorem?

You can use the Pythagorean theorem to find the length of a chord by considering a right triangle formed by the radius of the circle, half the length of the chord, and the perpendicular distance from the center of the circle to the chord.

In the example with two congruent chords, how do we solve for the value of x when given expressions for the distances from the center?

To solve for x, set the two distance expressions from the center equal to each other, then solve the resulting equation algebraically. Once x is found, substitute it back into the expressions to find the lengths of the chords.

What is the method for finding the radius of a circle when given a rectangle inscribed in the circle?

To find the radius of a circle with an inscribed rectangle, use the Pythagorean theorem. The diagonal of the rectangle is the diameter of the circle, and half of this diagonal is the radius.

What is the relationship between the diameter and the radius when solving for the distance between the center and a chord?

The radius is half of the diameter. Once the radius is determined, you can use it in the Pythagorean theorem to solve for the distance between the center and the chord.