Delineamento em Blocos Casualizados (DBC) - Profª Camila Maida

Summary

This transcript covers a detailed explanation of randomized block design in experimental research. The speaker introduces key concepts such as repetition, randomization, and local control, emphasizing their importance in controlling variation within experiments. It explains how blocks are created to group experimental units with similar characteristics and how treatments are applied within these blocks. The statistical analysis of variance (ANOVA) for randomized block designs is also discussed, illustrating how to calculate degrees of freedom, sum of squares, and the F-test to determine the effectiveness of treatments. An example involving the testing of energy sources for broiler chickens is provided to highlight practical application.

Takeaways

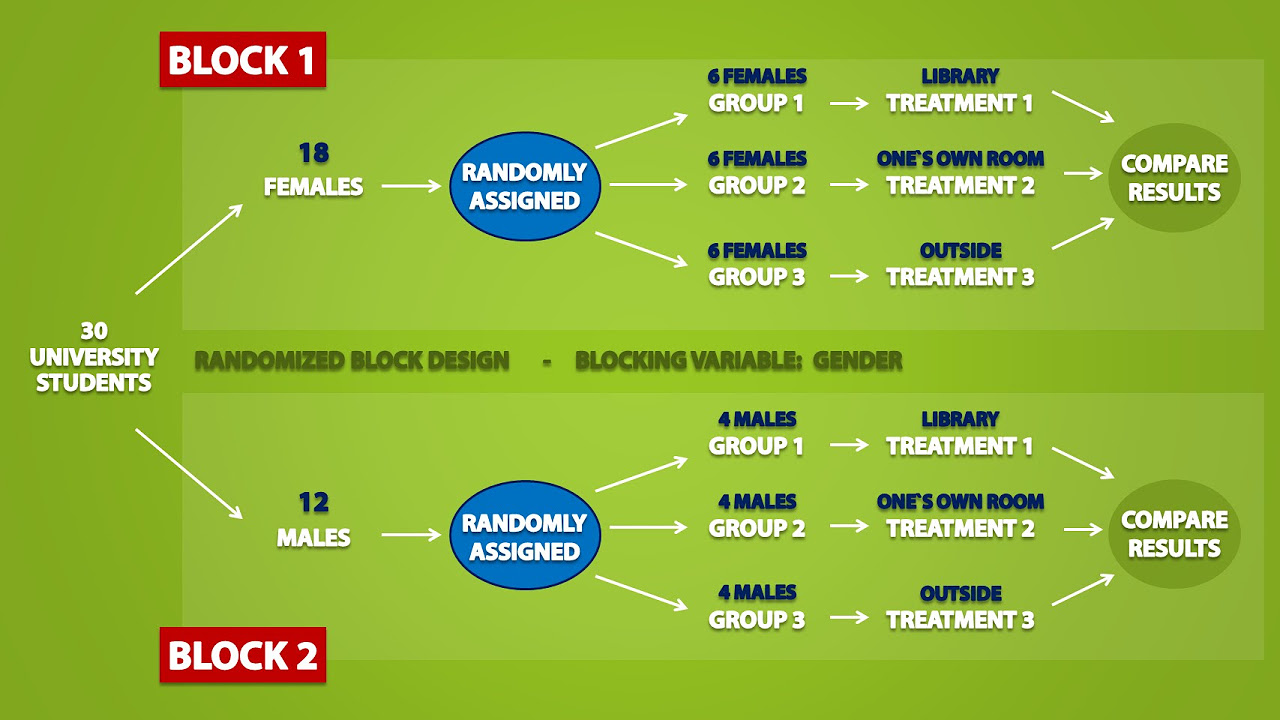
• 😀 Randomized Block Design (RBD) is a way to arrange treatments in experimental units by controlling known sources of variation.
• 😀 The three main experimental designs are: Completely Randomized Design (CRD), Randomized Block Design (RBD), and Latin Square Design.
• 😀 In Randomized Block Design, treatments are randomized within blocks, with the aim to control for local sources of variation.
• 😀 The three basic principles of experimentation in RBD are repetition, randomization, and local control.
• 😀 Local control in RBD is used to minimize variation between experimental units, for example by grouping animals with similar characteristics into blocks.
• 😀 The statistical model for RBD involves the general mean, treatment effect, block effect, and experimental error.
• 😀 In Analysis of Variance (ANOVA) for RBD, the total variation is decomposed into sums of squares for treatment, blocks, and residuals.
• 😀 Degrees of freedom in ANOVA are calculated for treatments, blocks, and residuals to determine the sources of variation in the data.
• 😀 The F-test is used to determine if treatments have statistically different effects, based on the ratio of treatment mean square to residual mean square.
• 😀 A practical example of RBD is testing the effect of energy sources on broiler chickens, where the block accounts for temperature differences between experimental units.
• 😀 The Tukey's test or other comparison tests are used after an F-test to identify which specific treatments have statistically different effects.

Q & A

What is the purpose of training in randomized block design?

Training in randomized block design is aimed at arranging treatments in experimental units. It helps in drawing treatments into these units in a structured way while controlling for specific sources of variation.

What are the three main types of experimental designs discussed in the transcript?

The three main types of experimental designs mentioned are the Completely Randomized Design, Randomized Block Design, and Latin Square Design.

What is the primary difference between the randomized block design and the Latin square design?

The primary difference is that in the randomized block design, treatments are drawn within blocks without local control. In contrast, the Latin square design controls randomization both horizontally and vertically within blocks.

What are the three basic principles of experimentation in the randomized block design?

The three basic principles are repetition, randomization, and local control.

How is local control used in randomized block design?

Local control in randomized block design is used to manage heterogeneity among experimental units. This heterogeneity could be due to factors like weight or age differences. By grouping units into subgroups (blocks), the design ensures that these differences are controlled during the experiment.

How is the statistical model of the randomized block design structured?

The statistical model of the randomized block design includes the general mean of the experiment, the effect of the treatment, the effect of the block, and experimental error as components that affect the response variable.

What is the role of analysis of variance (ANOVA) in randomized block design?

ANOVA helps decompose the total variation in the data into components like treatment, block, and residual variation. This allows the researcher to assess the significance of treatments and blocks in the experiment.

What does the F-test in ANOVA determine in randomized block design?

The F-test in ANOVA determines whether the treatments have statistically different effects. If the calculated F-value is greater than or equal to the tabled F-value, the null hypothesis is rejected, indicating that treatments have differing effects.

What is the significance of the block in the randomized block design example provided?

In the example, the block accounts for temperature differences between the lower and upper floors of a laboratory, where birds are housed. The difference in temperature is a known source of variation, and the block helps control for this effect in the experiment.

How is the sum of squares calculated in randomized block design?

The sum of squares is calculated by squaring all the observations and subtracting the correction value. The sum is then decomposed into treatment sum of squares, block sum of squares, and residual sum of squares. The calculations help quantify variation due to treatments, blocks, and error.