Persamaan Kuadrat • Part 4: Menyelesaikan Persamaan Kuadrat dengan Rumus abc
Summary
TLDRIn this video, viewers are introduced to solving quadratic equations using the quadratic formula (ABC formula). The host explains how to derive the formula through the method of completing the square and simplifies its application. The video walks through step-by-step solutions to various quadratic equations, showing both the process and the importance of understanding the components (a, b, c). The host also compares this method with factorization, recommending the quadratic formula for consistency in solving more complex problems. Tips for choosing the right method are provided, along with practical examples.
Takeaways
- 😀 The video discusses solving quadratic equations using the quadratic formula (abc formula).
- 😀 The quadratic formula is X1,2 = (-b ± √(b² - 4ac)) / 2a.
- 😀 X1 and X2 represent the two possible solutions of a quadratic equation.
- 😀 The process of solving with the abc formula involves identifying the values of a, b, and c in the quadratic equation.
- 😀 The formula gives two results due to the ± sign, representing the positive and negative solutions.
- 😀 The video emphasizes understanding the origin of the quadratic formula, not just memorizing it.
- 😀 The quadratic formula is derived through the method of completing the square, a previous topic discussed in the series.
- 😀 The discriminant (D) is the term b² - 4ac, and it is often abbreviated as D in the formula.
- 😀 Examples are provided for solving quadratic equations, demonstrating step-by-step how to apply the quadratic formula.
- 😀 The video compares three methods of solving quadratic equations: factoring, completing the square, and using the quadratic formula.
- 😀 The video suggests using the quadratic formula when factoring is difficult or inefficient, especially when the equation has large numbers or irrational roots.
Q & A
What is the quadratic formula, and how is it used?
-The quadratic formula is X₁,₂ = -b ± √(b² - 4ac) / 2a. It is used to solve quadratic equations of the form ax² + bx + c = 0 by plugging in the values of a, b, and c into the formula to find the solutions, X₁ and X₂.
What do X₁ and X₂ represent in the quadratic formula?
-X₁ and X₂ represent the two possible solutions (or roots) of the quadratic equation. These are the values of x that satisfy the equation ax² + bx + c = 0.
How are the two results (X₁ and X₂) derived from the quadratic formula?
-The two results are derived by separating the plus and minus signs in the quadratic formula. One solution uses the positive sign (+), and the other uses the negative sign (-), which results in two different values for X₁ and X₂.
How is the discriminant (D) defined in the context of the quadratic formula?
-The discriminant, denoted as D, is the expression inside the square root of the quadratic formula, b² - 4ac. It helps determine the nature of the solutions: if D is positive, there are two real solutions; if D is zero, there is one real solution; and if D is negative, the solutions are complex.
What is the process for deriving the quadratic formula using the method of completing the square?
-To derive the quadratic formula, we start with the general quadratic equation ax² + bx + c = 0. By moving the constant term to the other side and dividing by a to make the coefficient of x² equal to 1, we then complete the square on the left side. After simplifying, we end up with the quadratic formula, X₁,₂ = -b ± √(b² - 4ac) / 2a.
Why is the quadratic formula considered more convenient than completing the square?
-The quadratic formula is more convenient because it provides a direct and simple way to solve quadratic equations without the need to manipulate the equation further, unlike completing the square, which involves more steps and calculations.
Can all quadratic equations be factored easily?
-No, not all quadratic equations can be factored easily. Some equations might have large coefficients or result in complex solutions, making factoring impractical or impossible. In such cases, the quadratic formula is a more reliable method.
What is the recommended strategy for solving quadratic equations when the method is not specified?
-If the method is not specified, it's recommended to first try factoring the equation. If factoring is difficult or does not work, then use the quadratic formula. The quadratic formula is guaranteed to give a solution, regardless of the equation's complexity.
Why is completing the square not always recommended for solving quadratic equations?
-Completing the square is not always recommended because it is more complex and time-consuming compared to other methods like factoring or using the quadratic formula. It may also be less efficient for beginners, especially when dealing with larger or more complicated equations.
In the example problem 2x² + 3x - 2 = 0, how are the values of X₁ and X₂ found using the quadratic formula?
-For the equation 2x² + 3x - 2 = 0, the coefficients are a = 2, b = 3, and c = -2. Substituting these values into the quadratic formula results in X₁ = 1/2 and X₂ = -2.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Persamaan Kuadrat Kelas 10 Kurikulum Merdeka
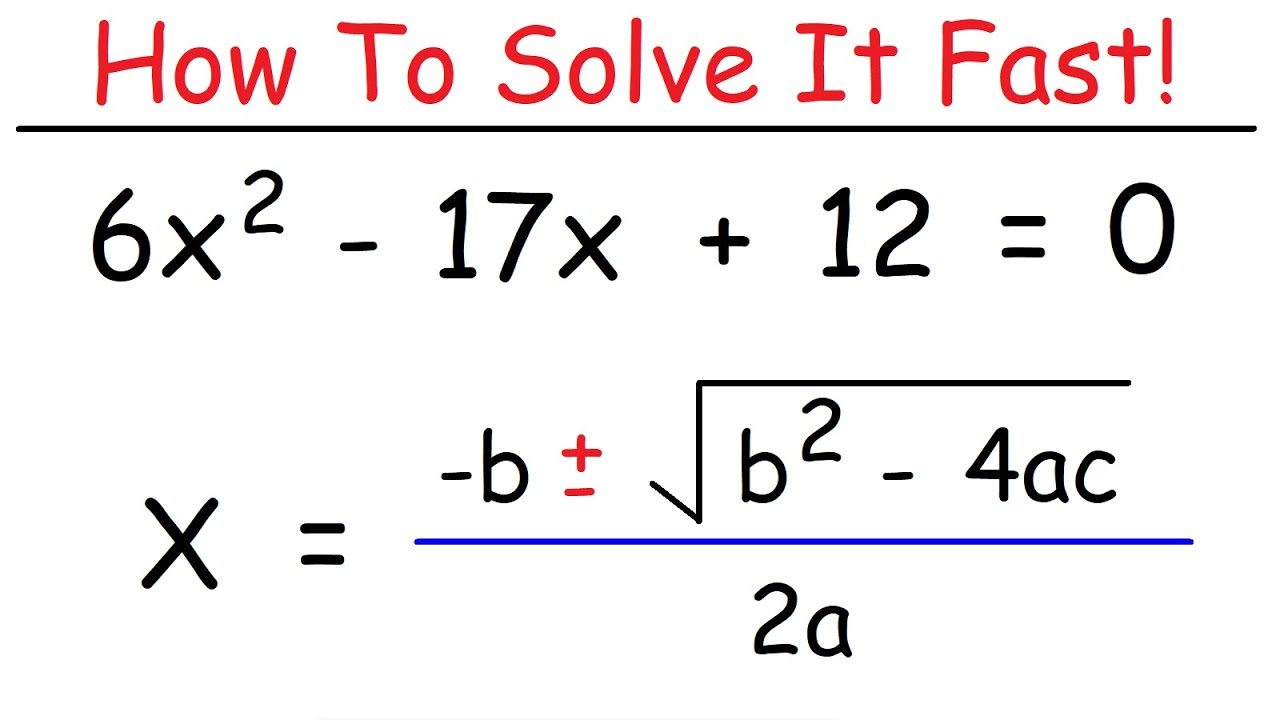
How To Solve Quadratic Equations Using The Quadratic Formula

Solving Equations Transformable into Quadratic Equations

Solving Quadratic Equation Using Quadratic Formula

Materi Kuliah Model Simulasi: Pembangkit Random Variate Kontinu

Bilangan Kompleks • Part 2: Bilangan Imajiner
5.0 / 5 (0 votes)
