Complex Numbers : Modulus and Argument | ExamSolutions
Summary
TLDR本视频介绍了复数的模和辐角概念。首先,复数的模是指从原点到复数在复平面上的点的距离,可以通过勾股定理计算。其次,复数的辐角是复数与实数轴之间的角度,通常使用弧度表示。视频通过多个例题,讲解了如何通过绘制三角形、使用反正切函数来计算复数的模和辐角,并强调了绘制图形的重要性,以帮助避免错误。
Takeaways
- 😀 复数的模是复数到原点的距离,使用毕达哥拉斯定理计算,即 |Z| = √(a² + b²)。
- 😀 复数的模常常表示为 |Z| 或 mod Z,所有形式都指代复数的模,计算公式一致。
- 😀 复数的辩论是复数与实轴之间的夹角,记作 Arg(Z),范围为 -π 到 π 弧度。
- 😀 使用弧度来测量角度,而不是度数,通常情况下,角度Θ是通过反正切函数(arctan)计算得到的。
- 😀 角度计算时,避免直接使用复数的虚部和实部的符号,正确的做法是考虑三角形的正值。
- 😀 复数的 argument 通过构建直角三角形来计算,其中使用正对边除以邻边的比值,得到 α。
- 😀 要准确计算 argument,要画出复数图像,标出急角度 α,确保计算不出错。
- 😀 通过反正切函数(arctan)可以得到急角度 α,之后可通过 π - α 计算复数的辩论角度。
- 😀 若复数位于第三象限或第四象限,辩论角度将是负数,需要通过调整角度的计算来考虑象限。
- 😀 在实际应用中,复数的模和辩论角度的计算常常结合习题,以帮助学生熟悉和掌握这些概念。
Q & A
什么是复数的模?
-复数的模指的是复数在复平面上表示的点到原点的距离。它可以通过勾股定理计算,公式为 |Z| = √(a² + b²),其中a和b分别是复数Z = a + bi的实部和虚部。
如何计算复数的模?
-复数的模可以通过勾股定理来计算。设复数为Z = a + bi,其中a为实部,b为虚部。模的计算公式为 |Z| = √(a² + b²)。
复数的 argument 是什么?
-复数的 argument(辐角)是复数在复平面上与正实轴之间的角度,通常记作θ。这个角度的范围是 -π ≤ θ ≤ π,单位是弧度。
如何计算复数的 argument?
-复数的 argument 可以通过计算复数与正实轴之间的夹角来求得。首先计算复数的相对角度(acute angle),然后根据所处的象限调整角度的符号,使用反正切函数(arctan)求解该角度。
在计算 argument 时需要注意什么?
-计算复数的 argument 时,需要注意所处象限的符号。角度通常在 -π 到 π 之间,如果复数位于第三象限或第四象限,角度会是负值。必须根据实际象限调整角度的值。
什么是反正切(arctan)函数在计算 argument 中的应用?
-反正切(arctan)函数用于计算复数的相对角度(acute angle)。在计算 argument 时,使用反正切函数求出该角度,公式为 arctan(|b| / |a|),其中a和b分别是复数的实部和虚部的绝对值。
复数 ARG 的符号如何影响最终结果?
-复数的 ARG(辐角)的符号依赖于复数所在的象限。如果复数位于第一或第二象限,角度为正;如果复数位于第三或第四象限,角度为负。根据这些象限的规则调整角度的符号。
在复数的模和 argument 计算中,如何处理负数?
-在计算复数的模时,只关注实部和虚部的绝对值,因此不管它们是正是负。对于 argument 的计算,负的实部或虚部会影响角度的符号,根据所在象限决定角度是否为负。
计算复数模时,如何处理虚部或实部为负的情况?
-计算复数模时,无论实部或虚部是否为负,都需要取它们的绝对值来计算模。因此,复数Z = -3 - 4i 的模是 √((-3)² + (-4)²) = 5。
如何通过示意图帮助计算复数的模和 argument?
-通过在复平面上绘制复数的示意图,可以更清楚地了解复数的模和 argument。画出从原点到复数的线段,计算该线段的长度得到模;通过计算复数与正实轴的夹角来得到 argument,注意根据象限调整角度的符号。
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

What are Transformer Models and how do they work?

Computer Vision: Crash Course Computer Science #35
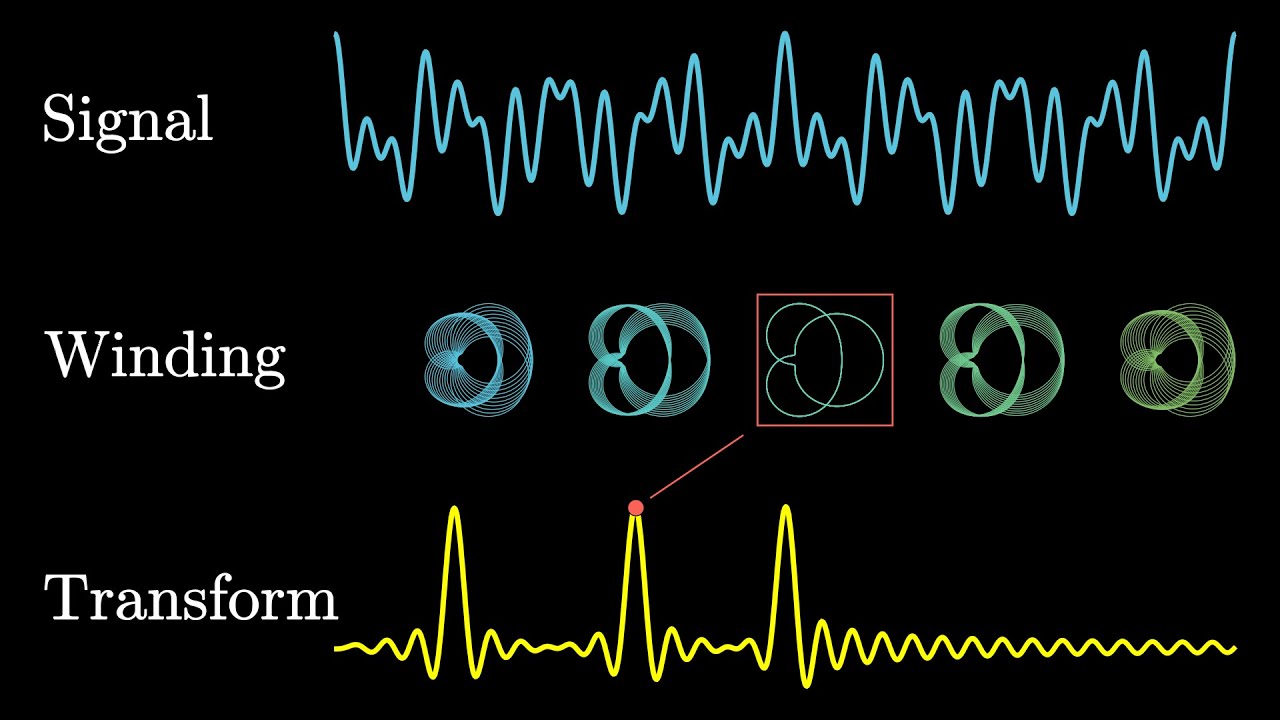
But what is the Fourier Transform? A visual introduction.

Hibridación del carbono

Produkt-, Quotienten- und Kettenregel

LangGraph Crash Course with code examples

[ e - Learning ] Power Factor Correction (PFC) - Basics of Switching Power Supplies (4)
5.0 / 5 (0 votes)
