Illustrate Polynomial Functions | Second Quarter | Grade 10 MELC
Summary
TLDRThis video explains the fundamentals of polynomial functions, covering their form, components, and classification. A polynomial function is expressed as a sum of terms with non-negative integer exponents. Key elements include the degree, leading term, leading coefficient, and constant term. The video provides examples of different types of polynomial functions, including cubic, quadratic, and linear functions, while also clarifying what does not qualify as a polynomial (e.g., negative or fractional exponents, variables in the denominator, or under a radical sign). The video concludes by identifying valid and invalid polynomial functions from a set of expressions.
Takeaways
- 😀 A polynomial function is an expression of the form p(x) = a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x + a_0, where the exponents are non-negative integers and the leading coefficient a_n is non-zero.
- 😀 The degree of a polynomial function is the highest exponent of the variable x.
- 😀 The leading term of a polynomial is the term with the highest exponent, and its coefficient is called the leading coefficient.
- 😀 The constant term in a polynomial is the term without a variable (a_0).
- 😀 A polynomial function is considered to be in standard form when its terms are written in decreasing powers of x.
- 😀 A polynomial function can be written in any order, but the standard form arranges terms in decreasing powers of x.
- 😀 Example of a cubic polynomial: p(x) = 2x^3 + x^2 - 18x + 7, with degree 3, leading term 2x^3, and constant term 7.
- 😀 Example of a quadratic polynomial: f(x) = x^2 + 6x - 10, with degree 2, leading term x^2, and constant term -10.
- 😀 Example of a linear polynomial: g(x) = 6x + 5, with degree 1, leading term 6x, and constant term 5.
- 😀 A function is not a polynomial if the variable appears in the denominator (e.g., f(x) = 6/5x), has a negative exponent (e.g., p(x) = 5x^{-2}), or has a fractional exponent (e.g., h(x) = x^{1/3}).
- 😀 Functions with variables under a radical sign, such as g(x) = √(5x), are not polynomials.
- 😀 Identifying polynomial functions involves checking that the terms of the expression have non-negative integer exponents and that no terms involve fractions or radicals.
Q & A
What is a polynomial function?
-A polynomial function is a function of the form p(x) = a_n * x^n + a_(n-1) * x^(n-1) + ... + a_1 * x + a_0, where a_n, a_(n-1), ..., a_0 are real numbers, and a_n is not equal to 0. The degree of the polynomial is n, and a_n is the leading coefficient.
What is the degree of a polynomial function?
-The degree of a polynomial function is the highest power of the variable x in the function. For example, in p(x) = 2x^3 + x^2 - 18x + 7, the degree is 3, making it a cubic function.
What is the leading term of a polynomial function?
-The leading term of a polynomial function is the term with the highest power of x. For instance, in p(x) = 2x^3 + x^2 - 18x + 7, the leading term is 2x^3.
What is the constant term in a polynomial?
-The constant term in a polynomial is the term that does not contain the variable x. In the example p(x) = 2x^3 + x^2 - 18x + 7, the constant term is 7.
How do you determine the leading coefficient of a polynomial function?
-The leading coefficient of a polynomial is the coefficient of the term with the highest power of x. For example, in p(x) = 2x^3 + x^2 - 18x + 7, the leading coefficient is 2.
What is the difference between a polynomial and a non-polynomial function?
-A polynomial function has terms that are powers of x with non-negative integer exponents, and the variable is not in the denominator or under a radical. Non-polynomial functions may involve negative exponents, fractional exponents, or the variable in the denominator or under a radical sign.
Can a function with a variable in the denominator be a polynomial?
-No, a function with a variable in the denominator is not a polynomial. For example, f(x) = 6 / 5x is not a polynomial because the variable x is in the denominator.
Why is x^(-2) not considered part of a polynomial function?
-x^(-2) is not part of a polynomial function because polynomials can only have non-negative integer exponents. A negative exponent, like x^(-2), disqualifies the expression from being a polynomial.
What does it mean when a polynomial is written in standard form?
-A polynomial is in standard form when its terms are ordered in decreasing powers of x, with the highest degree term first. For example, the standard form of p(x) = 2x^3 + x^2 - 18x + 7 has terms in descending order of powers of x.
What is an example of a polynomial function of degree 2?
-An example of a polynomial function of degree 2 is f(x) = x^2 + 6x - 10, which is a quadratic function. The degree is 2 because the highest power of x is x^2.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
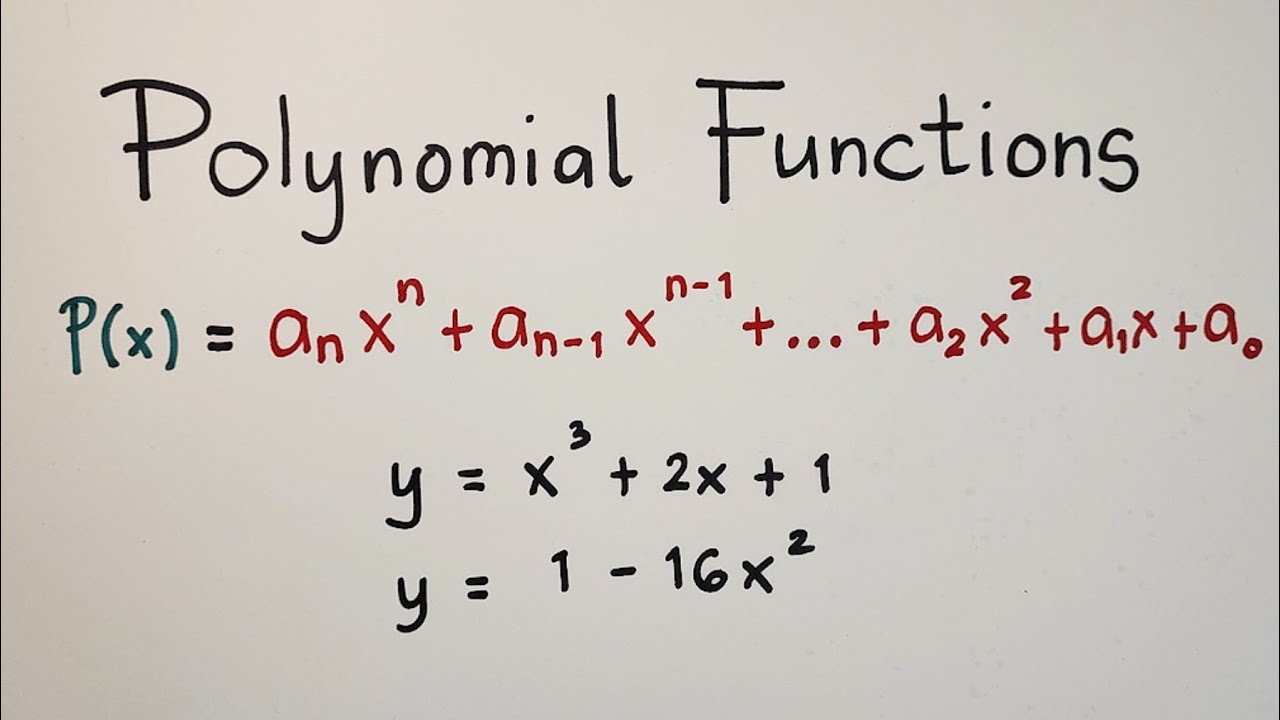
Polynomial Functions - Polynomial Function or NOT? Grade 10 Math Second Quarter

ILLUSTRATING POLYNOMIAL FUNCTIONS || GRADE 10 MATHEMATICS Q2

Ganzrationale Funktionen (Polynomfunktionen) - Einführung / Grundlagen

Polynomial Functions | Don't Memorise

POLINÔMIOS #01 | DEFINIÇÃO FORMA REDUZIDA E GRAU DE UM POLINÔMIO | \Prof. Gis/

Polinomial (Bagian 5) - Cara Menentukan Akar-akar Persamaan Polinomial
5.0 / 5 (0 votes)
