Área de una región plana utilizando sumatorias
Summary
TLDREn este video se explica cómo calcular el área bajo una curva utilizando sumatorias. Se empieza con una función lineal simple y se calcula el área de un triángulo rectángulo con la fórmula tradicional de base por altura entre dos. Luego, se introduce un método más general utilizando sumatorias y rectángulos, mostrando cómo al hacer más pequeños los rectángulos, el cálculo del área se vuelve más preciso. Finalmente, se presenta el concepto del límite cuando los rectángulos son infinitamente pequeños, demostrando que este enfoque es útil para funciones más complejas.
Takeaways
- 📐 El área bajo la curva se puede calcular utilizando sumatorias de rectángulos.
- 📏 Se inicia con una función lineal f(x) = x y se calcula el área del triángulo formado entre la recta y el eje x desde x = 0 hasta x = 3.
- 📊 El área del triángulo se calcula usando la fórmula base por altura entre 2, resultando en 4.5.
- 🔢 Para áreas bajo curvas más complejas, se dividen en rectángulos de base delta x y altura f(x).
- 🧮 Se utiliza la notación sigma para sumar el área de todos los rectángulos.
- 📉 Rectángulos circunscritos sobresalen del área de interés, mientras que los inscritos están dentro.
- 📏 Cuantos más rectángulos con delta x más pequeño, más preciso será el cálculo del área.
- 📐 Al hacer delta x infinitamente pequeño, el cálculo se aproxima al área real mediante un límite.
- 📝 El límite se calcula como una sumatoria infinita, sustituyendo valores y simplificando.
- ✅ Finalmente, el área obtenida usando límites coincide con el área calculada con la fórmula del triángulo, resultando en 4.5.
Q & A
¿Qué es el área bajo la curva?
-El área bajo la curva es la región entre una función y el eje x. En el caso de una función lineal, como la función f(x) = x, esta área se puede calcular fácilmente utilizando la fórmula de un triángulo, pero para funciones más complejas se requiere un método más general.
¿Cómo se calcula el área de un triángulo en este contexto?
-El área de un triángulo se calcula usando la fórmula base por altura dividida entre dos. En este caso, la base es el valor en el eje x (de 0 a 3) y la altura es el valor de la función en x = 3. El área es 4.5.
¿Por qué se usan rectángulos para aproximar el área bajo la curva?
-Se usan rectángulos porque permiten dividir el área en pequeñas secciones, lo que facilita la suma de áreas más simples para aproximar la región total bajo la curva, especialmente cuando la función es compleja.
¿Qué es el valor de delta x y cómo se calcula?
-Delta x es el ancho de cada rectángulo y se calcula tomando el valor máximo del eje x menos el valor mínimo, dividido entre la cantidad de rectángulos. En este caso, delta x es igual a 3/n.
¿Qué diferencia hay entre rectángulos circunscritos e inscritos?
-Los rectángulos circunscritos sobresalen del área de interés, mientras que los rectángulos inscritos están contenidos dentro del área bajo la curva.
¿Qué sucede cuando se utilizan muchos rectángulos para aproximar el área?
-Cuando se usan más rectángulos y delta x se hace más pequeño, la aproximación del área se vuelve más precisa, hasta el punto en que el error se reduce significativamente si se utilizan infinitos rectángulos pequeños.
¿Cómo se puede calcular el área bajo una curva cuando los rectángulos son infinitamente pequeños?
-El área se puede calcular utilizando el límite cuando el número de rectángulos tiende a infinito, sumando el producto de la función evaluada en cada punto por delta x, lo que nos da el área exacta.
¿Cómo se aplica la notación sigma en el cálculo del área?
-La notación sigma se usa para representar la sumatoria de las áreas de los rectángulos. En este caso, se usa para sumar el producto de f(xi) por delta x desde i = 1 hasta n, donde n es el número de rectángulos.
¿Cuál es el papel del límite en el cálculo del área bajo la curva?
-El límite es esencial porque nos permite aproximar el área exacta bajo la curva cuando el número de rectángulos tiende a infinito, lo que significa que los rectángulos son infinitamente pequeños.
¿Cuál es la relación entre este método y el cálculo del área de un triángulo simple?
-Para funciones simples como f(x) = x, ambos métodos (el de triángulo y el de sumatoria) llegan al mismo resultado: un área de 4.5. Sin embargo, el método de la sumatoria es útil para curvas más complejas donde la fórmula del triángulo no se aplica.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Sumatorias

Área bajo la curva por Extremos Derechos

Método: rectángulos CIRCUNSCRITOS | Área bajo la curva | Cálculo Integral

Cálculo Integral 01:Área bajo una curva. Area under a curve
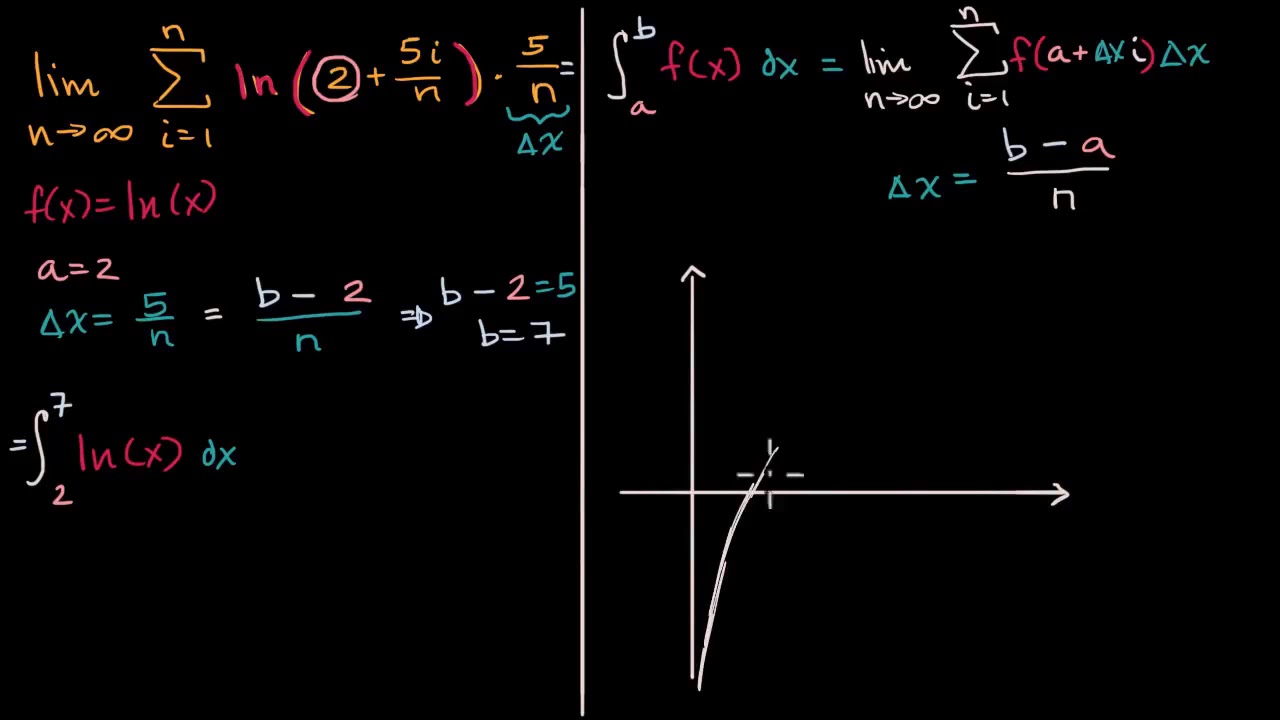
Escribir el límite de una suma de Riemann como una integral definida | Khan Academy en Español

Reescribir una integral definida como el límite de una suma de Riemann | Khan Academy en Español
5.0 / 5 (0 votes)
