Eksempel 1
Summary
TLDRThe script explores the concept of decision-making under uncertainty using a lottery scenario involving Jens, who has a utility function U(x) = √x. Jens is given a choice to participate in a lottery with a 50% chance of winning 125 DKK or losing 100 DKK. The script calculates the expected value and expected utility of the lottery, determining Jens' willingness to participate based on the difference between the expected value and his security equivalent. The concept of risk premium is introduced, illustrating Jens' aversion to risk and how it influences his decision.
Takeaways
- 🎰 The script discusses a lottery scenario involving a person named Jens, who has a 50% chance of winning 125 DKK and a 50% chance of losing 100 DKK.
- 💼 Jens starts with 100 DKK, which is used as a baseline to calculate potential outcomes of the lottery.
- 📈 Jens has a utility function, U(x) = √x, which translates monetary amounts into utility or satisfaction.
- 🔢 The expected utility of the lottery is calculated by multiplying the utility of each outcome by its probability and summing them up, resulting in 7.5.
- 📉 The expected monetary value of the lottery is 112.5 DKK, which is the average outcome if the lottery were played many times.
- 💡 The script introduces the concept of 'security equivalent', which is the amount of money that provides the same utility as the lottery, calculated to be 56.25 DKK for Jens.
- 🚫 Jens would not prefer to participate in the lottery as his expected utility after participating is less than his current utility.
- ✅ The 'security equivalent' is the amount Jens would be indifferent to receiving instead of participating in the lottery.
- 💰 The 'risk premium' is the difference between the expected value of the lottery and the security equivalent, calculated as 56.25 DKK in this case.
- 📊 The script uses a graphical representation to illustrate Jens's utility function and how it compares to the expected utility of the lottery and the security equivalent.
Q & A
What is the lottery game Jens is participating in?
-Jens is participating in a lottery where there are two possible outcomes: a 50% chance of winning 125 DKK and a 50% chance of losing 100 DKK.
What is Jens' initial amount of money before participating in the lottery?
-Jens initially has 100 DKK in his pocket.
What is the utility function Jens uses to evaluate monetary outcomes?
-Jens uses a utility function U(x) = √x, where x represents the amount of money in DKK.
What is the expected utility of Jens before participating in the lottery?
-Before participating in the lottery, Jens' expected utility is 10, which is calculated as the square root of his initial 100 DKK.
What are the possible utility outcomes after Jens participates in the lottery?
-After participating in the lottery, Jens could either have a utility of 15 (if he wins 225 DKK) or 0 (if he loses and has 0 DKK).
What is Jens' expected utility after participating in the lottery?
-Jens' expected utility after participating in the lottery is 7.5, calculated by taking the weighted average of the utility outcomes (0.5 * 15 + 0.5 * 0).
Why might Jens not want to participate in the lottery?
-Jens might not want to participate in the lottery because his expected utility after participating (7.5) is less than his current utility (10), indicating a decrease in expected satisfaction.
What is the concept of 'security equivalent' in the context of Jens' decision?
-The security equivalent is the amount of money that would provide Jens with the same utility as his expected utility after participating in the lottery. In this case, it is 56.25 DKK.
How is the 'risk premium' calculated in Jens' lottery scenario?
-The risk premium is calculated as the difference between the expected value of the lottery (112.5 DKK) and the security equivalent (56.25 DKK), which in this case is also 56.25 DKK.
What does the risk premium represent in Jens' decision-making?
-The risk premium represents the amount Jens would be willing to pay to avoid the risk of participating in the lottery, indicating his risk aversion.
How does the concept of utility function help in understanding Jens' preference for risk?
-The utility function helps in understanding Jens' preference for risk by quantifying his satisfaction from different monetary outcomes. A concave utility function, like Jens' √x, indicates risk aversion, as he prefers a sure amount of money to a gamble with the same expected value.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
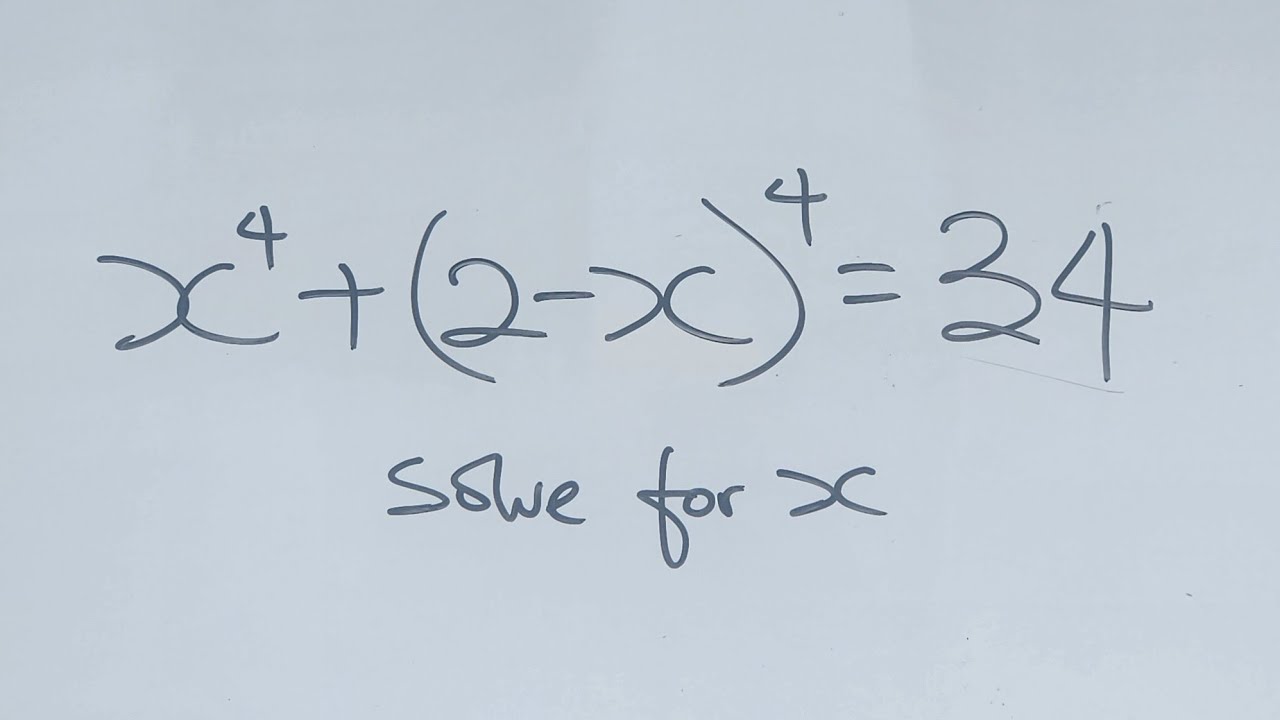
Maths Olympiad Question | A nice algebraic equation | You should know this trick!

Using Math to Find When Your Dad is Coming Back with the Milk
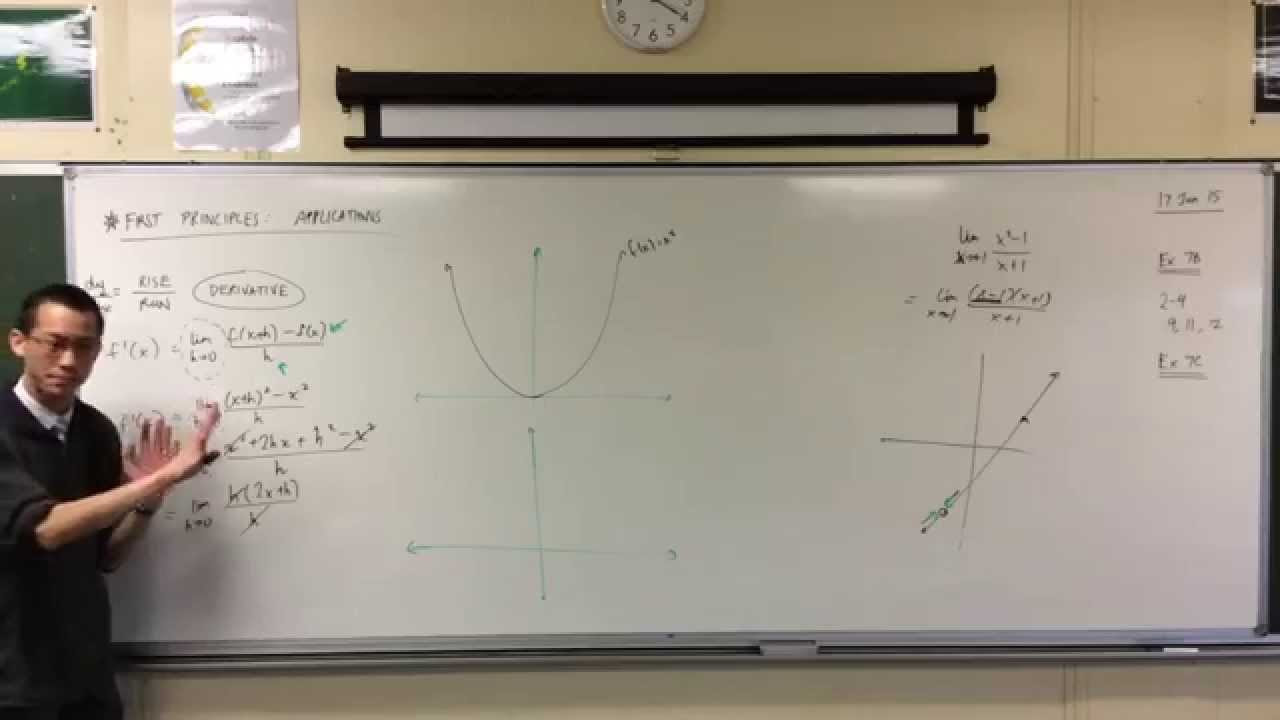
Applying First Principles to x² (1 of 2: Finding the Derivative)

Calculus - The limit of a function

Evaluating Functions - Basic Introduction | Algebra

Partial Differential Equations|Solving first Order PDE|Clairaut's Form|Solve z= px + qy + p^2+pq+q^2
5.0 / 5 (0 votes)
