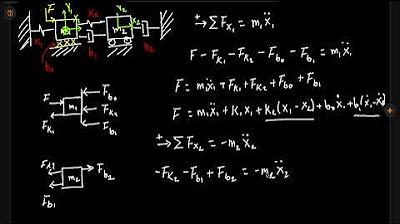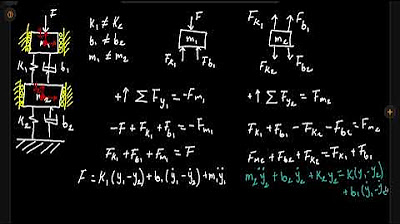Sistema de suspensión con multiples elementos de fricción
Summary
TLDREl vídeo explica un modelo matemático para un sistema con múltiples elementos de fricción y dos masas conectadas por resortes. Se definen fuerzas de fricción y una fuerza externa aplicada a una masa. Se establece un análisis unidimensional y se crean diagramas de cuerpo libre para ambas masas. Se derivan ecuaciones diferenciales que describen la dinámica del sistema, considerando la interacción entre las masas y los efectos de los resortes y amortiguadores.
Takeaways
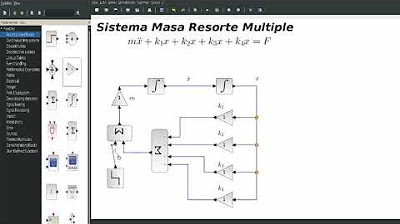
- 📊 El vídeo presenta un modelo matemático de un sistema con múltiples elementos de fricción y dos masas interconectadas por un resorte.
- 🧱 Se definen los elementos de fricción y se nombran los resortes y amortiguadores que interconectan las masas.
- 💨 Se asume la existencia de una fuerza externa aplicada a la masa 2 que causa la dinámica del sistema, y el análisis se realiza en un solo eje unidimensional.
- 🗺️ Se establecen los referenciales para el análisis del movimiento y se elige que la dirección hacia la izquierda sea positiva.
- 📐 Se generan los diagramas de cuerpo libre para las masas m1 y m2, indicando todas las fuerzas y fricciones actuando sobre cada masa.
- ⚖️ Para m2, las fuerzas de oposición incluyen fricciones, resortes, y amortiguadores que se colocan en el lado opuesto de la fuerza de excitación.
- 📝 Se plantean las ecuaciones diferenciales que describen la dinámica del sistema, comenzando con una sumatoria de fuerzas en los referenciales establecidos.
- 🔄 La ecuación de la masa 2 se simplifica a través de la factorización, obteniendo términos de posición, velocidad y amortiguamiento.
- 🔢 Se realiza un procedimiento similar para m1, considerando las fuerzas de los resortes y amortiguadores y obteniendo una ecuación diferencial.
- 🔗 Las ecuaciones resultantes están interconectadas a través de la fuerza generada por el resorte k2, que afecta a ambas masas.
Q & A
¿Qué elementos principales componen el sistema descrito en el vídeo?
-El sistema consta de dos masas interconectadas por un resorte, con fricción en la parte superior e inferior, y una fuerza externa aplicada a la masa 2.
¿Cuál es el objetivo del modelo matemático presentado?
-El objetivo es encontrar las ecuaciones matemáticas que describen el movimiento de un sistema con fricción y masas interconectadas, considerando una fuerza externa aplicada.
¿En qué dirección se considera que ocurre el movimiento del sistema?
-El movimiento se considera unidimensional, ocurriendo únicamente en un eje horizontal.
¿Cómo se describen las fuerzas de fricción en el sistema?
-Las fuerzas de fricción son descritas como elementos de oposición que se oponen al movimiento tanto de las masas como de los amortiguadores.
¿Qué fuerzas actúan sobre la masa 2?
-La masa 2 experimenta una fuerza de excitación hacia la derecha, la oposición del resorte k2 y k3, el amortiguador d2, y las fuerzas de fricción d5 y d6, todas actuando en diferentes direcciones.
¿Cómo se genera el diagrama de cuerpo libre para la masa 1?
-El diagrama de cuerpo libre para la masa 1 incluye la interacción indirecta con la fuerza externa a través del resorte k2, la oposición de los resortes k1 y k3, y la resistencia de los amortiguadores d1 y d4.
¿Qué se describe con las ecuaciones diferenciales obtenidas?
-Las ecuaciones diferenciales describen la dinámica del movimiento de las masas 1 y 2, tomando en cuenta las fuerzas externas, los resortes, los amortiguadores y las fricciones.
¿Qué rol juega el resorte k2 en la interacción entre las dos masas?
-El resorte k2 genera una fuerza que conecta las dos masas, afectando sus movimientos y siendo un elemento clave en la interacción entre ambas.
¿Cómo se simplifican las ecuaciones de movimiento para mejorar su claridad?
-Las ecuaciones se simplifican mediante factorización de términos comunes, agrupando elementos relacionados con la velocidad y la posición de las masas.
¿Qué suposiciones se hacen sobre la naturaleza de la fuerza externa aplicada?
-Se considera que la fuerza externa puede ser de tipo escalón, rampa, impulso, o una combinación de todas, y su naturaleza no se define completamente en el vídeo.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тариф5.0 / 5 (0 votes)