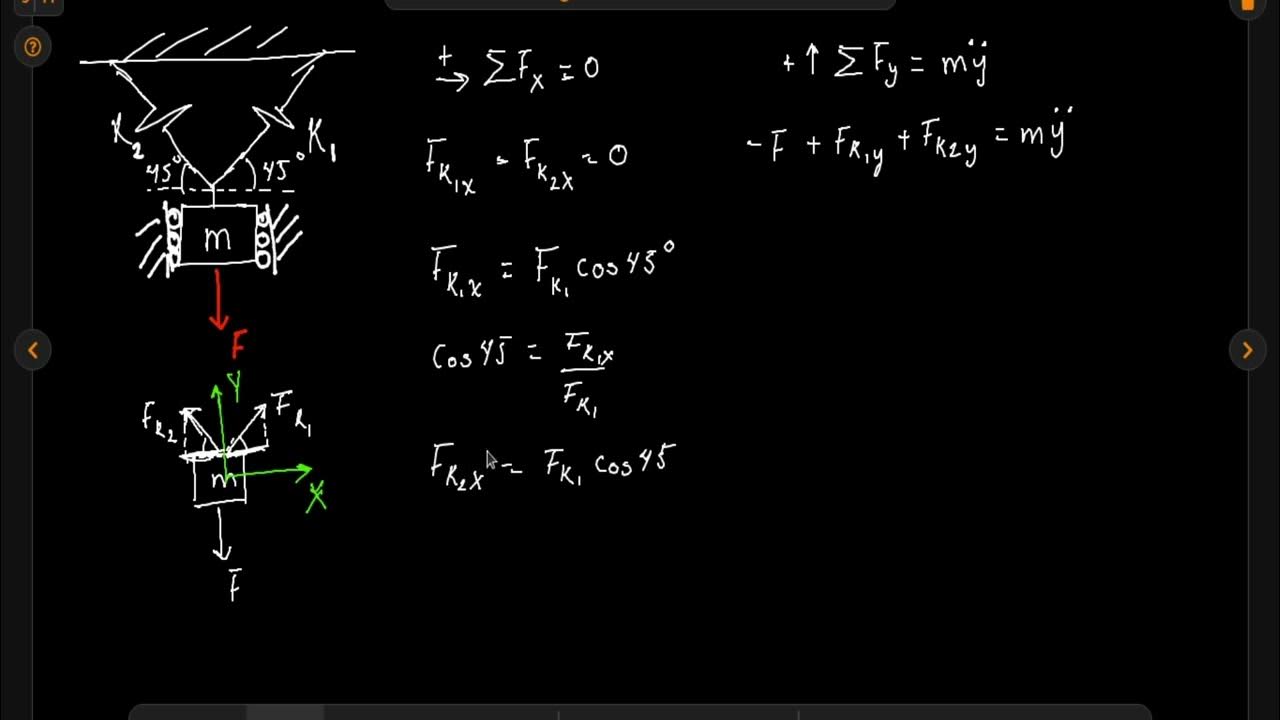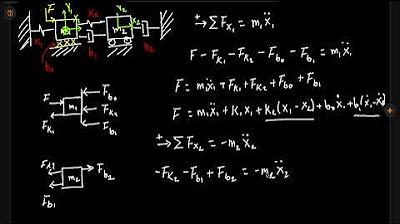Sistema Masa Resorte Multiple
Summary
TLDREn este vídeo se presenta un modelo matemático para un sistema de masa y resortes, donde cuatro resortes están dispuestos en pares a ambos lados de la masa. Se analiza la dinámica del sistema bajo la acción de una fuerza externa, sin considerar la fricción. Se establece un marco de referencia centrado en la masa, con ejes definidos hacia la derecha (eje x) y hacia abajo (eje y). Se realiza un análisis de fuerzas y se plantea una ecuación diferencial de segundo orden para describir el movimiento, donde la fuerza de cada resorte es proporcional a su deformación. La solución sugiere una oposición cuadrupla de los resortes a la fuerza externa, generando una ecuación que puede tener múltiples soluciones dependiendo de las constantes de los resortes.
Takeaways
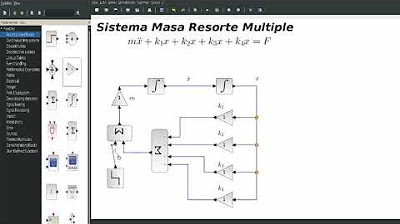
- 🔍 Se presenta un modelo matemático para un sistema de masa y resorte, donde se asume la existencia de cuatro resortes.
- 🌐 Se establece un marco de referencia centrado en la masa, con los ejes direccionados hacia la derecha (eje x) y hacia abajo (eje y).
- 🔄 Se considera una fuerza externa que causa movimiento en el sistema, sin tener en cuenta la fricción entre la masa y el suelo.
- 📐 Se elabora un diagrama de cuerpo libre para la masa, identificando las fuerzas externas y las reacciones de los resortes.
- ⚖️ Se analiza la interacción de las fuerzas en el eje x, donde la masa se ve afectada por la fuerza externa y las reacciones de los resortes.
- 🔢 Se establece una ecuación de movimiento basada en la suma de fuerzas en el eje x, incluyendo la masa y la aceleración.
- 🔗 Se menciona la ley de Hooke, que relaciona la fuerza de un resorte con su deformación (delta).
- 📉 Se ajusta la ecuación para que los términos negativos se conviertan en positivos, facilitando la comprensión de la relación entre las fuerzas.
- 🔗 Se establece una ecuación diferencial de segundo orden que representa la relación entre la masa, las constantes de los resortes y la fuerza externa.
- 🌐 Se destaca que la ecuación es generalizada y que existen posibles soluciones particulares dependiendo de las constantes de los resortes.
Q & A
¿Qué es el sistema masa- resorte descrito en el video?
-El sistema masa-resorte es un modelo donde una masa está conectada a cuatro resortes que están dispuestos en pares a cada lado de la masa. Estos resortes están sujetos a una fuerza externa que causa movimiento en el sistema.
¿Por qué se supone que el marco de referencia está colocado en el centro de masa del objeto?
-Se coloca el marco de referencia en el centro de masa para simplificar el análisis, ya que se considera que todas las fuerzas actúan a través de este punto, facilitando la aplicación de leyes de Newton.
¿Cuál es la dirección del eje x en el análisis del video?
-En el análisis, el eje x se coloca hacia la derecha, lo que es típico en la mayoría de los análisis, aunque el video también destaca que la dirección del marco de referencia es irrelevante para el problema.
¿Por qué se coloca el eje y hacia abajo en el análisis?
-El eje y se coloca hacia abajo para observar la reacción de los resortes y la masa a la fuerza externa, lo que permite analizar la dinámica del sistema en una dirección específica sin complicaciones adicionales.
¿Qué fuerzas interactúan con la masa en el diagrama de cuerpo libre?
-En el diagrama de cuerpo libre, la masa interactúa con la fuerza externa y las reacciones de los cuatro resortes. Cada resorte genera una fuerza opuesta a la deformación que sufren.
¿Cómo se relaciona la fuerza de un resorte con su deformación según la ley de Hooke?
-La fuerza de un resorte está directamente proporcional a su deformación, según la ley de Hooke, que se expresa como F = -kΔx, donde k es la constante de elasticidad del resorte y Δx es la deformación.
¿Cuál es la ecuación diferencial que se obtiene al analizar las fuerzas en el eje x?
-La ecuación diferencial obtenida es m*a = -(k1*Δx + k2*Δx + k3*Δx + k4*Δx), donde m es la masa, a es la aceleración, y k1, k2, k3, k4 son las constantes de elasticidad de los resortes.
¿Por qué se menciona que la ecuación diferencial es de segundo orden?
-La ecuación diferencial es de segundo orden porque involucra la segunda derivada con respecto al tiempo, que en este caso es la aceleración, lo que indica que la ecuación modela un sistema dinámico complejo.
¿Qué implicaciones tiene que las constantes de elongación de los resortes sean iguales?
-Si las constantes de elongación de los resortes son iguales, se puede simplificar la ecuación diferencial a una forma más compacta, facilitando el análisis y la solución del sistema.
¿Qué se puede inferir de la solución particular del modelo matemático?
-Una solución particular del modelo matemático puede proporcionar una comprensión específica de cómo el sistema se comporta bajo ciertas condiciones, aunque no necesariamente refleje todas las posibles variaciones del sistema.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
5.0 / 5 (0 votes)