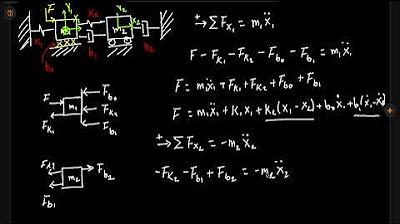Modelado matemático masa resorte amortiguador (Suspensión)
Summary
TLDREste vídeo educativo explica cómo obtener el modelo matemático de una suspensión de vehículo, destacando la importancia de los elementos esenciales como el resorte y el amortiguador. Se describe el proceso de simplificación del fenómeno, establecimiento de restricciones y condiciones iniciales, y la aplicación de la segunda ley de Newton para desarrollar una ecuación diferencial que modela la dinámica del sistema. El enfoque es didáctico, facilitando la comprensión del modelado matemático de sistemas físicos.
Takeaways
- 🔍 El vídeo trata sobre cómo obtener el modelo matemático de una suspensión de vehículo.
- 🔧 Se utilizan dos elementos primordiales en el ejemplo: un resorte y un amortiguador.
- 🚗 La suspensión interactúa con el chasis del vehículo, que contiene la mayoría de la masa.
- 📐 Se hace un esquema simplificado para entender mejor los elementos esenciales del sistema.
- 📏 Se establece que el resorte tiene una constante de elongación y el amortiguador una constante de amortiguamiento.
- 🚫 Se asume que la suspensión solo tiene desplazamiento vertical y se representa con un esquema de rodamientos.
- 🧭 Se establece un marco de referencia en el centro de masa del vehículo para medir direcciones y magnitudes de las fuerzas.
- ⚖️ Se aplica la segunda ley de Newton para establecer la ecuación de movimiento de la suspensión.
- 📉 La fuerza del resorte es proporcional a la deformación y la del amortiguador a la velocidad.
- 💡 Se obtiene una ecuación diferencial que modela el sistema de suspensión, considerando restricciones y condiciones iniciales.
Q & A
¿Qué es un modelo matemático de suspensión y por qué es importante?
-Un modelo matemático de suspensión es una representación abstracta que utiliza ecuaciones y relaciones para describir el comportamiento dinámico de una suspensión de vehículo. Es importante porque permite analizar y predecir cómo responderá el sistema ante diferentes condiciones y cargas, lo que es fundamental para el diseño y la optimización de suspensiones.
¿Cuáles son los elementos primordiales de una suspensión que se mencionan en el guion?
-Los elementos primordiales de una suspensión que se mencionan son el resorte y el amortiguador, que están unidos a una rueda y al chasis del vehículo respectivamente.
¿Qué representa la constante de elongación en un resorte?
-La constante de elongación en un resorte determina la capacidad de formación o deformación que tiene el resorte, es decir, cómo reacciona ante una fuerza aplicando una contrafuerza proporcional a su deformación.
¿Qué es la constante de amortiguamiento y cómo afecta al comportamiento de un amortiguador?
-La constante de amortiguamiento es una medida de la resistencia que ofrece un amortiguador a la vibración o movimiento. Cuanto mayor sea esta constante, mayor será la fuerza que el amortiguador aplicará para reducir la velocidad de un objeto en movimiento, lo que afecta directamente a la suavidad y estabilidad del vehículo.
¿Qué significa que la suspensión solo tenga desplazamiento sobre el eje vertical?
-Esto significa que el modelo asume que la suspensión solo se moverá o se desplazará en dirección vertical, ignorando cualquier movimiento horizontal o rotativo. Esta simplificación ayuda a concentrarse en la dinámica vertical principal que afecta la comodidad y el control del vehículo.
¿Cuál es la segunda condición que se establece para el análisis de la suspensión?
-La segunda condición establecida es iniciar el análisis en condiciones de reposo, lo que significa que el peso del vehículo está completamente compensado por la suspensión, y no hay fuerzas dinámicas iniciales que afecten al sistema.
¿Cómo se determina la dirección de las fuerzas en el modelo matemático?
-En el modelo, se establece que las fuerzas que actúan hacia arriba son positivas y las que actúan hacia abajo son negativas, de acuerdo con la segunda ley de Newton y el marco de referencia establecido en el centro de masa del vehículo.
¿Qué es la ecuación diferencial que modela el sistema de suspensión?
-La ecuación diferencial que modela el sistema de suspensión es: m * x''(t) + c * x'(t) + k * x(t) = F_ext(t), donde m es la masa, c es la constante de amortiguamiento, k es la constante de elongación, x(t) es la posición, x'(t) es la velocidad y x''(t) es la aceleración.
¿Cómo se relaciona la fuerza del amortiguador con la velocidad en el modelo?
-La fuerza del amortiguador en el modelo está directamente proporcional a la velocidad, lo que significa que la fuerza disminuirá o aumentará a medida que la velocidad del movimiento vertical del vehículo cambie.
¿Qué implicaciones tiene el modelo matemático para el diseño de suspensiones?
-El modelo matemático permite a los ingenieros predecir cómo se comportará una suspensión bajo diferentes condiciones y ajustar las constantes de amortiguamiento y elongación para lograr un balance entre la comodidad y el control del vehículo.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тариф5.0 / 5 (0 votes)