El Calculo Integral Aplicado a la Ingenieria Automotriz

Summary

El video explica cómo se aplica la Ley de Hooke en los amortiguadores y suspensiones de los automóviles, centrándose en el cálculo de la fuerza y el trabajo necesario para estirar un resorte. A través de un ejemplo matemático, se demuestra cómo calcular el trabajo realizado para estirar un resorte desde su longitud natural hasta una longitud estirada. Se utiliza el cálculo integral para obtener el trabajo necesario, destacando la importancia de la constante de resorte y los límites de integración para obtener la solución correcta. Este proceso es esencial para garantizar la seguridad y confort en los vehículos.

Takeaways

• 😀 La ley de Hook se aplica a los amortiguadores o suspensiones de los automóviles en una dimensión para entender su funcionamiento básico.
• 😀 Conocer la fuerza que soporta un resorte es esencial para determinar la resistencia a una fuerza externa y garantizar la seguridad y confort de los pasajeros.
• 😀 La ley de Hook nos ayuda a calcular la fuerza necesaria para mantener un resorte estirado una cierta distancia desde su longitud natural.
• 😀 El trabajo realizado por un resorte en la industria automotriz se calcula mediante integrales, utilizando la ley de Hook.
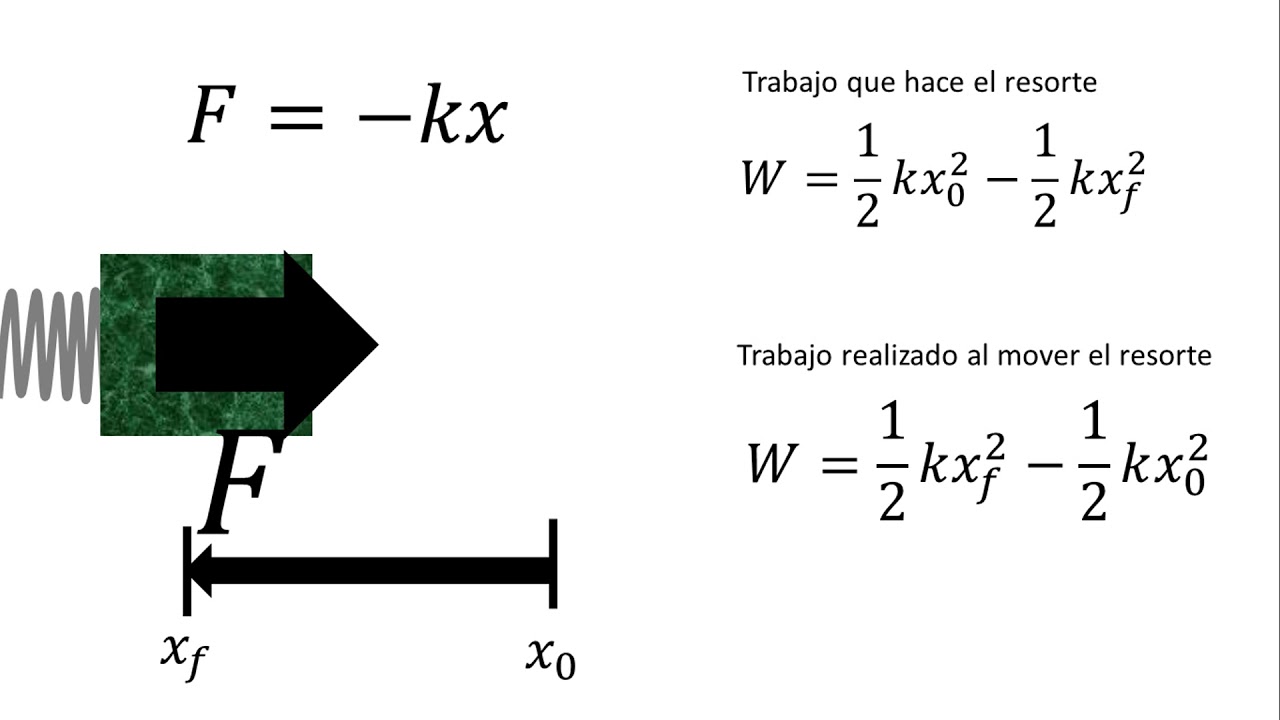
• 😀 En física, la fuerza necesaria para estirar un resorte una cierta distancia está dada por la fórmula F(x) = K * X, donde K es la constante del resorte.
• 😀 La ley de Hook fue formulada originalmente para materiales que experimentan estiramiento longitudinal cuando se les aplica una fuerza.
• 😀 El cálculo del trabajo realizado por un amortiguador dentro de una suspensión se puede obtener mediante el uso de cálculo integral.
• 😀 El problema planteado en el ejemplo es calcular el trabajo necesario para estirar un resorte desde su longitud natural hasta una longitud final.
• 😀 La constante K del resorte se puede escribir como 400, lo que significa que la función de fuerza es F(x) = 400x.
• 😀 La integral se evalúa con los límites de 0 a 0.1, ya que el resorte se estira desde su longitud natural de 0.3 m hasta 0.4 m, lo que equivale a un estiramiento de 0.1 m.
• 😀 Al evaluar la integral de 400x, el trabajo necesario para estirar el resorte se obtiene como 2 J, que es el resultado final del cálculo.

Q & A

¿Qué es la ley de Hook y cómo se aplica a los amortiguadores de un automóvil?

La ley de Hook describe cómo se comporta un resorte cuando se le aplica una fuerza. En el contexto de los amortiguadores de un automóvil, esta ley ayuda a entender la resistencia que un resorte puede ofrecer a una fuerza externa, lo cual es crucial para la seguridad y el confort de los pasajeros.

¿Por qué es importante conocer la fuerza que soporta un resorte en un automóvil?

Es esencial para determinar cuánta resistencia tiene el resorte al aplicar una fuerza externa, lo que afecta directamente la seguridad y el confort de los pasajeros dentro del vehículo.

¿Qué fórmula define la fuerza necesaria para mantener estirado un resorte según la ley de Hook?

La fórmula es F(x) = K * X, donde F(x) es la fuerza necesaria, K es la constante del resorte, y X es la elongación del resorte desde su longitud natural.

¿Qué es la constante K en la ley de Hook y cómo se determina?

La constante K es la constante del resorte, que depende de las características del resorte en particular. En el ejemplo, se puede determinar a partir de los datos proporcionados, como la fuerza necesaria para estirar el resorte a una cierta longitud.

¿Cómo se calcula el trabajo realizado para estirar un resorte según la ley de Hook?

El trabajo realizado se calcula mediante la integral de la fuerza con respecto a la elongación del resorte. Esto se logra aplicando la ley de Hook y evaluando la integral entre los límites de elongación inicial y final.

¿Por qué se utilizan los integrales en el cálculo del trabajo realizado por un resorte?

El uso de integrales permite calcular el trabajo realizado a medida que el resorte se estira, considerando que la fuerza cambia continuamente con la elongación del resorte. Esto proporciona una estimación precisa del trabajo total.

¿Qué significa la integral F(x) = 400x en el contexto del ejercicio?

La integral F(x) = 400x se refiere a la fuerza que el resorte ejerce en función de su elongación. La constante 400 es la constante K determinada en el ejercicio, y x representa la elongación del resorte en metros.

¿Por qué los límites de la integral son 0 y 0.1 metros en el ejercicio?

Los límites de integración se determinan porque el resorte tiene una longitud natural de 0.3 m y se estira hasta 0.4 m, lo que implica una elongación de 0.1 m. Por lo tanto, los límites de integración son de 0 a 0.1 metros.

¿Qué resultado se obtiene al evaluar la integral en este ejercicio?

Al evaluar la integral de 400x desde 0 hasta 0.1 metros, se obtiene que el trabajo necesario para estirar el resorte es de 2 julios.

¿Por qué es importante asegurarse de que la constante K y los límites de integración sean correctos en este ejercicio?

Es fundamental porque un valor incorrecto de la constante K o de los límites de integración afectaría el cálculo del trabajo realizado, lo que llevaría a un resultado erróneo en la estimación del esfuerzo necesario para estirar el resorte.