GCSE Maths - How to find the Area of Compound Shapes #106
Summary
TLDRThis educational video teaches viewers how to calculate the area of irregular shapes by breaking them down into simpler geometric figures like rectangles, triangles, parallelograms, and trapeziums. The script illustrates the process with examples, showing how to find areas by using basic formulas for these shapes. It guides through calculating the area of a rectangle and a triangle combined, and then a rectangle and a trapezium, highlighting the importance of understanding how to decompose complex shapes into manageable parts for area calculation.
Takeaways
- 📏 To find the area of irregular shapes, they must be divided into smaller, recognizable shapes like rectangles, parallelograms, triangles, and trapeziums.
- 🔢 The formulas for calculating areas of simple shapes are essential: length x width for rectangles, base x height / 2 for triangles, and (a + b) / 2 x height for trapeziums.
- 🔍 For composite shapes, identify and calculate the area of each simple shape component and then sum them to get the total area.
- 📐 When a shape includes a triangle, calculate its height if not given by subtracting the height of any included rectangles from the total height.
- 📈 The example in the script demonstrates how to decompose a shape into a rectangle and a triangle, calculate their areas separately, and then add them to find the total area.
- 📉 Another example shows how to handle a shape with a trapezium on top by first calculating the area of the rectangle and then the trapezium using the average of the parallel sides.
- 📝 The script emphasizes the importance of understanding how to break down complex shapes into simple ones for area calculation.
- 🎯 The video provides a practical approach to solving area problems by visually demonstrating the process with specific examples.
- 💡 The tips shared are useful for students or anyone needing to calculate areas of irregular shapes for mathematical, architectural, or artistic purposes.
- 📚 The video encourages viewers to visit a live past paper website for additional educational resources, enhancing learning opportunities.
Q & A
What is the main challenge when calculating the area of irregular shapes?
-The main challenge is that irregular shapes don't have their own formulas like rectangles or triangles do, so they need to be divided into smaller, familiar shapes to calculate their areas.
What are the four basic shapes whose area formulas we need to know for this process?
-The four basic shapes are rectangles, parallelograms, triangles, and trapeziums, as they have known area formulas.
How can you split a complex shape into simpler shapes to calculate its area?
-You can split a complex shape by drawing lines to create rectangles, triangles, trapeziums, or parallelograms, whose areas can be calculated using known formulas.
What is the formula for the area of a rectangle?
-The formula for the area of a rectangle is length times width.
How do you calculate the area of a triangle?
-The area of a triangle is calculated using the formula one half times base times height.
In the example given, why is the height of the triangle 3 centimeters?
-The height of the triangle is 3 centimeters because the total height of the shape is 7 centimeters, and the rectangle at the bottom takes up 4 centimeters of that height.
How do you find the total area of a compound shape after calculating the areas of its parts?
-You find the total area of a compound shape by adding together the areas of each of its simpler shapes.
What is the area of the rectangle in the second example of the script?
-The area of the rectangle in the second example is 180 square centimeters, calculated by multiplying the length (15 cm) by the width (12 cm).
How is the area of a trapezium calculated according to the script?
-The area of a trapezium is calculated by finding the average of the two parallel sides (a + b)/2 and then multiplying by the height.
In the script, what is the total area of the second compound shape after breaking it down into a rectangle and a trapezium?
-The total area of the second compound shape is 205 square centimeters, which is the sum of the rectangle's area (180 cm²) and the trapezium's area (25 cm²).
What additional resource is mentioned at the end of the script for further practice?
-At the end of the script, a live past paper website is mentioned where viewers can practice similar problems.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

MATERI UTBK SNBT PENALARAN MATEMATIKA - BANGUN DATAR
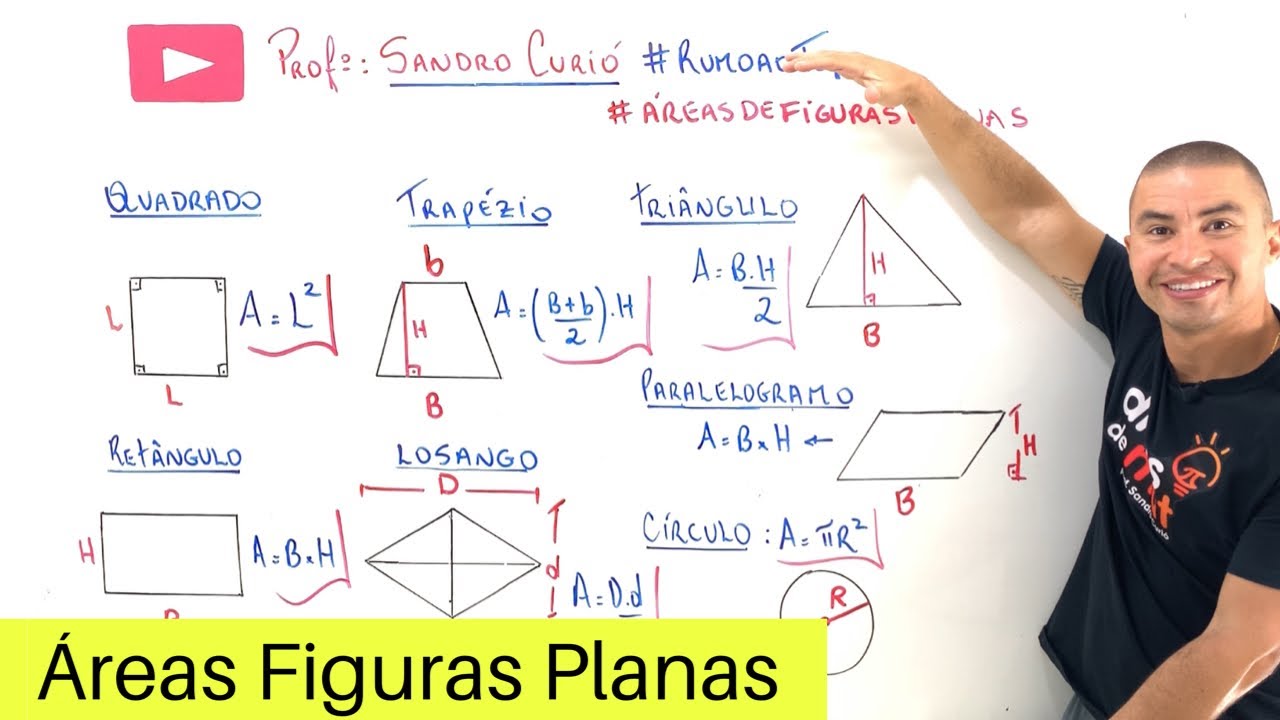
ÁREA DAS PRINCIPAIS FIGURAS PLANAS | GEOMETRIA PLANA
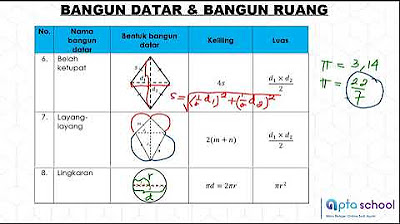
MATERI BANGUN DATAR DAN RUANG

Math 5 Quarter 1 Week 6 Revised K-12 Area Of A Parallelogram, Triangle, And Trapezoid
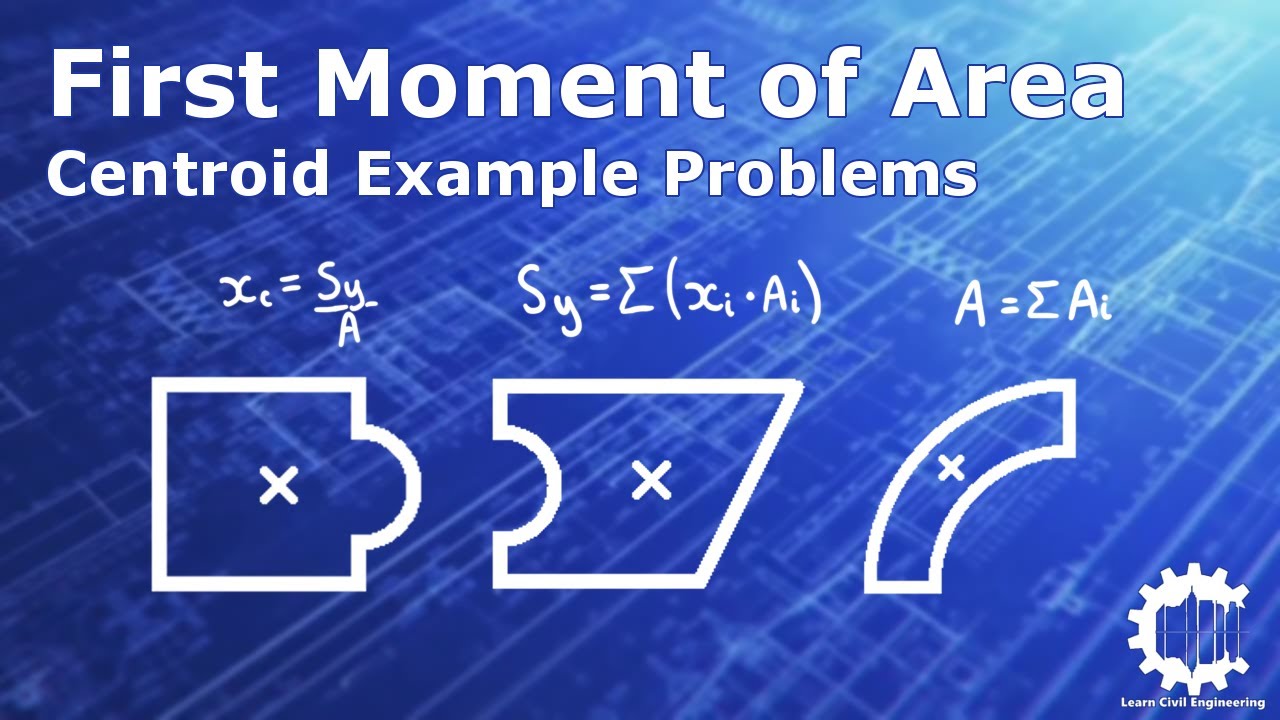
Finding the Centroid with First Moment of Area Example Problems - Structural Analysis

Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geometry
5.0 / 5 (0 votes)
