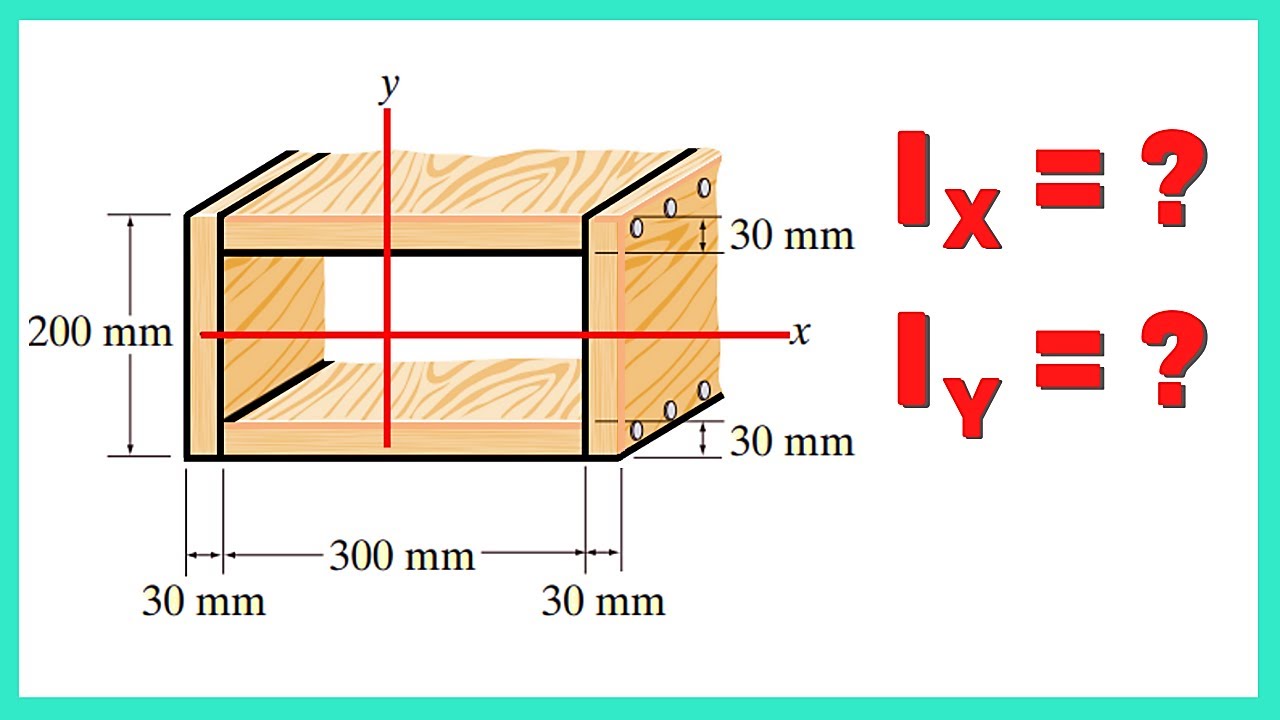
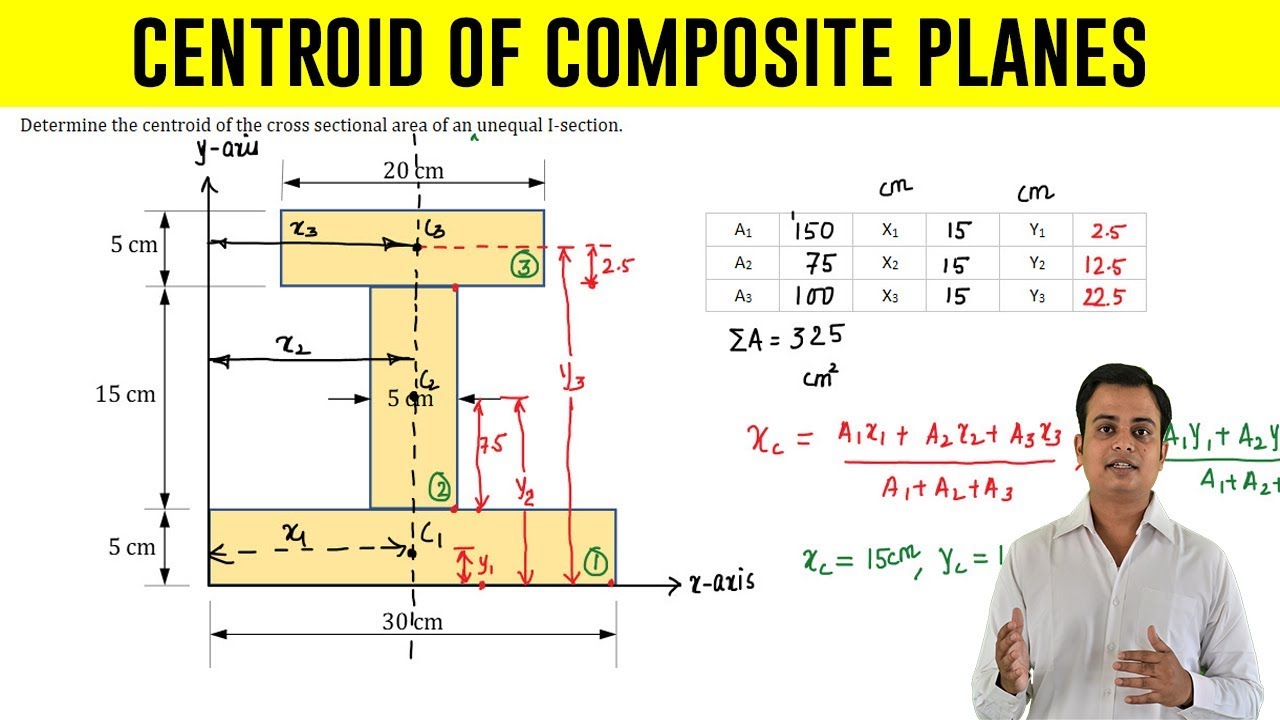
Finding the Centroid with First Moment of Area Example Problems - Structural Analysis
Summary
TLDRIn this video by Learn Civil Engineering, the concept of the first moment of area is used to determine the centroid of complex regions. Through detailed examples, viewers learn how to break down irregular shapes into simpler components like squares, triangles, and quarter circles to calculate centroids using key formulas. The video covers step-by-step calculations, applying symmetry for efficiency, and demonstrates practical applications in engineering. It serves as a valuable resource for understanding how to find the centroid of composite shapes and encourages viewers to practice these techniques on their own.
Takeaways
- 😀 The first moment of area is a critical concept for determining the centroid of complex regions in civil engineering.
- 😀 To calculate the centroid of a compound shape, you need to break the region into simpler sections (like squares, triangles, or circles) and apply the first moment of area formula.
- 😀 The first moment of area relative to the y-axis (S_y) is calculated by summing the product of the centroid's x-coordinate and the area of each section.
- 😀 The x-coordinate of the centroid of a complex region is the first moment of area (S_y) divided by the total area of the region.
- 😀 The centroid of a simple rectangle is located at half of its base for the x-coordinate and half of its height for the y-coordinate.
- 😀 For a triangle, the centroid's y-coordinate is at one-third of its height from the base, and its x-coordinate depends on the shape's geometry.
- 😀 A quarter circle's centroid can be determined using the formula 4r / (3π), where r is the radius, and this is applicable for both x and y coordinates depending on the region's orientation.
- 😀 Symmetry can often simplify calculations by providing an immediate understanding of the centroid's location without complex computations.
- 😀 In example problems, the areas of each region (such as squares, triangles, or circles) and their respective centroids are used to compute the overall centroid of the composite region.
- 😀 The method of using the first moment of area is applicable to complex shapes involving sections like quarter circles, with appropriate adjustments for mirrored sections or removed areas.
Q & A
What is the concept of the first moment of area, and how is it used to determine the centroid?
-The first moment of area refers to the product of the area of a region and the distance from a reference axis. It is used to calculate the location of the centroid of a complex shape by finding the balance point of the area relative to a chosen axis. Specifically, the x-coordinate of the centroid is found by dividing the first moment of area relative to the y-axis by the total area.
How do you calculate the x-coordinate of the centroid for a complex region made of multiple shapes?
-The x-coordinate of the centroid for a complex region is calculated by summing the products of the x-coordinate of the centroid of each individual region and its area, then dividing by the total area of the complex region.
What is the formula for the centroid of a quarter circle, and how is it applied in example 1?
-The formula for the centroid of a quarter circle is given by (4r / 3π), where r is the radius. In example 1, the centroids of two quarter circles are calculated using this formula to determine their x-coordinates, which are then used to find the overall centroid of the entire complex shape.
Why is the centroid of region 1 in example 1 at x = 10 and y = 10?
-Region 1 in example 1 is a square, and the centroid of a square is located at the center. Since the side length of the square is 20 mm, the centroid lies at the midpoint of each side, which is 10 mm from both the x and y axes.
In example 1, how do the x-coordinates of regions 2 and 3 relate to each other?
-Regions 2 and 3 are symmetrical, and their x-coordinates of the centroids are the same (22.12 mm) because the shapes are identical but mirrored along the line y = 10.
How do symmetry properties help in solving the centroid for complex regions, as demonstrated in example 2?
-Symmetry allows for simplification of calculations. In example 2, the symmetry of the region about the line y = 10 means the y-coordinate of the centroid is already known to be 10 mm without further calculation, reducing the complexity of the problem.
What is the significance of dividing a complex region into smaller regions when calculating the centroid?
-Dividing a complex region into smaller, simpler shapes allows for the application of known centroid formulas for basic shapes. This makes the overall calculation of the centroid more manageable, as it involves summing the centroids of the individual regions weighted by their areas.
What is the relationship between the first moment of area and the location of the centroid?
-The first moment of area is a measure of how the area is distributed relative to an axis. The location of the centroid is determined by dividing the first moment of area by the total area. This gives the average position of the area with respect to the axis.
Why is it important to establish coordinate axes when calculating the centroid?
-Establishing coordinate axes provides a reference point for all measurements and calculations. The centroid’s coordinates are determined relative to these axes, making it easier to compute the centroid's location for complex regions.
How does the calculation of the centroid change when dealing with a region with shapes removed, as in example 2?
-When dealing with regions with shapes removed, the areas of the removed shapes are subtracted from the total area, and their centroids are subtracted accordingly in the first moment of area calculations. This modifies the final centroid location compared to a simple addition of areas.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)