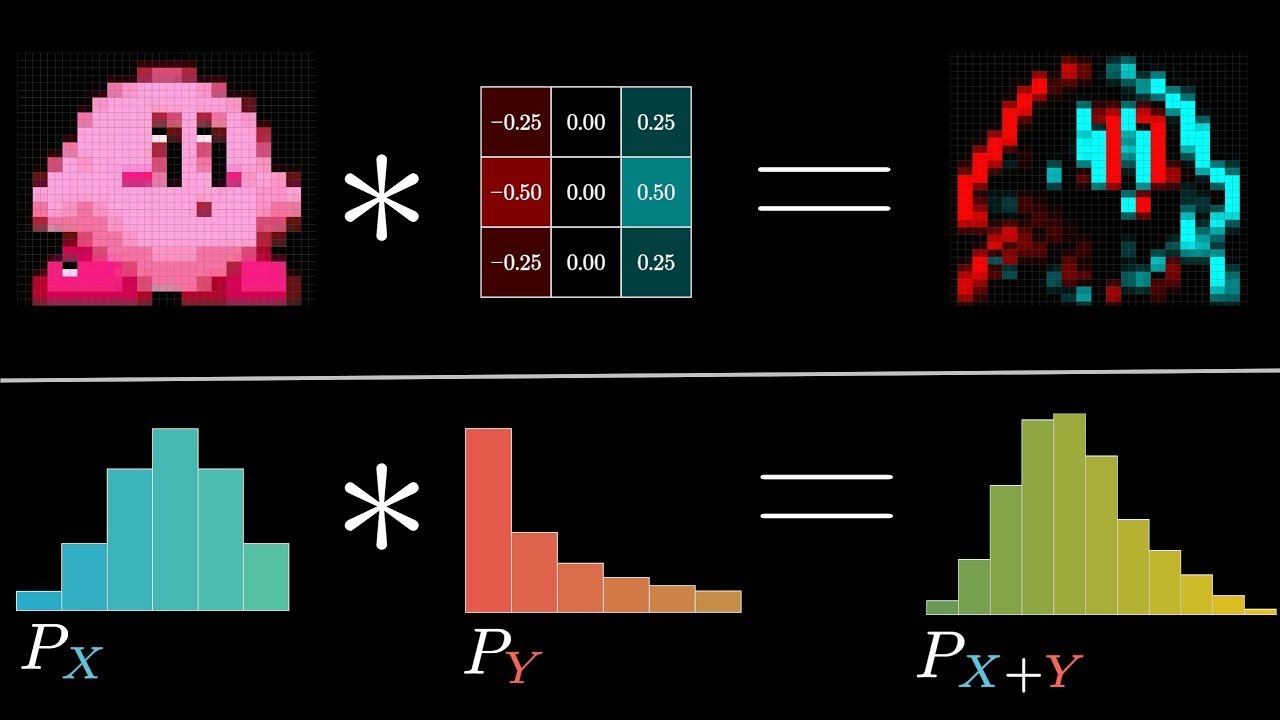
But what is a convolution?

Summary

このビデオスクリプトでは、異なる数値リストや関数を組み合わせる方法の一つとして、あまり一般的でないが基本的な「畳み込み」に焦点を当てています。畳み込みは画像処理、確率論、微分方程式の解法など、多岐にわたる分野で重要な役割を果たしています。具体的には、2つのサイコロの確率分布を畳み込む例や、ポリノミアルの乗算、移動平均、画像のぼかし効果などの計算方法を通じて、畳み込みの直感的な理解を深めることを目指しています。さらに、高速フーリエ変換を利用した畳み込みの効率的な計算方法についても触れ、数学が多様な分野でどのように応用されるかを示しています。

Takeaways

• 😀 Convolution is a fundamental way to combine two lists or functions
• 😀 Useful in many areas like image processing, probability, differential equations
• 😀 Can visualize as sliding windows or table of products
• 😀 Blurring images is like a weighted moving average
• 😀 Choosing different kernels gives different effects
• 😀 Connected to multiplying polynomials and collecting terms
• 😀 Using FFTs gives a faster convolution algorithm
• 😀 Leverages structure of roots of unity evaluation points
• 😀 Speedup helps many applications needing convolution
• 😀 Even relates to standard multiplication of numbers

Q & A

畳み込みとは何ですか？

畳み込みは、二つのリストや関数を組み合わせて新しいリストや関数を生成する方法の一つであり、各項を個別に加算や乗算する以外の方法で、一方の配列を反転させて他方との各項の積を取り、それらを加算して新しいシーケンスを作成します。

畳み込みの応用分野はどこにありますか？

畳み込みは画像処理、確率論、微分方程式の解法など、多岐にわたる分野で広く使用されています。特に、多項式の乗算において畳み込みが自然に現れます。

畳み込みが確率論でどのように使用されるかの具体例は？

畳み込みは、異なる確率分布の合成を計算する際に使用されます。例えば、二つのサイコロを振ったときの目の和の確率分布を求めることができます。

畳み込みを計算するためのアルゴリズムは？

畳み込みを計算するためのアルゴリズムには、直接的な方法と、FFT（高速フーリエ変換）を利用した方法があります。FFTを用いた方法は計算効率が良く、特に大きなデータセットに対して高速に畳み込みを計算できます。

畳み込みの直感的な理解はどのように得られますか？

畳み込みの直感的な理解は、一方の配列を反転させ、それを他方の配列に沿ってスライドさせながら、重なる部分の要素同士を乗算し、その積を加算することで新しい配列を生成するプロセスを可視化することで得られます。

画像処理における畳み込みの役割は？

画像処理において、畳み込みは画像の平滑化（ブラーリング）、エッジ検出、シャープ化などの効果を実現するために使用されます。これは、特定のカーネル（小さな行列）を画像全体に適用することで行われます。

畳み込みニューラルネットワークとは何ですか？

畳み込みニューラルネットワーク（CNN）は、畳み込みの概念を利用した深層学習のモデルの一つで、特に画像認識や音声認識などの分野で優れた性能を発揮します。CNNは、データから自動的に特徴を抽出する能力を持っています。

多項式の乗算に畳み込みがどのように関連しているか？

多項式の乗算は、その係数の畳み込みによって計算できます。これは、多項式の各項を乗算し、同じ次数の項を加算するプロセスが、畳み込みの定義と一致するためです。

畳み込みの出力の長さはどのように決まりますか？

畳み込みの出力の長さは、入力された二つの配列の長さに依存します。一般的に、出力の長さは入力配列の長さの合計から1を引いたものになります。ただし、実際の応用では出力を特定の長さに調整するために切り捨てやパディングが行われることがあります。

畳み込みを利用したアルゴリズムの計算効率について説明してください。

畳み込みを直接計算する方法は一般にO(n^2)の計算量がかかりますが、FFTを利用した畳み込み計算はO(n log n)の計算量で済み、大規模なデータに対してはこの方法が非常に効率的です。

Outlines

00:00

🔍 畳み込みの基本

畳み込みは、数列や関数を組み合わせて新しい数列や関数を生成する方法の一つで、画像処理、確率論、微分方程式の解法など様々な場面で用いられる。畳み込みは数に対する操作から直接継承されるものではなく、数列や関数の組み合わせにおいて新たに生じる操作であり、多項式の乗算などで見られる。このビデオでは、畳み込みの直感的な理解と、離散ケースにおける計算方法に焦点を当て、連続ケースは後続のパートで扱う。

05:05

📊 確率と畳み込みの応用

畳み込みの概念は、異なる確率分布の加算や画像の移動平均など、多岐にわたる応用が可能である。特に、サイコロを例に取り、畳み込みを用いて異なる和が出る確率を計算する方法を説明し、確率分布の加算における畳み込みの重要性を示す。また、画像処理における畳み込みの利用例として、平滑化（ブラリング）に焦点を当て、異なる重み付けを行うことでさまざまな効果を生み出すことができることを説明する。

10:06

🖼️ 画像処理における畳み込み

画像処理における畳み込みの応用は多岐にわたり、ガウシアン分布を用いたブラリングから、エッジ検出や画像の鮮明化など、異なるカーネルを使用することで多様な効果が得られる。畳み込みニューラルネットワークでは、これらのカーネルをデータに基づいて自動的に学習させることができ、画像認識や分類に革命をもたらしている。また、畳み込みの出力サイズやカーネルの反転といった、コンピュータサイエンスにおける特定の実装上の選択が、純粋数学からの概念をどのように補完しているかを示す。

15:08

🧮 多項式の乗算と畳み込み

多項式の乗算は畳み込みの一形態であり、異なる多項式の係数リストを畳み込むことで、係数の畳み込みが多項式の乗算に等しいことを示す。この関連性は、畳み込みが点ごとの乗算より計算上複雑であることを示唆しているが、多項式の乗算における畳み込みの効率的なアルゴリズムの開発につながる。

20:11

💡 FFTを用いた畳み込みの高速化

FFT（高速フーリエ変換）を用いることで、畳み込みを効率的に計算することが可能になる。この方法は、畳み込みを実行する際の計算量を大幅に削減し、n log n のオーダーに改善する。FFTは多項式の乗算だけでなく、確率分布の加算や大規模な画像処理など、畳み込みが関係するさまざまな問題に応用できる。このビデオでは、FFTを使った畳み込みの計算方法とその重要性について解説し、畳み込みが数学の多様な分野でどのように役立つかを示している。

Keywords

💡畳み込み

2つの数列や関数を組み合わせて新しい数列や関数を作る操作。画像処理や確率分布の計算などでよく使われる。スクリプトではサイコロの例などを通じて説明している。

💡確率分布

それぞれの出来事が起こる確率を表す分布。スクリプトではサイコロの目の組み合わせごとの確率を畳み込みで計算する例を示している。

💡画像処理

デジタル画像に様々な処理を施すこと。スクリプトでは畳み込みを使ったぼかし処理などの例を示している。

💡多項式

複数の項からなる式。スクリプトでは2つの多項式を掛け合わせることが畳み込みと等価であることを説明している。

💡高速フーリエ変換

信号処理で使われるアルゴリズム。畳み込みを効率的に計算するのに使える。スクリプトではこれを使って畳み込みを高速に計算する方法を示している。

💡カーネル

画像処理でフィルタとして使われる小さい行列。スクリプトではエッジ検出などの例を示している。

💡移動平均

時系列データを平滑化する技法。スクリプトではこれも畳み込みの一例として示している。

💡ガウス分布

正規分布のこと。画像処理のぼかしでよく使われる。スクリプトでもガウス分布に基づくぼかしの例を紹介している。

💡畳み込みニューラルネットワーク

画像認識などで使われるニューラルネットワークの一種。名前の通り畳み込みを特徴抽出に利用している。スクリプトではごく簡単に言及している。

💡フーリエ変換

信号処理などで使われる解析手法。スクリプトでは高速フーリエ変換との関連性を説明している。

Highlights

Convolutions show up in many areas like image processing, probability theory, solving differential equations.

Convolutions can be used for operations like moving averages or blurring images.

Convolutions can also detect edges in images by using particular kernel values.

Multiplying polynomials is equivalent to convolving their coefficients.

The FFT algorithm provides a fast way to compute convolutions in O(n log n) time.

Transcripts

Suppose I give you two different lists of numbers, or maybe two different functions,

and I ask you to think of all the ways you might combine those two lists to get

a new list of numbers, or combine the two functions to get a new function.

Maybe one simple way that comes to mind is to simply add them together term by term.

Likewise with the functions, you can add all the corresponding outputs.

In a similar vein, you could also multiply the two lists

term by term and do the same thing with the functions.

But there's another kind of combination just as fundamental as both of those,

but a lot less commonly discussed, known as a convolution.

But unlike the previous two cases, it's not something that's

merely inherited from an operation you can do to numbers.

It's something genuinely new for the context of lists of numbers or combining functions.

They show up all over the place, they are ubiquitous in image processing,

it's a core construct in the theory of probability,

they're used a lot in solving differential equations,

and one context where you've almost certainly seen it, if not by this name,

is multiplying two polynomials together.

As someone in the business of visual explanations, this is an especially great topic,

because the formulaic definition in isolation and without context can look kind of

intimidating, but if we take the time to really unpack what it's saying,

and before that actually motivate why you would want something like this,

it's an incredibly beautiful operation.

And I have to admit, I actually learned a little something

while putting together the visuals for this project.

In the case of convolving two different functions,

I was trying to think of different ways you might picture what that could mean,

and with one of them I had a little bit of an aha moment for why it is that

normal distributions play the role that they do in probability,

why it's such a natural shape for a function.

But I'm getting ahead of myself, there's a lot of setup for that one.

In this video, our primary focus is just going to be on the discrete case,

and in particular building up to a very unexpected but very clever algorithm for

computing these.

And I'll pull out the discussion for the continuous case into a second part.

It's very tempting to open up with the image processing examples,

since they're visually the most intriguing, but there are a couple bits of finickiness

that make the image processing case less representative of convolutions overall,

so instead let's kick things off with probability,

and in particular one of the simplest examples that I'm sure everyone here has

thought about at some point in their life, which is rolling a pair of dice and

figuring out the chances of seeing various different sums.

And you might say, not a problem, not a problem.

Each of your two dice has six different possible outcomes,

which gives us a total of 36 distinct possible pairs of outcomes,

and if we just look through them all we can count up how many pairs have a given sum.

And arranging all the pairs in a grid like this,

one pretty nice thing is that all of the pairs that have a constant sum are visible

along one of these different diagonals.

So simply counting how many exist on each of those diagonals

will tell you how likely you are to see a particular sum.

And I'd say, very good, very good, but can you think of

any other ways that you might visualize the same question?

Other images that can come to mind to think of

all the distinct pairs that have a given sum?

And maybe one of you raises your hand and says, yeah, I've got one.

Let's say you picture these two different sets of possibilities each in a row,

but you flip around that second row.

That way all of the different pairs which add up to seven line up vertically like this.

And if we slide that bottom row all the way to the right,

then the unique pair that adds up to two, the snake eyes, are the only ones that align,

and if I schlunk that over one unit to the right,

the pairs which align are the two different pairs that add up to three.

And in general, different offset values of this lower array,

which remember I had to flip around first, reveal all the distinct pairs that

have a given sum.

As far as probability questions go, this still isn't especially interesting because

all we're doing is counting how many outcomes there are in each of these categories.

But that is with the implicit assumption that there's

an equal chance for each of these faces to come up.

But what if I told you I have a special set of dice that's not uniform?

Maybe the blue die has its own set of numbers describing the probabilities for

each face coming up, and the red die has its own unique distinct set of numbers.

In that case, if you wanted to figure out, say,

the probability of seeing a 2, you would multiply the probability

that the blue die is a 1 times the probability that the red die is a 1.

And for the chances of seeing a 3, you look at the two distinct

pairs where that's possible, and again multiply the corresponding

probabilities and then add those two products together.

Similarly, the chances of seeing a 4 involves multiplying together

three different pairs of possibilities and adding them all together.

And in the spirit of setting up some formulas, let's name these top probabilities a 1,

a 2, a 3, and so on, and name the bottom ones b 1, b 2, b 3, and so on.

And in general, this process where we're taking two different arrays of numbers,

flipping the second one around, and then lining them up at various different

offset values, taking a bunch of pairwise products and adding them up,

that's one of the fundamental ways to think about what a convolution is.

So just to spell it out a little more exactly, through this process,

we just generated probabilities for seeing 2, 3, 4, on and on up to 12,

and we got them by mixing together one list of values, a, and another list of values, b.

In the lingo, we'd say the convolution of those two sequences gives us this new sequence,

the new sequence of 11 values, each of which looks like some sum of pairwise products.

If you prefer, another way you could think about the same operation is to first

create a table of all the pairwise products, and then add up along all these diagonals.

Again, that's a way of mixing together these two

sequences of numbers to get us a new sequence of 11 numbers.

It's the same operation as the sliding windows thought, just another perspective.

Putting a little notation to it, here's how you might see it written down.

The convolution of a and b, denoted with this little asterisk, is a new list,

and the nth element of that list looks like a sum,

and that sum goes over all different pairs of indices, i and j,

so that the sum of those indices is equal to n.

It's kind of a mouthful, but for example, if n was 6,

the pairs we're going over are 1 and 5, 2 and 4, 3 and 3, 4 and 2, 5 and 1,

all the different pairs that add up to 6.

But honestly, however you write it down, the notation is secondary in

importance to the visual you might hold in your head for the process.

Here, maybe it helps to do a super simple example,

where I might ask you what's the convolution of the list 1, 2, 3 with the list 4, 5, 6.

You might picture taking both of these lists, flipping around that second one,

and then starting with its lid all the way over to the left.

Then the pair of values which align are 1 and 4,

multiply them together, and that gives us our first term of our output.

Slide that bottom array one unit to the right,

the pairs which align are 1, 5 and 2 and 4, multiply those pairs,

add them together, and that gives us 13, the next entry in our output.

Slide things over once more, and we'll take 1 times 6 plus 2 times 5 plus 3 times 4,

which happens to be 28.

One more slide and we get 2 times 6 plus 3 times 5, and that gives us 27.

And finally the last term will look like 3 times 6.

If you'd like, you can pull up whatever your favorite programming

language is and your favorite library that includes various numerical operations,

and you can confirm I'm not lying to you.

If you take the convolution of 1, 2, 3 against 4,

5, 6, this is indeed the result that you'll get.

We've seen one case where this is a natural and desirable operation,

adding up to probability distributions, and another common example would be a

moving average.

Imagine you have some long list of numbers, and you take

another smaller list of numbers that all add up to 1.

In this case, I just have a little list of 5 values and they're all equal to 1 5th.

Then if we do this sliding window convolution process,

and kind of close our eyes and sweep under the rug what happens at

the very beginning of it, once our smaller list of values entirely

overlaps with the bigger one, think about what each term in this convolution really means.

At each iteration, what you're doing is multiplying each of the values

from your data by 1 5th and adding them all together,

which is to say you're taking an average of your data inside this little window.

Overall, the process gives you a smoothed out version of the original data,

and you could modify this starting with a different little list of numbers,

and as long as that little list all adds up to 1,

you can still interpret it as a moving average.

In the example shown here, that moving average

would be giving more weight towards the central value.

This also results in a smoothed out version of the data.

If you do kind of a two-dimensional analog of this,

it gives you a fun algorithm for blurring a given image.

And I should say the animations I'm about to show are modified from something

I originally made for part of a set of lectures I did with the Julia lab at

MIT for a certain open courseware class that included an image processing unit.

There we did a little bit more to dive into the code behind all of this,

so if you're curious, I'll leave you some links.

But focusing back on this blurring example, what's going on is I've got this

little 3x3 grid of values that's marching along our original image, and if we zoom in,

each one of those values is 1 9th, and what I'm doing at each iteration is

multiplying each of those values by the corresponding pixel that it sits on top of.

And of course in computer science, we think of colors as little vectors of three values,

representing the red, green, and blue components.

When I multiply all these little values by 1 9th and I add them together,

it gives us an average along each color channel,

and the corresponding pixel for the image on the right is defined to be that sum.

The overall effect, as we do this for every single pixel on the image,

is that each one kind of bleeds into all of its neighbors,

which gives us a blurrier version than the original.

In the lingo, we'd say that the image on the right is a

convolution of our original image with a little grid of values.

Or more technically, maybe I should say that it's the convolution

with a 180 degree rotated version of that little grid of values.

Not that it matters when the grid is symmetric,

but it's just worth keeping in mind that the definition of a convolution,

as inherited from the pure math context, should always invite you to think about

flipping around that second array.

If we modify this slightly, we can get a much more elegant

blurring effect by choosing a different grid of values.

In this case, I have a little 5x5 grid, but the distinction is not so much its size.

If we zoom in, we notice that the value in the middle

is a lot bigger than the value towards the edges.

And where this is coming from is they're all sampled from a bell curve,

known as a Gaussian distribution.

That way, when we multiply all of these values by the corresponding

pixel that they're sitting on top of, we're giving a lot more weight

to that central pixel, and much less towards the ones out at the edge.

And just as before, the corresponding pixel on the right is defined to be this sum.

As we do this process for every single pixel, it gives a blurring effect,

which much more authentically simulates the notion of putting your lens out of focus,

or something like that.

But blurring is far from the only thing that you can do with this idea.

For instance, take a look at this little grid of values,

which involves some positive numbers on the left,

and some negative numbers on the right, which I'll color with blue and red respectively.

Take a moment to see if you can predict and understand

what effect this will have on the final image.

So in this case, I'll just be thinking of the image as grayscale instead of colored,

so each of the pixels is just represented by one number instead of three.

And one thing worth noticing is that as we do this convolution,

it's possible to get negative values.

For example, at this point here, if we zoom in,

the left half of our little grid sits entirely on top of black pixels,

which would have a value of zero, but the right half of negative values all sit on

top of white pixels, which would have a value of one.

So when we multiply corresponding terms and add them together,

the results will be very negative.

And the way I'm displaying this with the image on the right

is to color negative values red and positive values blue.

Another thing to notice is that when you're on a patch that's all the same color,

everything goes to zero, since the sum of the values in our little grid is zero.

This is very different from the previous two examples where the sum of our little

grid was one, which let us interpret it as a moving average and hence a blur.

All in all, this little process basically detects wherever there's

variation in the pixel value as you move from left to right,

and so it gives you a kind of way to pick up on all the vertical edges from your image.

And similarly, if we rotated that grid around so that it varies as you move from

the top to the bottom, this will be picking up on all the horizontal edges,

which in the case of our little pie creature image does result in some pretty

demonic eyes.

This smaller grid, by the way, is often called a kernel,

and the beauty here is how just by choosing a different kernel,

you can get different image processing effects, not just blurring your edge detection,

but also things like sharpening.

For those of you who have heard of a convolutional neural network,

the idea there is to use data to figure out what the kernels should be in

the first place, as determined by whatever the neural network wants to detect.

Another thing I should maybe bring up is the length of the output.

For something like the moving average example,

you might only want to think about the terms when both of the windows

fully align with each other.

Or in the image processing example, maybe you want

the final output to have the same size as the original.

Now, convolutions as a pure math operation always produce an

array that's bigger than the two arrays that you started with,

at least assuming one of them doesn't have a length of one.

Just know that in certain computer science contexts,

you often want to deliberately truncate that output.

Another thing worth highlighting is that in the computer science context,

this notion of flipping around that kernel before you let it march across

the original often feels really weird and just uncalled for, but again,

note that that's what's inherited from the pure math context,

where like we saw with the probabilities, it's an incredibly natural thing to do.

And actually, I can show you one more pure math example where

even the programmers should care about this one,

because it opens the doors for a much faster algorithm to compute all of these.

To set up what I mean by faster here, let me go back and pull up some Python again,

and I'm going to create two different relatively big arrays.

Each one will have a hundred thousand random elements in it,

and I'm going to assess the runtime, of the convolve function from the NumPy library.

And in this case, it runs it for multiple different iterations, tries to find an average,

and it looks like, on this computer at least, it averages at 4.87 seconds.

By contrast, if I use a different function from the SciPy library called fftConvolve,

which is the same thing just implemented differently,

that only takes 4.3 milliseconds on average, so three orders of magnitude improvement.

And again, even though it flies under a different name,

it's giving the same output that the other convolve function does,

it's just doing something to go about it in a cleverer way.

Remember how with the probability example, I said another way you could

think about the convolution was to create this table of all the pairwise products,

and then add up those pairwise products along the diagonals.

There's of course nothing specific to probability.

Any time you're convolving two different lists of numbers,

you can think about it this way.

Create this kind of multiplication table with all pairwise products,

and then each sum along the diagonal corresponds to one of your final outputs.

One context where this view is especially natural

is when you multiply together two polynomials.

For example, let me take the little grid we already have and replace the top terms

with 1, 2x, and 3x squared, and replace the other terms with 4, 5x, and 6x squared.

Now, think about what it means when we're creating all of

these different pairwise products between the two lists.

What you're doing is essentially expanding out the full product of

the two polynomials I have written down, and then when you add up along the diagonal,

that corresponds to collecting all like terms.

Which is pretty neat.

Expanding a polynomial and collecting like terms

is exactly the same process as a convolution.

But this allows us to do something that's pretty cool,

because think about what we're saying here.

We're saying if you take two different functions and you multiply them together,

which is a simple pointwise operation, that's the same thing as if you had

first extracted the coefficients from each one of those, assuming they're polynomials,

and then taken a convolution of those two lists of coefficients.

What makes that so interesting is that convolutions feel,

in principle, a lot more complicated than simple multiplication.

And I don't just mean conceptually they're harder to think about.

I mean, computationally, it requires more steps to perform a convolution

than it does to perform a pointwise product of two different lists.

For example, let's say I gave you two really big polynomials,

say each one with a hundred different coefficients.

Then if the way you multiply them was to expand out this product,

you know, filling in this entire 100 by 100 grid of pairwise products,

that would require you to perform 10,000 different products.

And then, when you're collecting all the like terms along the diagonals,

that's another set of around 10,000 operations.

More generally, in the lingo, we'd say the algorithm is O of n squared,

meaning for two lists of size n, the way that the number of

operations scales is in proportion to the square of n.

On the other hand, if I think of two polynomials in terms of their outputs, for example,

sampling their values at some handful of inputs,

then multiplying them only requires as many operations as the number of samples,

since again, it's a pointwise operation.

And with polynomials, you only need finitely many

samples to be able to recover the coefficients.

For example, two outputs are enough to uniquely specify a linear polynomial,

three outputs would be enough to uniquely specify a quadratic polynomial,

and in general, if you know n distinct outputs,

that's enough to uniquely specify a polynomial that has n different coefficients.

Or, if you prefer, we could phrase this in the language of systems of equations.

Imagine I tell you I have some polynomial, but I don't tell you what the coefficients are.

Those are a mystery to you.

In our example, you might think of this as the product that we're trying to figure out.

And then, suppose I say, I'll just tell you what the outputs of this polynomial

would be if you inputted various different inputs, like 0, 1, 2, 3, on and on,

and I give you enough so that you have as many equations as you have unknowns.

It even happens to be a linear system of equations, so that's nice,

and in principle, at least, this should be enough to recover the coefficients.

So the rough algorithm outline then would be, whenever you want to convolve two lists

of numbers, you treat them like they're coefficients of two polynomials,

you sample those polynomials at enough outputs, multiply those samples point-wise,

and then solve this system to recover the coefficients as a sneaky backdoor way to find

the convolution.

And, as I've stated it so far, at least, some of you could rightfully complain, grant,

that is an idiotic plan, because, for one thing,

just calculating all these samples for one of the polynomials we know already takes

on the order of n-squared operations.

Not to mention, solving that system is certainly going to be

computationally as difficult as just doing the convolution in the first place.

So, like, sure, we have this connection between multiplication and convolutions,

but all of the complexity happens in translating from one viewpoint to the other.

But there is a trick, and those of you who know about Fourier

transforms and the FFT algorithm might see where this is going.

If you're unfamiliar with those topics, what I'm

about to say might seem completely out of the blue.

Just know that there are certain paths you could have

walked in math that make this more of an expected step.

Basically, the idea is that we have a freedom of choice here.

If instead of evaluating at some arbitrary set of inputs, like 0, 1, 2, 3,

on and on, you choose to evaluate on a very specially selected set of complex numbers,

specifically the ones that sit evenly spaced on the unit circle,

what are known as the roots of unity, this gives us a friendlier system.

The basic idea is that by finding a number where taking its powers falls into

this cycling pattern, it means that the system we generate is going to have a

lot of redundancy in the different terms that you're calculating,

and by being clever about how you leverage that redundancy,

you can save yourself a lot of work.

This set of outputs that I've written has a special name.

It's called the discrete Fourier transform of the coefficients,

and if you want to learn more, I actually did another lecture for that same Julia MIT

class all about discrete Fourier transforms, and there's also a really excellent video on

the channel Reducible talking about the fast Fourier transform,

which is an algorithm for computing these more quickly.

Also Veritasium recently did a really good video on FFTs, so you've got lots of options.

And that fast algorithm really is the point for us.

Again, because of all this redundancy, there exists a method to go from

the coefficients to all of these outputs, where instead of doing on

the order of n squared operations, you do on the order of n times the

log of n operations, which is much much better as you scale to big lists.

And, importantly, this FFT algorithm goes both ways.

It also lets you go from the outputs to the coefficients.

So, bringing it all together, let's look back at our algorithm outline.

Now we can say, whenever you're given two long lists of numbers,

and you want to take their convolution, first compute the fast Fourier transform of

each one of them, which, in the back of your mind,

you can just think of as treating them like they're the coefficients of a polynomial,

and evaluating it at a very specially selected set of points.

Then, multiply together the two results that you just got, point-wise,

which is nice and fast, and then do an inverse fast Fourier transform,

and what that gives you is the sneaky backdoor way to compute the convolution that

we were looking for.

But this time, it only involves O of n log n operations.

That's really cool to me.

This very specific context where convolutions show up,

multiplying two polynomials, opens the doors for an algorithm

that's relevant everywhere else where convolutions might come up.

If you want to add probability distributions, do some large image processing,

whatever it might be, and I just think that's such a good example of why you should be

excited when you see some operation or concept in math show up in a lot of seemingly

unrelated areas.

If you want a little homework, here's something that's fun to think about.

Explain why when you multiply two different numbers,

just ordinary multiplication the way we all learn in elementary school,

what you're doing is basically a convolution between the digits of those numbers.

There's some added steps with carries and the like, but the core step is a convolution.

In light of the existence of a fast algorithm,

what that means is if you have two very large integers,

then there exists a way to find their product that's faster than the method we learn

in elementary school, that instead of requiring O of n squared operations,

only requires O of n log n, which doesn't even feel like it should be possible.

The catch is that before this is actually useful in practice,

your numbers would have to be absolutely monstrous.

But still, it's cool that such an algorithm exists.

And next up, we'll turn our attention to the continuous

case with a special focus on probability distributions.