Mechanics of Materials Lecture 01: Introduction and Course Overview

Summary

This course introduces the mechanics of materials, focusing on how materials behave under load. It builds upon statics, emphasizing the importance of equilibrium conditions. The course explores the concepts of stress and strain, highlighting the impact of material properties and loading conditions on structural design. Students will learn to calculate internal reactions, analyze stress distribution, and apply this knowledge to create economical and robust mechanical structures.

Takeaways

• 📚 The course 'Mechanics of Materials', also known as 'Strength of Materials' or 'Mechanics of Deformable Solids', builds upon the foundation of 'Engineering Mechanics' and requires a solid understanding of statics.
• 🔍 The primary focus of the course is to study how materials behave under various loadings, which is essential for designing economically sound and structurally robust buildings and bridges.
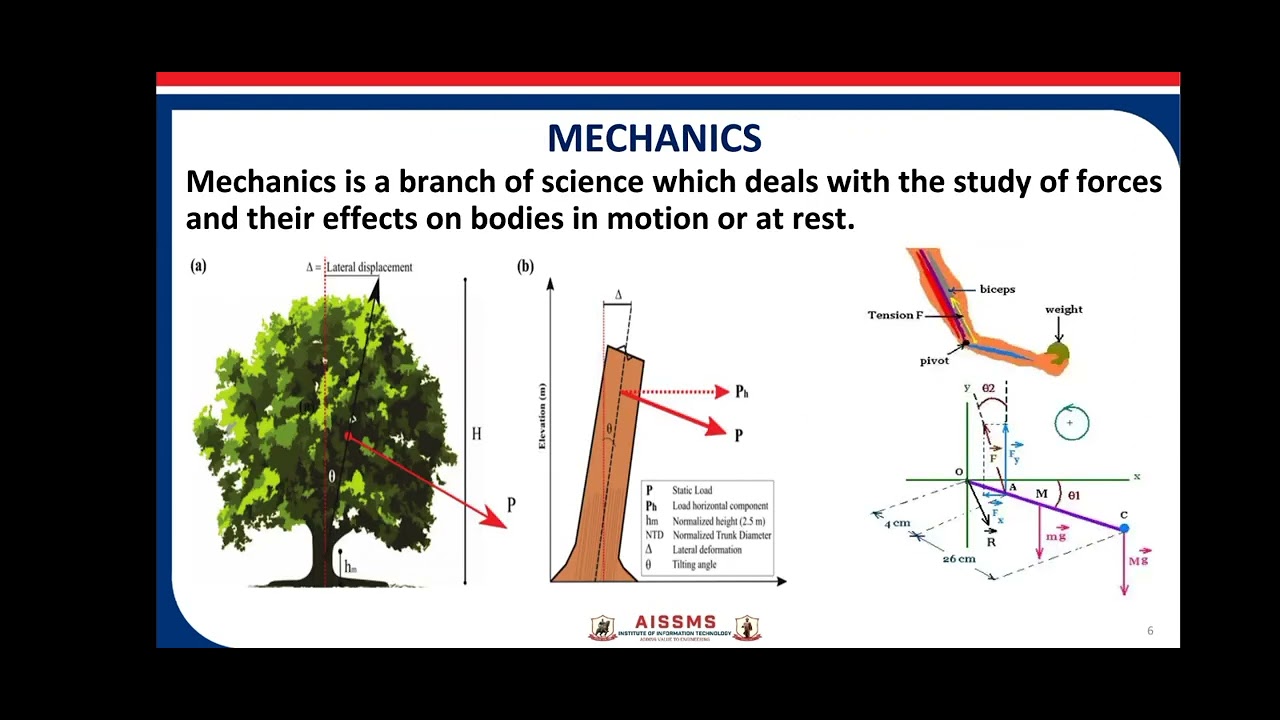
• 🚫 A key distinction from statics is the recognition that materials do deform under load, contrary to the rigid body assumption made in statics.
• 📏 The concept of 'stress' is introduced as a critical factor in material behavior, defined as force per unit area, indicating that the strength of a material is not solely dependent on the magnitude of the load but also on its distribution.
• 🔄 Different types of materials and their mechanical properties lead to different applications, emphasizing the importance of material selection in engineering.
• 🔨 The course explores various scenarios to illustrate the impact of cross-sectional area, direction of load application, and internal reactions on the behavior of materials under stress.
• 📐 The internal reactions in a structure, such as axial force, torsional moment, shear force, and bending moment, result in different stress distributions within the material.
• 📊 Geometric analysis of the cross-sectional area is often necessary to understand how different internal reactions affect the stress distribution within a material.
• 📈 The course covers the determination of the state of stress at a point within a member, including normal and shear stresses, and introduces the concepts of planar and general states of stress.
• 🛠 Students are expected to learn how to quantify material deformation and apply this knowledge to design simple mechanical structures that are both economical and strong.
• 🔮 While the course provides a simplified mathematical model for understanding material behavior, it acknowledges that real-world stress distribution is complex and encourages further study in advanced courses like the theory of elasticity or plasticity.

Q & A

What is the primary focus of the course Mechanics of Materials?

The course Mechanics of Materials, also known as Strength of Materials or Mechanics of Deformable Solids, focuses on understanding how materials behave under loadings and how this knowledge can be applied to design economical and strong structures.

Why is it important to have a foundation in statics before starting the Mechanics of Materials course?

A solid foundation in statics is important because the course continues from the principles of engineering mechanics, and the static equilibrium conditions are still applicable when analyzing the forces and moments acting on a body.

What is the significance of the static equilibrium condition in the context of this course?

The static equilibrium condition is significant because it states that the resultant force vector and the resultant moment vector about any arbitrary point must equal zero, which is a fundamental principle when analyzing structures in equilibrium.

How does the assumption of rigid bodies in statics differ from the reality of material behavior in Mechanics of Materials?

In statics, the assumption is made that objects are rigid bodies that will not deform. However, in Mechanics of Materials, it is acknowledged that real materials do deform, and the course studies the mechanical properties and behavior of materials under loadings.

What is the role of stress in determining the behavior of materials under loading?

Stress, which is force per unit area, plays a crucial role in determining material behavior under loading. It helps to predict whether a material will deform or fail under a given load, and it is a key concept in designing structures.

Why might a thicker shaft be expected to be stronger than a thinner one under the same axial loading?

A thicker shaft is expected to be stronger because it has a larger cross-sectional area, which means it can withstand a higher stress level before failing, as stress is directly related to the force over the area.

What is the difference between normal stress and shear stress?

Normal stress is perpendicular to the surface of a material, causing it to compress or stretch, while shear stress acts parallel to the surface, causing the material to deform or slide along the surface.

How does the orientation of a load affect the type of stress experienced by a material?

The orientation of a load determines whether the material experiences normal stress (from compression or tension) or shear stress (from torsion or bending), which in turn affects how the material deforms or fails.

What is the importance of understanding internal reactions in the study of Mechanics of Materials?

Understanding internal reactions is crucial because they are the forces developed within a member in response to external loadings, and these reactions cause stress distributions that lead to material deformation and potential failure.

What are the four types of internal reactions that can occur in a member?

The four types of internal reactions are normal force (N), axial force along the Y-axis, torsional moment (T), and shear forces (V) along the X and Z axes, along with bending moments (M) that cause normal stress.

How does geometric analysis of a member's cross-sectional area relate to stress calculations?

Geometric analysis is necessary to determine parameters such as area and moment of inertia, which are used in the denominators of stress equations, helping to calculate the stress distribution within a member.

What is the general state of stress at a particle in a member?

The general state of stress at a particle includes six independent stress components: three normal stresses (one along each principal direction) and three shear stresses (one on each pair of orthogonal planes).

How does the orientation of a particle affect the state of stress it experiences?

Changing the orientation of a particle changes the state of stress it experiences, as normal and shear stresses are direction-dependent. This can be analyzed using stress transformation equations.

What are the two main types of deformation that materials can undergo?

Materials can undergo size change (volumetric strain) or shape change (deviatoric strain), which includes simpler deformations like elongation or compression, as well as more complex deformations characterized by an elastic curve.

What is the ultimate goal of studying Mechanics of Materials?

The ultimate goal of studying Mechanics of Materials is to acquire the skills to design simple mechanical structures that are both economical and sufficiently strong to meet the required specifications.