Asinkronus Topik Bentuk Akar W 2

Summary

This educational script introduces the concept of radicals and their relationship with exponents. It explains the conversion between roots and exponents, and how to simplify radical expressions by rationalizing the denominator. The lesson covers basic operations with radicals, such as addition, subtraction, multiplication, and division, emphasizing the importance of having the same index for these operations. It also demonstrates how to simplify complex radical expressions by multiplying by their conjugate to eliminate the radical in the denominator, providing clear examples and encouraging students to practice these concepts.

Takeaways

• 📚 The session focuses on learning about radical expressions, specifically the relationship between exponents and radicals, and how to convert between them.
• 🔢 It's important to understand that for a non-zero real number 'a' and a fraction p/q where q ≠ 0 and q ≥ 2, the equation a^(p/q) = (a^p)^(1/q) holds true, illustrating the conversion between exponents and radicals.
• 👉 The position of the exponent 'p' and the radical 'q' is crucial when converting from one form to another, as it affects the resulting expression.
• 📐 Examples are given to demonstrate the conversion of exponents to radicals and vice versa, such as converting √3 from 7^3 to 7^(1/3).
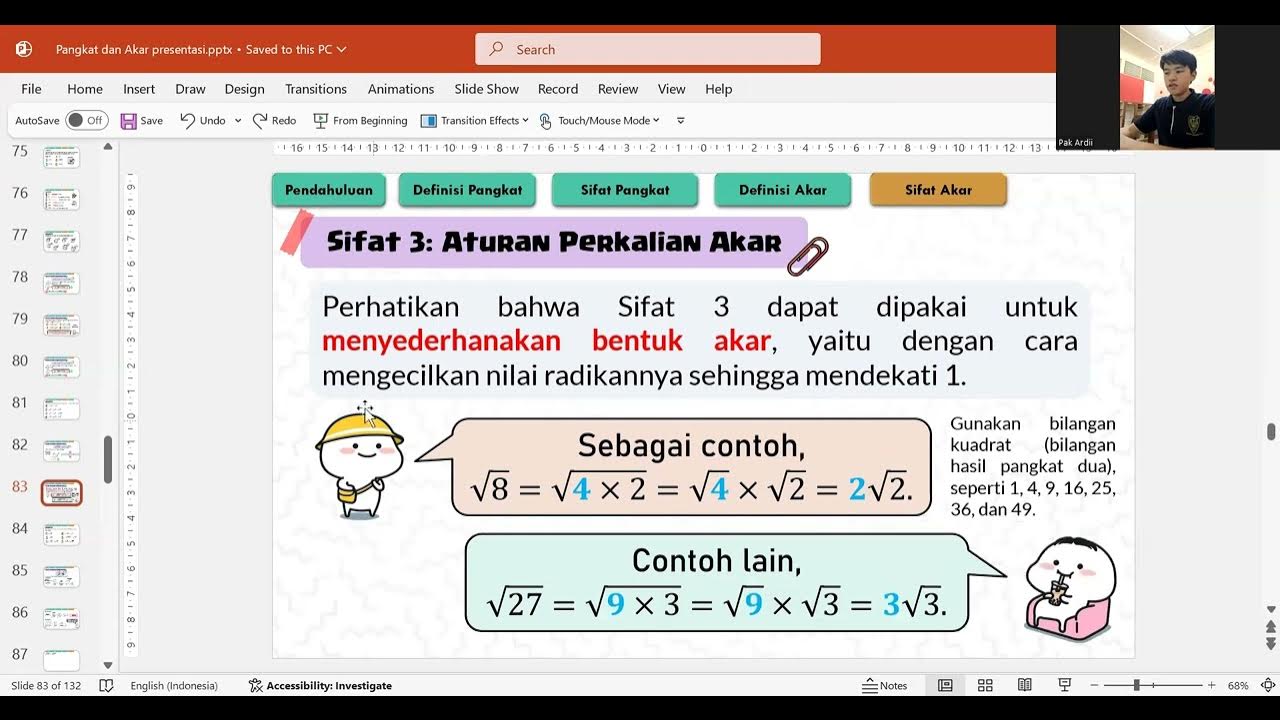
• ➕ Operations on radicals, such as addition and subtraction, are discussed, emphasizing that only like radicals (same index and radicand) can be combined.
• ➖ Similar to addition, subtraction of radicals requires that the radicands and the indices of the radicals be the same.
• 🤔 The script also covers multiplication and division of radicals, where the indices must be the same for these operations to be performed, regardless of the base of the radicals.
• 📉 Rationalizing radicals in the denominator is necessary to simplify expressions and is achieved by multiplying the numerator and denominator by the conjugate of the radical in the denominator.
• 📝 Practice exercises are suggested for students to work on during asynchronous sessions to reinforce their understanding of the concepts taught.
• 📅 The next synchronous session is mentioned, where the exercises will be reviewed, indicating a structured learning process.
• 🙏 The session concludes with a blessing, emphasizing a positive and supportive learning environment.

Q & A

What is the main topic discussed in the script?

The main topic discussed in the script is the relationship between roots and exponents, including the conversion between them, and the operations that can be performed on roots.

What is the condition for the variable 'a' in the script when discussing the relationship between roots and exponents?

The condition for the variable 'a' is that it must be a real number, not equal to 0, and greater than 0.

How is the relationship between roots and exponents expressed mathematically in the script?

The relationship is expressed as \( a^{p/q} = C \), where 'a' is a real number greater than 0, 'p' and 'q' are integers with 'q' not equal to 0 and greater than or equal to 2, and 'C' is the result of the root or exponent operation.

What is the rule for converting from an exponent to a root as mentioned in the script?

The rule for converting from an exponent to a root is \( C = a^{p/q} \) of \( a^{P} \), which becomes \( C = a^{k^q} \) of \( a^P \), where 'P' and 'q' are the positions that change when converting from an exponent to a root.

What are the conditions for adding or subtracting roots as described in the script?

The conditions for adding or subtracting roots are that the roots must have the same radicand and the same index. Only the coefficients (the numbers in front of the roots) are added or subtracted.

Can you provide an example of adding roots from the script?

An example of adding roots from the script is \( 6\sqrt{3} + 2\sqrt{3} \), which simplifies to \( 8\sqrt{3} \) because the coefficients 6 and 2 are added together.

What is the process for multiplying roots as explained in the script?

The process for multiplying roots involves ensuring that the roots have the same index. The bases outside the roots are multiplied together, as well as the numbers inside the roots.

How is division of roots performed according to the script?

Division of roots is performed by ensuring the roots have the same index. The division can be simplified by separating the bases and the numbers inside the roots, and then converting the root to a single base with the same index.

What is the method for rationalizing the denominator of a fraction that contains a root, as described in the script?

The method for rationalizing the denominator involves multiplying the numerator and the denominator by the conjugate of the denominator, which is the same root but with the same base.

Can you give an example of rationalizing the denominator from the script?

An example of rationalizing the denominator from the script is \( \frac{2}{\sqrt{7}} \), which becomes \( \frac{2\sqrt{7}}{7} \) after multiplying both the numerator and the denominator by \( \sqrt{7} \).

What are the signs to watch out for when rationalizing the denominator, especially when dealing with subtraction in the denominator?

When rationalizing the denominator, if there is a subtraction sign in the denominator, the operation changes to addition when multiplying by the conjugate, effectively reversing the operation sign.