Transformaciones lineales y matrices | Esencia del álgebra lineal, capítulo 3
Summary
TLDREl script del video introduce la idea central de las transformaciones lineales y su relación con las matrices en álgebra lineal. Se centra en la visualización de estas transformaciones en dos dimensiones, utilizando la multiplicación de matrices para describir cómo se mueven los vectores bajo una transformación. Se explica que las transformaciones lineales mantienen las líneas rectas y el origen fijo, y se ejemplifican con casos como rotaciones y transformaciones de inclinación. La multiplicación de matrices se presenta como un método para calcular el resultado de una transformación, destacando la importancia de entender las matrices como representaciones de transformaciones espaciales.
Takeaways
- 📚 La idea central del álgebra lineal es la de las transformaciones lineales y su relación con las matrices.
- 🧠 Una transformación lineal es una función que toma un vector y devuelve otro, manteniendo las propiedades de las líneas rectas y el origen fijo.
- 🔍 Para visualizar transformaciones, se sugiere pensar en los vectores como puntos que se mueven en el plano, en lugar de como flechas.
- 📏 Las transformaciones lineales mantienen las líneas de la cuadrícula paralelas y a la misma distancia, incluso después de la transformación.
- 📈 Una transformación lineal se puede describir numéricamente a través de las coordenadas de los vectores de la base tras la transformación.
- 🔢 Las matrices de dos por dos son una forma de representar las transformaciones lineales, donde las columnas representan los vectores de la base tras la transformación.
- 📝 La multiplicación de matrices es una herramienta para calcular el resultado de una transformación lineal aplicada a un vector.
- 🔄 La rotación de 90 grados en el sentido contrario a las agujas del reloj es un ejemplo de transformación lineal que se puede representar con una matriz específica.
- ⏸ La comprensión de las transformaciones lineales es fundamental para entender otros conceptos del álgebra lineal, como la multiplicación de matrices, determinantes y valores propios.
- 🔍 La transformación lineal que comprime el espacio en una línea es un ejemplo de cómo los vectores linealmente dependientes afectan la transformación.
- 📚 Al final del video, se sugiere que el conocimiento de las transformaciones lineales es crucial para entender el álgebra lineal a un nivel más profundo.
Q & A
¿Qué es una transformación lineal y cómo se relaciona con las matrices en álgebra lineal?
-Una transformación lineal es una función que toma un vector y devuelve otro, manteniendo las propiedades de que todas las líneas permanezcan rectas y el origen en su lugar. Se relaciona con las matrices porque una transformación lineal bidimensional se puede describir completamente con solo cuatro números, que son las coordenadas donde terminan los vectores base i y j tras la transformación, y estas se colocan en una matriz de 2x2.
¿Por qué es importante entender las transformaciones lineales en álgebra lineal?
-Es importante porque las transformaciones lineales son fundamentales para entender cómo se transforman los espacios vectoriales. Ayudan a visualizar y calcular el efecto de las operaciones matriciales en los vectores, lo que es esencial para temas avanzados como multiplicación de matrices, determinantes, cambios de base y valores propios.
¿Cómo se visualiza una transformación lineal en dos dimensiones?
-Se visualiza moviendo cada vector de su posición inicial a su posición final. Para facilitar la comprensión, se pueden usar puntos en una cuadrícula infinita, donde se observa cómo se desplazan los puntos bajo la transformación.
¿Cuáles son las propiedades que debe cumplir una transformación para ser lineal?
-Una transformación lineal debe cumplir que todas las líneas rectas se mantengan rectas y el origen debe permanecer en su lugar.
¿Cómo se describe numéricamente una transformación lineal en un programa de animación?
-Se describe utilizando una matriz de 2x2, donde las columnas representan las coordenadas finales de los vectores base i y j tras la transformación. Al multiplicar esta matriz por un vector, se obtiene el vector resultante.
¿Qué es la multiplicación matricial y cómo se relaciona con las transformaciones lineales?
-La multiplicación matricial es el proceso de multiplicar una matriz por un vector, lo que resulta en otro vector. Esta operación se relaciona con las transformaciones lineales porque permite calcular el resultado de aplicar una transformación lineal a un vector.
¿Cómo se describe una rotación de 90 grados en el sentido contrario a las agujas del reloj utilizando una matriz?
-Una rotación de 90 grados en el sentido contrario a las agujas del reloj se describe con la matriz [0, 1; -1, 0]. Al multiplicar esta matriz por un vector, se obtiene el vector resultante de la rotación.
¿Qué sucede con un vector cuando se aplica una transformación que lo deja fijo, como en la inclinada?
-En una transformación donde un vector queda fijo, como en la inclinada, ese vector se considera el eje de la transformación y no cambia su posición. La matriz asociada a esta transformación tendría una columna con el vector fijo y la otra con las nuevas coordenadas del otro vector base tras la transformación.
¿Qué implica que dos vectores sean linealmente dependientes en el contexto de las transformaciones lineales?
-Si dos vectores son linealmente dependientes, significa que uno es una versión escalada del otro, lo que implica que la transformación lineal comprime el espacio en una dimensión, ya que todos los vectores se transforman dentro de una misma línea.
¿Cómo se puede deducir la transformación que se aplica a un vector dado, sin conocer la transformación propiamente dicha?
-Se puede deducir la transformación que se aplica a un vector dado observando las coordenadas finales de los vectores base i y j tras la transformación. A partir de estas, se puede calcular la posición final de cualquier vector utilizando la fórmula de la multiplicación matricial.
¿Cómo se relaciona la idea de las transformaciones lineales con la comprensión de conceptos avanzados en álgebra lineal?
-Las transformaciones lineales son la base para entender conceptos avanzados como la multiplicación de matrices, determinantes, cambios de base y valores propios, ya que todos estos conceptos se relacionan con cómo se transforman los vectores en el espacio.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Transformaciones lineales

¿Qué se estudia en Álgebra Lineal? | MathPures

1 - Álgebra Lineal │ Introducción y Antecedentes Históricos Parte I.

Producto vectorial bajo la luz de las transformaciones lineales | Álgebra lineal, capítulo 8b
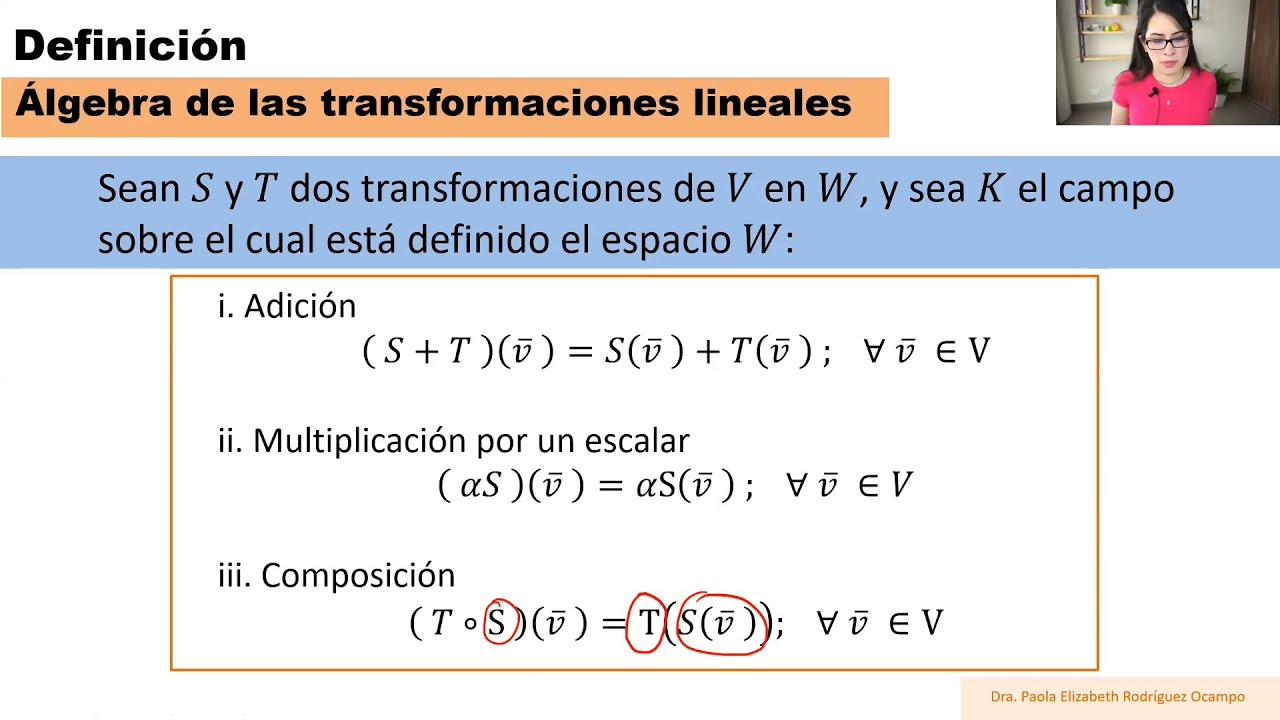
Clase 18 Álgebra Lineal. Transformaciones Lineales - Álgebra de las transformaciones
Vectores en un espacio abstracto | Esencia del álgebra lineal, capítulo 11
5.0 / 5 (0 votes)
