¿Qué se estudia en Álgebra Lineal? | MathPures
Summary
TLDREn este video, se ofrece una introducción al álgebra lineal, centrada en el concepto de espacios vectoriales. Se explica que un espacio vectorial está formado por un conjunto con operaciones de suma y multiplicación por escalar, y se relaciona con campos como los números reales y complejos. El video aborda propiedades fundamentales, subespacios, combinaciones lineales y el concepto de base, que define la dimensión del espacio. También se introduce el tema de las transformaciones lineales y isomorfismos, resaltando la importancia de comprender las estructuras matemáticas y sus interrelaciones, lo que resulta esencial en diversas áreas de las matemáticas.
Takeaways
- 😀 En álgebra lineal, el objeto de estudio son los espacios vectoriales.
- 📦 Un espacio vectorial se define como un conjunto no vacío equipado con dos operaciones binarias y un campo.
- 🔗 Las operaciones en un espacio vectorial son la suma y la multiplicación por escalar.
- ⚖️ Para que un conjunto con estas operaciones sea un espacio vectorial, debe cumplir con propiedades como la conmutatividad y la existencia de un neutro.
- 🔢 Los elementos de un espacio vectorial se llaman vectores, mientras que los elementos del campo se denominan escalares.
- 🌍 Los espacios vectoriales pueden ser reales (con números reales) o complejos (con números complejos), entre otros.
- 🧩 La combinación lineal permite generar vectores a partir de otros vectores en un espacio vectorial.
- 🔍 Un subespacio vectorial es un subconjunto que hereda la estructura del espacio vectorial original.
- 📏 La base de un espacio vectorial es un conjunto de vectores que genera todo el espacio y su cantidad mínima determina la dimensión del espacio.
- 🔄 Las transformaciones lineales permiten establecer relaciones entre diferentes espacios vectoriales, y los espacios isomorfos comparten propiedades esenciales a pesar de ser diferentes.
Q & A
¿Qué es un espacio vectorial?
-Un espacio vectorial es un conjunto de elementos, llamados vectores, que se pueden sumar y multiplicar por escalares, cumpliendo ciertas propiedades específicas.
¿Cuáles son las dos operaciones binarias necesarias para definir un espacio vectorial?
-Las dos operaciones son la suma de vectores y la multiplicación por un escalar.
¿Qué propiedades debe cumplir un espacio vectorial?
-Las propiedades incluyen la conmutatividad y asociatividad de la suma, la existencia del vector cero, la existencia de inversos para la suma, y la compatibilidad de las operaciones.
¿Qué es un campo en el contexto de espacios vectoriales?
-Un campo es un conjunto de números con dos operaciones (suma y producto) que cumplen propiedades similares a las de los números reales.
¿Cuál es la diferencia entre un espacio vectorial real y uno complejo?
-Un espacio vectorial real utiliza el campo de los números reales, mientras que un espacio vectorial complejo utiliza el campo de los números complejos.
¿Qué es un subespacio vectorial?
-Un subespacio vectorial es un subconjunto de un espacio vectorial que también es un espacio vectorial bajo las mismas operaciones restringidas.
¿Cómo se define una combinación lineal?
-Una combinación lineal de un conjunto de vectores es la suma de esos vectores multiplicados por escalares.
¿Qué es una base en un espacio vectorial?
-Una base es un conjunto de vectores que genera el espacio vectorial y cuya cantidad mínima de vectores es igual a la dimensión del espacio.
¿Qué son las transformaciones lineales?
-Las transformaciones lineales son funciones entre espacios vectoriales que preservan las operaciones de suma y multiplicación por un escalar.
¿Qué significa que dos espacios vectoriales son isomorfos?
-Dos espacios vectoriales son isomorfos si hay una transformación lineal entre ellos que es invertible, lo que implica que tienen la misma dimensión y estructura esencial.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Transformaciones lineales | Álgebra lineal

La INCREÍBLE Historia del ÁLGEBRA LINEAL (y sus Matemáticos)

BASE de un ESPACIO VECTORIAL Ejercicios RESUELTOS Álgebra Lineal
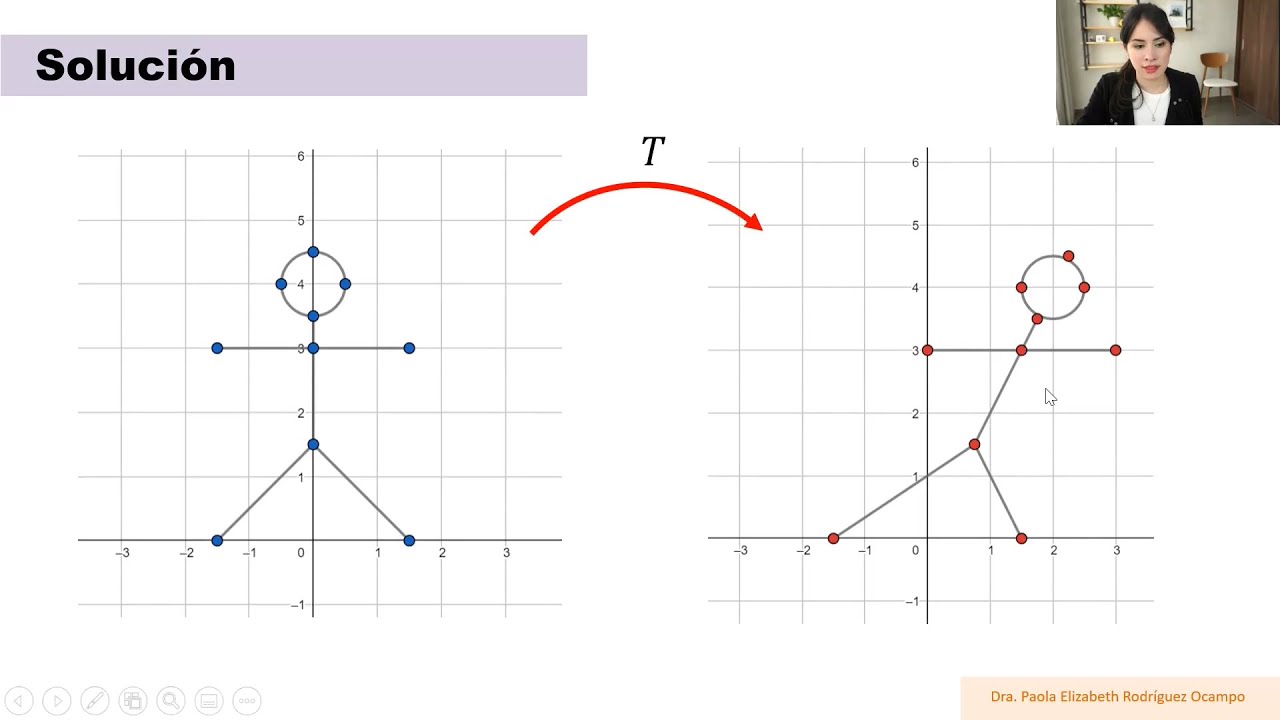
Clase 15 Álgebra Lineal. Transformaciones Lineales - Introducción
Vectores en un espacio abstracto | Esencia del álgebra lineal, capítulo 11

Transformaciones lineales
5.0 / 5 (0 votes)
