Ex 2: Conic Section: Parabola with Vertical Axis and Vertex NOT at the Origin (Down)
Summary
TLDREste video explica cómo graficar una parábola con el vértice en el origen y cómo identificar todas sus características clave. Se abordan aspectos como la forma general de la ecuación, el signo de 'A' que determina si la parábola abre hacia arriba o hacia abajo, y cómo encontrar el foco, la directriz y la longitud del diámetro focal (latus rectum). Además, se enseña cómo usar la geometría de la parábola para entender su simetría y determinar las coordenadas del foco y la ecuación de la directriz, facilitando una representación precisa de la parábola.
Takeaways
- 😀 La ecuación de una parábola con el vértice en el origen tiene la forma 'x^2 = 4ay'.
- 😀 Si el coeficiente 'a' es negativo, la parábola se abre hacia abajo, y si es positivo, hacia arriba.
- 😀 El eje de simetría de la parábola es la línea vertical 'x = 0', es decir, el eje Y.
- 😀 La distancia desde el vértice hasta la directriz es igual al valor absoluto de 'a'.
- 😀 La distancia desde el vértice hasta el foco también es igual al valor absoluto de 'a'.
- 😀 El foco se encuentra dentro de la parábola, y la parábola la envuelve.
- 😀 La ecuación de la directriz es una línea horizontal y se encuentra a 'a' unidades del vértice en la dirección opuesta al foco.
- 😀 El segmento verde llamado 'diámetro focal' o 'latus rectum' tiene una longitud de |4a|, es paralelo a la directriz y pasa por el foco.
- 😀 El valor de 'a' en la ecuación 'x^2 = -3y' es -3/4 o -0.75, lo que significa que la parábola se abre hacia abajo.
- 😀 El foco de la parábola tiene coordenadas (0, -0.75) y la directriz tiene la ecuación y = 0.75.
- 😀 La longitud del latus rectum es de 3 unidades, y sus puntos finales se encuentran a 1.5 unidades a la izquierda y derecha del foco.
Q & A
¿Cuál es la forma general de una parábola con vértice en el origen?
-La forma general es x² = 4ay o y² = 4ax, dependiendo de si la parábola se abre hacia arriba/abajo o hacia la derecha/izquierda. En este caso, x² = 4ay.
¿Cómo se determina si la parábola se abre hacia arriba o hacia abajo?
-Se determina por el signo de 'a'. Si 'a' es positivo, la parábola se abre hacia arriba; si 'a' es negativo, se abre hacia abajo.
¿Cuál es el vértice de la parábola en el ejemplo?
-El vértice está en el origen, es decir, en el punto (0, 0).
¿Qué papel tiene el eje de simetría en una parábola con vértice en el origen?
-El eje de simetría es la línea que divide a la parábola en dos partes iguales. En este caso, es el eje Y, cuya ecuación es x = 0.
¿Cómo se calcula el valor de 'a' a partir de la ecuación x² = -3y?
-Se iguala 4a = -3, y al dividir ambos lados entre 4 se obtiene a = -3/4 o -0.75.
¿Hacia qué dirección se abre la parábola del ejemplo y por qué?
-Se abre hacia abajo porque el valor de 'a' es negativo (-3/4).
¿Cómo se determina la posición del foco y la directriz?
-Ambos se encuentran a una distancia igual al valor absoluto de 'a' desde el vértice. El foco está |a| unidades debajo del vértice y la directriz está |a| unidades por encima.
¿Cuáles son las coordenadas del foco y la ecuación de la directriz en este caso?
-El foco está en (0, -0.75) y la ecuación de la directriz es y = 0.75.
¿Qué es el latus rectum o diámetro focal?
-Es un segmento que pasa por el foco, es paralelo a la directriz y tiene una longitud igual al valor absoluto de 4a.
¿Cuál es la longitud del latus rectum en este ejemplo y cuáles son sus extremos?
-La longitud es 3 unidades, y los extremos son los puntos (-1.5, -0.75) y (1.5, -0.75).
¿Por qué es útil conocer el latus rectum al graficar una parábola?
-Porque ayuda a ubicar puntos adicionales por donde pasa la parábola, permitiendo dibujar una representación más precisa.
¿Qué significa que la parábola sea simétrica respecto al eje Y?
-Significa que si se dobla la gráfica sobre el eje Y, ambos lados coinciden exactamente, mostrando que cada punto tiene un reflejo opuesto en el otro lado del eje.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示
FUNCIÓN CUADRÁTICA - Cómo graficarla calculando todos sus puntos mas importante

Ex 6: Conic Section: Parabola with Horizontal Axis and Vertex NOT at the Origin (Right)

FUNCIÓN CUADRÁTICA: Explicación Completa y Cómo Graficarla

Ecuación de la parábola | Gráfica y ecuación conociendo vértice y foco Ejemplo 1

Funciones Cuadráticas (Definición, propiedades y representación)
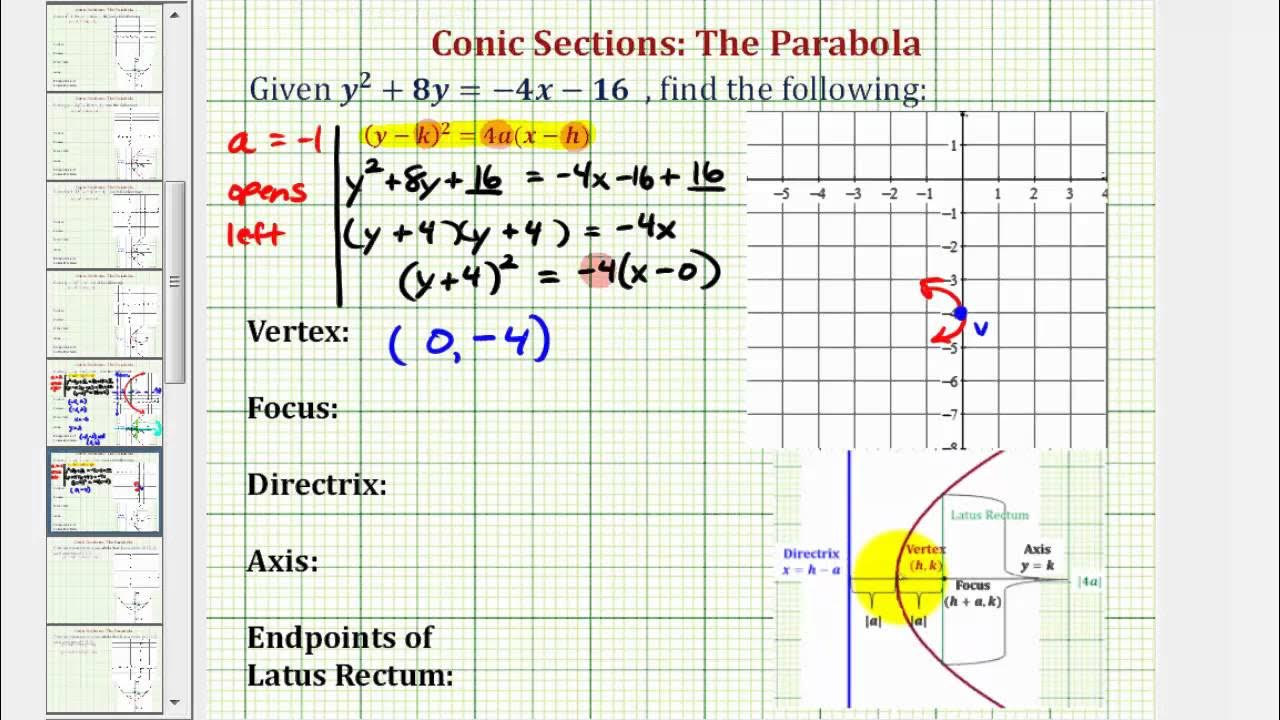
Ex 10: Conic Section: Parabola with Horizontal Axis and Requires Completing the Square (Left)
5.0 / 5 (0 votes)
