Teorema de Pitágoras | Encontrar la hipotenusa
Summary
TLDREn este video, se explica cómo calcular la hipotenusa de un triángulo rectángulo utilizando el teorema de Pitágoras. A través de ejercicios prácticos, el instructor muestra cómo aplicar la fórmula, destacando la relación entre los lados del triángulo: la hipotenusa (el lado más largo) y los catetos. Se enseñan dos ejemplos, uno con valores sencillos y otro más complejo que involucra un cálculo con raíces cuadradas. El video también invita a los espectadores a practicar con ejercicios adicionales, brindando un enfoque accesible y detallado para entender este concepto fundamental de la geometría.
Takeaways
- 😀 El teorema de Pitágoras se aplica solo en triángulos rectángulos, es decir, aquellos que tienen un ángulo recto.
- 😀 Los dos lados que forman el ángulo recto se llaman 'piernas' y son identificados como A y B.
- 😀 El lado opuesto al ángulo recto es la 'hipotenusa', y es el lado más largo del triángulo.
- 😀 La fórmula básica del teorema de Pitágoras es: hipotenusa² = pierna A² + pierna B².
- 😀 Para encontrar la hipotenusa, debemos tomar la raíz cuadrada de la suma de los cuadrados de las piernas.
- 😀 Cuando conocemos las longitudes de las piernas, reemplazamos esos valores en la fórmula para resolver la hipotenusa.
- 😀 Un ejemplo práctico mostró cómo encontrar la hipotenusa de un triángulo con piernas de 3 cm y 4 cm, resultando en 5 cm.
- 😀 Otro ejemplo ilustró un triángulo con piernas de 12 m y 8 m, dando una hipotenusa de 14.42 m tras realizar los cálculos.
- 😀 Si la suma de los cuadrados no tiene una raíz cuadrada exacta, se puede utilizar una calculadora o aproximar la raíz cuadrada.
- 😀 Al final del video, se ofrecen ejercicios para que los estudiantes practiquen la resolución de triángulos y encuentren sus hipotenusas.
- 😀 Se invita a los estudiantes a suscribirse, comentar, compartir y continuar con el curso completo del teorema de Pitágoras disponible en el canal.
Q & A
¿Qué es el teorema de Pitágoras?
-El teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Es decir, h² = a² + b².
¿Cómo se identifican los lados de un triángulo rectángulo?
-En un triángulo rectángulo, los dos lados que forman el ángulo recto se llaman catetos. El lado opuesto al ángulo recto, que es el más largo, se llama hipotenusa.
¿Qué se debe hacer para encontrar la hipotenusa cuando conocemos los catetos?
-Para encontrar la hipotenusa, se debe aplicar el teorema de Pitágoras, reemplazando los valores de los catetos en la fórmula h² = a² + b², y luego despejando la hipotenusa tomando la raíz cuadrada del resultado.
En el primer ejemplo, ¿cómo se calcula la hipotenusa de un triángulo con catetos de 3 cm y 4 cm?
-Primero, aplicamos la fórmula h² = 3² + 4², lo que da 9 + 16 = 25. Luego, tomamos la raíz cuadrada de 25, que es 5. Por lo tanto, la hipotenusa mide 5 cm.
¿Por qué es importante colocar los paréntesis al calcular la hipotenusa?
-Es importante colocar los paréntesis para asegurarse de que tanto los números como las unidades de medida sean elevados al cuadrado. Sin los paréntesis, solo los números serían elevados al cuadrado, no las unidades.
¿Cómo se resuelve el segundo ejemplo con catetos de 12 metros y 8 metros?
-Usamos la fórmula h² = 12² + 8², lo que da 144 + 64 = 208. Luego, tomamos la raíz cuadrada de 208, lo que da aproximadamente 14.42 metros, por lo tanto, la hipotenusa mide 14.42 metros.
¿Qué sucede si el resultado de la suma de los cuadrados no tiene una raíz cuadrada exacta?
-Si el resultado no tiene una raíz cuadrada exacta, se puede utilizar una calculadora para encontrar la raíz cuadrada o aproximarla mentalmente si es posible.
En los ejercicios finales, ¿cuál es el proceso para encontrar la hipotenusa de un triángulo con catetos de 16 cm y 6 cm?
-Aplicamos el teorema de Pitágoras: h² = 16² + 6², lo que da 256 + 36 = 292. Luego, tomamos la raíz cuadrada de 292, lo que da aproximadamente 17.08 cm.
En el último ejercicio, ¿cómo se calcula la hipotenusa de un triángulo con catetos de 4 cm?
-Aplicamos la fórmula h² = 4² + 4², lo que da 16 + 16 = 32. Luego, tomamos la raíz cuadrada de 32, lo que da aproximadamente 5.65 cm.
¿Qué importancia tiene recordar las unidades de medida al aplicar el teorema de Pitágoras?
-Es fundamental recordar las unidades de medida, ya que la raíz cuadrada de las unidades también debe ser tomada en cuenta al calcular la hipotenusa. Esto garantiza que el resultado esté en la misma unidad que los catetos.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

12. Programación en C - Operadores - Ejercicio Hipotenusa de un triángulo rectángulo

Teorema de Pitágoras | Ejercicios programación en C

Distancia entre dos puntos, usando Teorema de Pitágoras
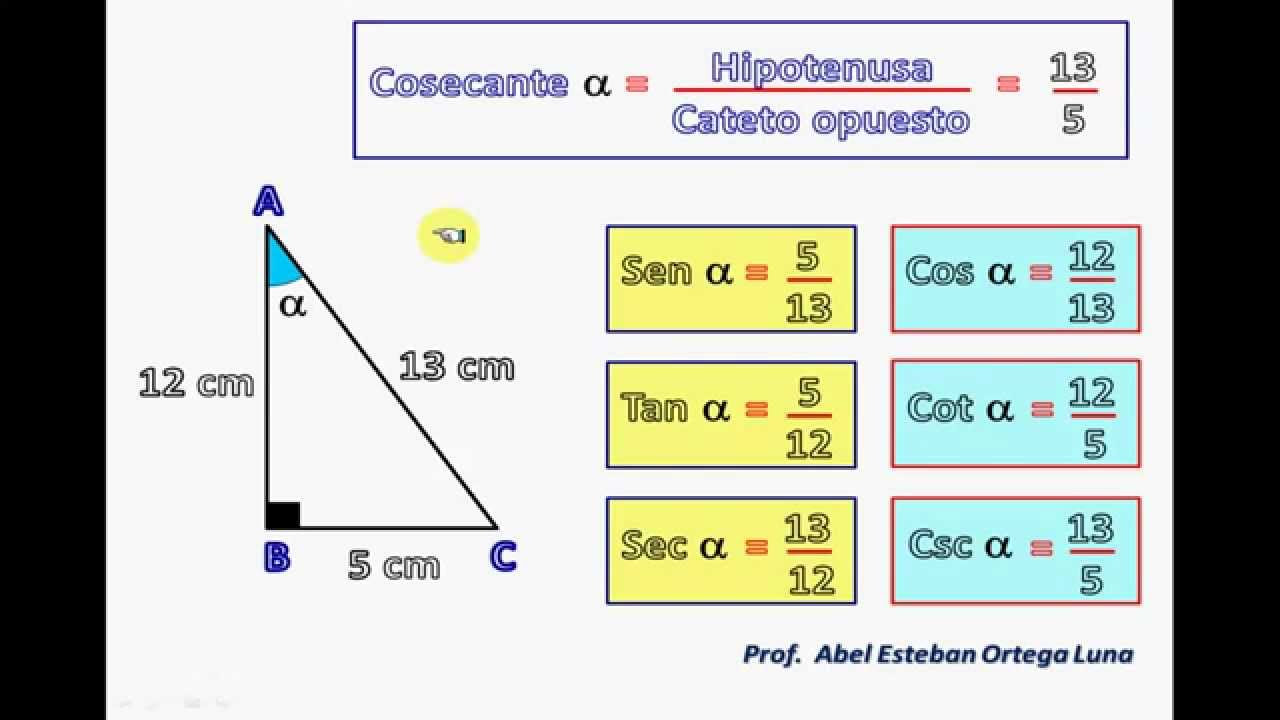
RAZONES TRIGONOMÉTRICAS EN UN TRIÁNGULO RECTÁNGULO

Distancia entre dos puntos ejemplo 3 método gráfico

Solucionar un triángulo rectángulo | Razones trigonométricas | Ejemplo 1
5.0 / 5 (0 votes)
