z score word problems

Summary

The video explains how to calculate probabilities and percentiles using z-scores in the context of IQ and ACT scores. It starts by demonstrating how to calculate the z-score for values lower than 92 and higher than 130, highlighting the use of a standard normal distribution. The video then delves into how to determine the probability of ACT scores below 20, above 31, and between 25 and 32. With detailed examples, it explains how to calculate z-scores, read probability values from the z-table, and apply the results to real-life scenarios.

Takeaways

• 😀 Z-scores are essential for understanding the percentage or probability of certain values in a normal distribution, such as IQ scores.
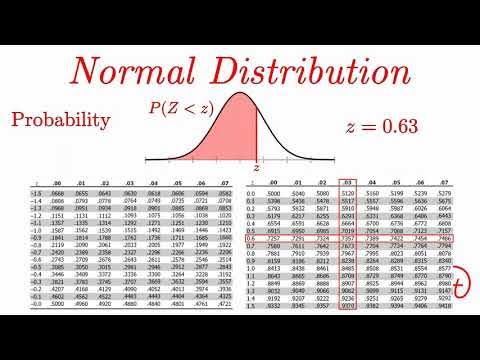
• 😀 To calculate a z-score, the formula is Z = (X - μ) / σ, where X is the value, μ is the mean, and σ is the standard deviation.
• 😀 When calculating the percentage of the population with an IQ below a certain value (like 92), a negative z-score of -0.53 corresponds to about 29.8%.
• 😀 For an IQ score of 130, the z-score is 2.0, which corresponds to about 97.7% of the population having a score lower than 130.
• 😀 Percentages above a certain z-score can be found by subtracting the area to the left from 1 (for example, for a z-score of 2.0, the percentage above it is 2.28%).
• 😀 The ACT scores for students with a GPA of 3.5 to 4.0 were normally distributed with a mean of 24.2 and a standard deviation of 4.2.
• 😀 To calculate the probability that a student's ACT score is below 20, the z-score is -1.0, which gives a probability of 15.87%.
• 😀 For ACT scores greater than 31, the z-score is 1.62, and the probability is 5.26%, meaning only 5% of students score higher than 31.
• 😀 To find the probability of ACT scores between 25 and 32, two z-scores must be calculated: for 25, it is 0.19, and for 32, it is 1.86.
• 😀 The area between two z-scores is found by calculating the probabilities for both z-scores and subtracting the smaller from the larger, which in this case results in a probability of 39.33% for scores between 25 and 32.

Q & A

What is a deviation IQ score, and how is it calculated?

A deviation IQ score is a type of IQ score where the mean is 100 and the standard deviation is 15. It is calculated using the formula: Z = (X - μ) / σ, where X is the raw score, μ is the mean, and σ is the standard deviation.

What does a negative z-score indicate in terms of the normal distribution?

A negative z-score indicates that the data point is below the mean. In a normal distribution, the area to the left of the mean corresponds to values lower than the average.

How do you interpret the z-score of -0.53 in the context of IQ scores?

A z-score of -0.53 means that the IQ score is 0.53 standard deviations below the mean. Referring to the Z-table, this corresponds to about 29.81% of the population having IQs lower than 92.

How do you calculate the percentage of the population with scores above a given value, like 130?

To calculate the percentage of the population with scores above a given value, first calculate the z-score for that value. Then, find the cumulative probability (area under the curve) for that z-score. Subtract this probability from 1 to get the percentage above the given score.

What does the z-score of 2.00 correspond to in the context of IQ scores?

A z-score of 2.00 corresponds to an IQ score of 130. From the Z-table, this z-score corresponds to a cumulative probability of 0.9772, meaning 97.72% of the population has an IQ score below 130.

What is the probability that an ACT score is less than 20, given the mean is 24.2 and the standard deviation is 4.2?

The probability of an ACT score being less than 20 is found by calculating the z-score for 20, which is -1.00. Referring to the Z-table, this gives a probability of 0.1587, or 15.87% of the population scoring below 20.

How is the probability of scores above a certain value calculated using the z-score?

To calculate the probability of scores above a given value, first find the z-score, then look up the cumulative probability for that z-score. Subtract the cumulative probability from 1 to find the area (probability) above the given score.

What is the probability of scoring higher than 31 on the ACT, given the mean is 24.2 and the standard deviation is 4.2?

For an ACT score of 31, the z-score is 1.62. From the Z-table, this corresponds to a cumulative probability of 0.9474, meaning 94.74% of the population scores below 31. Subtracting from 1 gives a probability of 5.26% for scores above 31.

How do you calculate the percentage of the population with scores between two values, like 25 and 32 on the ACT?

To calculate the percentage between two scores, calculate the z-scores for both values. Find the cumulative probabilities for each z-score, then subtract the lower probability from the higher one to find the area (probability) between the two values.

What is the probability that an ACT score is between 25 and 32, given the mean is 24.2 and the standard deviation is 4.2?

For ACT scores between 25 and 32, the z-scores are 0.19 and 1.86, respectively. The cumulative probabilities for these z-scores are 0.5753 and 0.9686. Subtracting these gives a probability of 0.3933, or 39.33% of the population scoring between 25 and 32.