Matematika Kelas 8 Bab 4 - Sudut Luar Segi Banyak - hal. 113 - 114 - Kurikulum Merdeka
Summary
TLDRThis educational video focuses on the properties of polygons, particularly their exterior angles. It covers key concepts such as calculating the sum of exterior angles for different polygons (quadrilaterals, pentagons, hexagons, and octagons) and emphasizes that the sum of exterior angles for any polygon is always 360 degrees. The lesson provides step-by-step examples, demonstrating how to calculate the exterior angle of regular polygons and discusses the rotational symmetry of polygons. The video also explores solving problems related to the number of sides and exterior angles, with a focus on interactive learning and practice.
Takeaways
- 😀 The lesson focuses on investigating the properties of geometric shapes, specifically polygons, and their exterior angles.
- 😀 The sum of the exterior angles of any polygon, regardless of the number of sides, is always 360 degrees.
- 😀 The script demonstrates how to calculate the exterior angles of different polygons, such as quadrilaterals, pentagons, and hexagons.
- 😀 For a quadrilateral, the sum of the exterior angles was found to be 360 degrees, as illustrated through specific examples.
- 😀 The sum of exterior angles in a regular polygon can be determined using the formula: number of sides (n) × 180° − sum of interior angles.
- 😀 The lesson explains that the sum of exterior angles of polygons, regardless of the number of sides, equals 360 degrees due to the rotational symmetry of the shapes.
- 😀 The process of finding the sum of exterior angles of polygons can be simplified by adding together the individual angles at each vertex.
- 😀 The script introduces a method for calculating the sum of exterior angles of polygons with more than four sides, such as pentagons and hexagons, using the same principle.
- 😀 The sum of interior and exterior angles at each vertex always equals 180 degrees, providing a key insight into geometric calculations.
- 😀 An important problem is posed where students are asked to find the sum of exterior angles for an octagon, reinforcing the general rule that the total sum is always 360 degrees.
Q & A
What is the sum of the exterior angles of any polygon?
-The sum of the exterior angles of any polygon is always 360 degrees, regardless of the number of sides.
How do you calculate the exterior angle of a polygon?
-To calculate the exterior angle of a polygon, subtract the interior angle from 180 degrees. For example, if the interior angle is 75 degrees, the exterior angle would be 180 - 75 = 105 degrees.
What is the total sum of the exterior angles for a quadrilateral?
-The sum of the exterior angles of a quadrilateral is 360 degrees. This is true for all polygons, including quadrilaterals.
Why is the sum of the exterior angles of any polygon always 360 degrees?
-This is because the exterior angles are formed by extending the sides of the polygon. When you add up all the exterior angles, they complete a full rotation around the polygon, which is always equal to 360 degrees.
How do you find the sum of the exterior angles for a polygon with 'n' sides?
-The sum of the exterior angles for any polygon, regardless of the number of sides, is always 360 degrees. Therefore, it doesn't depend on the number of sides (n).
What is the process for calculating the sum of exterior angles for a polygon with 5 sides (pentagon)?
-For a pentagon, you calculate the exterior angles for each vertex. Afterward, you sum them up. The sum will always be 360 degrees, as the rule for all polygons.
What is the relationship between the interior and exterior angles of a polygon?
-The interior and exterior angles of a polygon at each vertex always add up to 180 degrees. This is because they form a straight line (a supplementary angle).
How do you calculate the exterior angle of a regular polygon with a known interior angle?
-To find the exterior angle of a regular polygon, subtract the interior angle from 180 degrees. For example, if the interior angle is 120 degrees, the exterior angle would be 180 - 120 = 60 degrees.
In the lesson, what was the calculation for the sum of the exterior angles of a hexagon?
-In the hexagon example, the sum of the exterior angles was calculated as 360 degrees. This is consistent with the rule for any polygon, where the sum of the exterior angles is always 360 degrees.
How is the total exterior angle for a regular polygon with 'n' sides determined?
-The total sum of the exterior angles for any regular polygon is 360 degrees. The individual exterior angle can be found by dividing 360 degrees by the number of sides (n).
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Pembahasan Mari Kita Periksa Garis Sejajar dan Segi Banyak Hal 115 Bab 4 Kelas 8 Kurikulum Merdeka

Matematika Kelas 8 Bab 4 - Sudut Dalam Segi Banyak - hal. 110 - 112 - Kurikulum Merdeka

Interior and Exterior angles of polygons
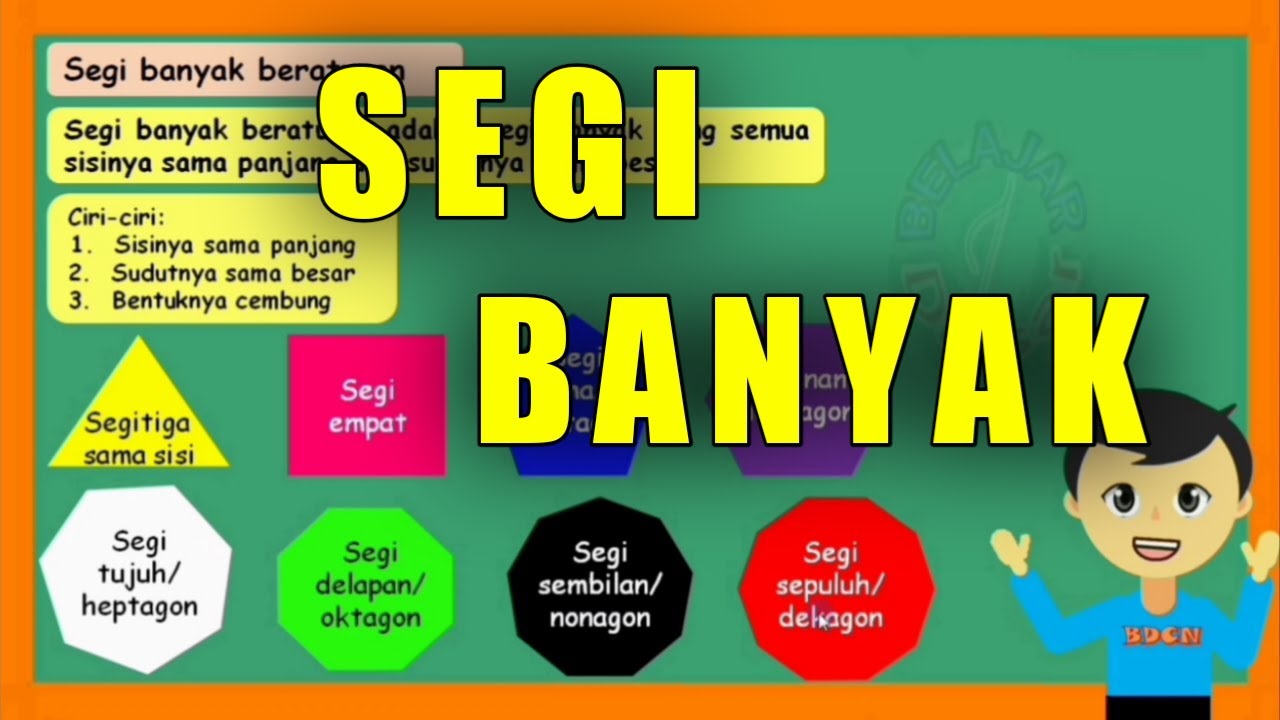
Segi Banyak | Matematika Kelas 4 SD

Angles in Polygons

#23 Angles in Polygons - Series 2 Edexcel IGCSE Exam Questions
5.0 / 5 (0 votes)
