Regla de Simpson. Aproximación de integrales. Ejemplo 1
Summary
TLDREn este video tutorial, Jesús Grajeda muestra cómo resolver una integral utilizando la Regla de Simpson, una técnica de aproximación para calcular áreas bajo la curva de una función. Jesús explica que la integral no se puede resolver de manera directa ni con sustituciones comunes, y por ello, se requiere un método de aproximación. A través de una gráfica y un paso a paso detallado, Jesús guía al espectador en el proceso de calcular el área utilizando la fórmula de Simpson, incluyendo la elección del número de rectángulos y la evaluación de la función en puntos clave. Finalmente, compara el resultado aproximado con el valor exacto obtenido mediante una calculadora, demostrando la precisión de la aproximación.
Takeaways
- 😀 Jesús Grajeda presenta un nuevo video tutorial sobre cómo resolver una integral utilizando la Regla de Simpson.
- 📚 La integral mostrada en el video no puede ser resuelta de manera directa ni con métodos de sustitución, por partes o fracciones parciales, ni con sustitución trigonométrica.
- 📉 La Regla de Simpson es un método de aproximación para calcular integrales, y el video explica cómo aplicarla paso a paso.
- 🔢 La fórmula de la Regla de Simpson se presenta en detalle, con una explicación de los coeficientes y cómo se aplican a los valores de la función evaluada en puntos específicos.
- 📈 Se ilustra la Regla de Simpson con una gráfica que muestra cómo se aproxima la curva de la función con rectángulos y parábolas.
- 📝 El video detalla el proceso de calcular el área bajo la curva de una integral definida, utilizando la fórmula de Simpson.
- 📐 Se menciona que 'n' debe ser un número par para aplicar la Regla de Simpson, y se selecciona n=10 como ejemplo.
- 🔢 El cálculo de 'delta de x' se muestra como un paso importante para determinar los valores incrementales de 'x'.
- 📊 Se realiza un ejemplo práctico de cálculo, donde se sustituyen los valores de la función evaluada en puntos 'x0' a 'xn' en la fórmula de Simpson.
- 🤔 Se recomienda realizar la suma de los términos dentro de la fórmula antes de multiplicar por 'delta de x' para evitar errores en la calculadora.
- 📊 Al final del video, se compara el resultado aproximado de la integral utilizando la Regla de Simpson con el resultado obtenido directamente por la calculadora, mostrando una buena concordancia.
Q & A
¿Quién es el presentador del video y qué tema trata?
-El presentador del video es Jesús Grajeda y trata sobre cómo resolver una integral utilizando la regla de Simpson.
¿Por qué no se pueden utilizar métodos tradicionales para resolver la integral mostrada en el video?
-No se pueden utilizar métodos tradicionales como la integración directa, sustitución, método de partes o fracciones parciales trigonométricas porque la integral no se ajusta a esas técnicas.
¿Qué es la regla de Simpson y para qué se usa?
-La regla de Simpson es un método numérico para aproximar el valor de una integral definida. Se usa para calcular el área bajo la curva de una función en un intervalo dado cuando no se puede integrar analíticamente.
¿Cuál es la fórmula básica de la regla de Simpson mencionada en el video?
-La fórmula básica de la regla de Simpson es ∫(a a b) f(x) dx = (Δx/3) * [f(x0) + 4f(x1) + 2f(x2) + ... + 4f(x_{n-1}) + f(xn)] donde Δx = (b - a)/n y n es el número de subintervalos.
¿Cómo se representa gráficamente la aproximación de la regla de Simpson?
-Se representa gráficamente trazar rectángulos y parábolas para aproximar el área bajo la curva de la función. La regla de Simpson usa parábolas para cerrar los rectángulos en lugar de las curvas de la función.
¿Cuántos rectángulos se trazan en el ejemplo dado en el video?
-En el ejemplo dado en el video, se trazan 8 rectángulos para aproximar el área bajo la curva.
¿Cómo se calcula Δx en la regla de Simpson según el video?
-Δx se calcula como (b - a)/n, donde b es el límite superior, a es el límite inferior y n es el número de rectángulos o subintervalos.
¿Cuál es el número de subintervalos (n) que se elige para el ejemplo en el video?
-Para el ejemplo en el video, se elige n = 10 subintervalos para aplicar la regla de Simpson.
¿Cómo se evalúa la integral utilizando la regla de Simpson en el ejemplo del video?
-Se evalúa sustituyendo los valores de x (x0 a x8) y las funciones correspondientes en la fórmula de la regla de Simpson y realizando las operaciones matemáticas necesarias para obtener el resultado aproximado.
¿Cuál es el resultado aproximado de la integral mostrada en el video utilizando la regla de Simpson?
-El resultado aproximado de la integral utilizando la regla de Simpson en el video es 1.4626.
¿Cómo se compara el resultado de la regla de Simpson con el resultado de una calculadora en el video?
-Se compara integrando la función dada (f(x) = x^2) en un intervalo de 0 a 1 utilizando una calculadora, obteniendo el mismo resultado de 1.4626 que con la regla de Simpson, lo que valida la aproximación.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Resolver una Suma de Riemann paso a paso. #MateYisus

Estimar el área bajo una curva usando rectángulos | Comprobando con calculadora
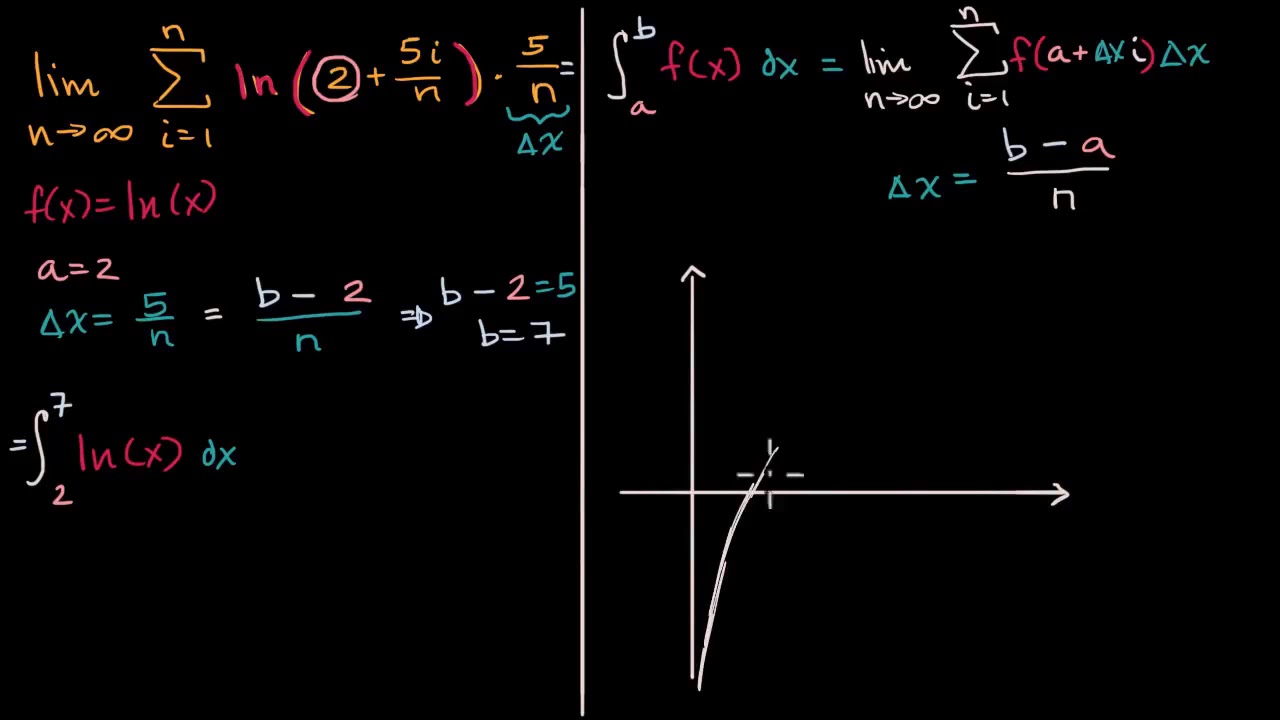
Escribir el límite de una suma de Riemann como una integral definida | Khan Academy en Español

Cuadratura de Gauss parte 1

Sumas de Riemann de punto medio | Khan Academy en Español

Cálculo Integral - Tutorial de Área bajo la curva
5.0 / 5 (0 votes)
