Garis Singgung Lingkaran (2) - Garis Singgung Persekutuan Luar dan Dalam - Matematika SMP
Summary
TLDRIn this educational video, the presenter explains how to calculate the external (GSPL) and internal (GSPD) tangents between two circles. Through clear explanations and step-by-step examples, viewers learn how to apply formulas to determine tangent lengths based on the distance between circle centers and their radii. The video also emphasizes recognizing different tangent types based on the relationship between the circles. With practical exercises and tips, the content helps viewers build confidence in solving geometric problems related to tangents. It's a valuable resource for anyone studying geometry or preparing for exams.
Takeaways
- 😀 External Tangent Lines (GSPL) are lines that touch two circles from the outside, while Internal Tangent Lines (GSPD) touch the circles from between them.
- 😀 The formula for calculating the length of the external tangent (GSPL) is: √(d² - (R₁ - R₂)²), where d is the distance between the centers of the circles and R₁, R₂ are their radii.
- 😀 The formula for calculating the length of the internal tangent (GSPD) is: √(d² - (R₁ + R₂)²).
- 😀 Tangent lines are crucial in geometry and are used to analyze the relationship between two circles, whether they are separate, overlapping, or tangent to each other.
- 😀 Using the Pythagorean theorem, we can derive the formulas for tangent lines by applying the properties of right triangles formed by the circle centers and the points of tangency.
- 😀 When solving problems involving tangents, it is important to correctly identify whether the tangent is external or internal based on the relationship between the circles.
- 😀 In some cases, the distance between the centers (d) or the radii (R₁, R₂) may be unknown. These values can be determined using algebraic equations and known formulas.
- 😀 The distance between the centers of two circles, d, helps in determining the number of tangent lines possible: 2 external and 2 internal when circles are separate, 2 external and 1 internal when externally tangent, and 2 external only when overlapping.
- 😀 Some problems may involve reversing the typical question by giving the length of the tangent line and asking for the radius or distance between the centers.
- 😀 Understanding the geometric relationship between two circles and the different types of tangents (external, internal) is fundamental in solving circle-related problems in mathematics.
Q & A
What is the main topic of the video?
-The main topic of the video is about the tangent lines to circles, specifically focusing on the two types of common tangents for two circles: external and internal tangents.
What is the formula for calculating the length of the external tangent (GSPL)?
-The formula for calculating the external tangent (GSPL) is √(d² - (R - r)²), where d is the distance between the centers of the two circles, R is the radius of the larger circle, and r is the radius of the smaller circle.
How is the formula for the internal tangent (GSPD) different from the external tangent formula?
-The formula for the internal tangent (GSPD) is similar to the external tangent, but instead of subtracting the radii, it adds them: √(d² - (R + r)²).
What is the significance of the Pythagorean Theorem in the calculation of tangents?
-The Pythagorean Theorem is used to derive the formulas for both external and internal tangents, as it relates to the right-angled triangle formed by the centers of the circles and the tangent line.
What does the letter 'd' represent in the tangent formulas?
-'d' represents the distance between the centers of the two circles.
What does the letter 'R' represent in the tangent formulas?
-'R' represents the radius of the larger circle.
What is the geometric relationship between the circles when the tangent is external?
-When the tangent is external, the tangent line touches both circles at a single point on the outer side, and the two circles do not overlap.
What condition must be satisfied for two circles to have two common external tangents?
-The distance between the centers of the circles must be greater than the sum of their radii (d > R + r) for two common external tangents to exist.
How do you calculate the distance between the centers of two circles if given the lengths of the tangents?
-The distance between the centers can be found by rearranging the tangent formulas. For example, if given the length of the external tangent, you can solve for 'd' using the formula d = √(GSPL² + (R - r)²).
How do you handle problems where the tangent length is already provided, and you need to find other parameters such as the radius or the distance between centers?
-In such problems, you can use the provided tangent length to form equations based on the tangent formulas. By manipulating these equations algebraically, you can solve for the unknown parameters like the radius or the distance between centers.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Garis Singgung Lingkaran(2) - Garis Singgung Persekutuan Luar dan Dalam | Matematika Kelas 8 SMP MTs
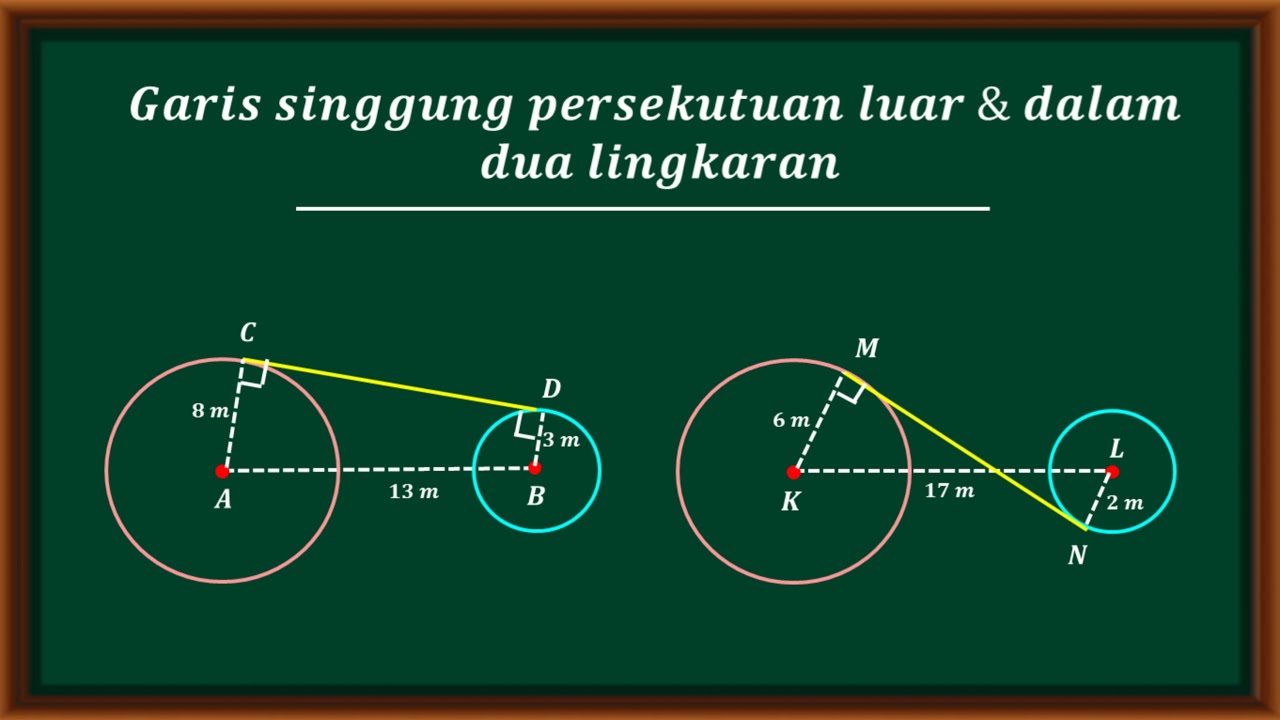
Garis singgung persekutuan luar dan garis singgung persekutuan dalam dua lingkaran

Garis Singgung Persekutuan Dalam dan Luar #garissinggunglingkaran #matematika

Materi Matematika Kelas 8: Lingkaran

Garis Singgung Lingkaran | Matematika SMA Kelas XI

2nd Quarter Grade 10 Math -( Lesson 5) Illustrating Secant, Tangent, Sector and Segment of a Circle
5.0 / 5 (0 votes)
