Mediatriz e Bissetriz

Summary

This video provides a detailed explanation of two important geometric concepts: the mediatriz (perpendicular bisector) and the bissetriz (angle bisector). The mediatriz divides a segment into two equal parts and has the property that any point on it is equidistant from the segment's endpoints. The bissetriz divides an angle into two equal parts, with points on it maintaining equal distances from the angle's rays. The video also covers practical applications like solving equations involving segment lengths and angles, and guides viewers through constructing both figures with compass and straightedge.

Takeaways

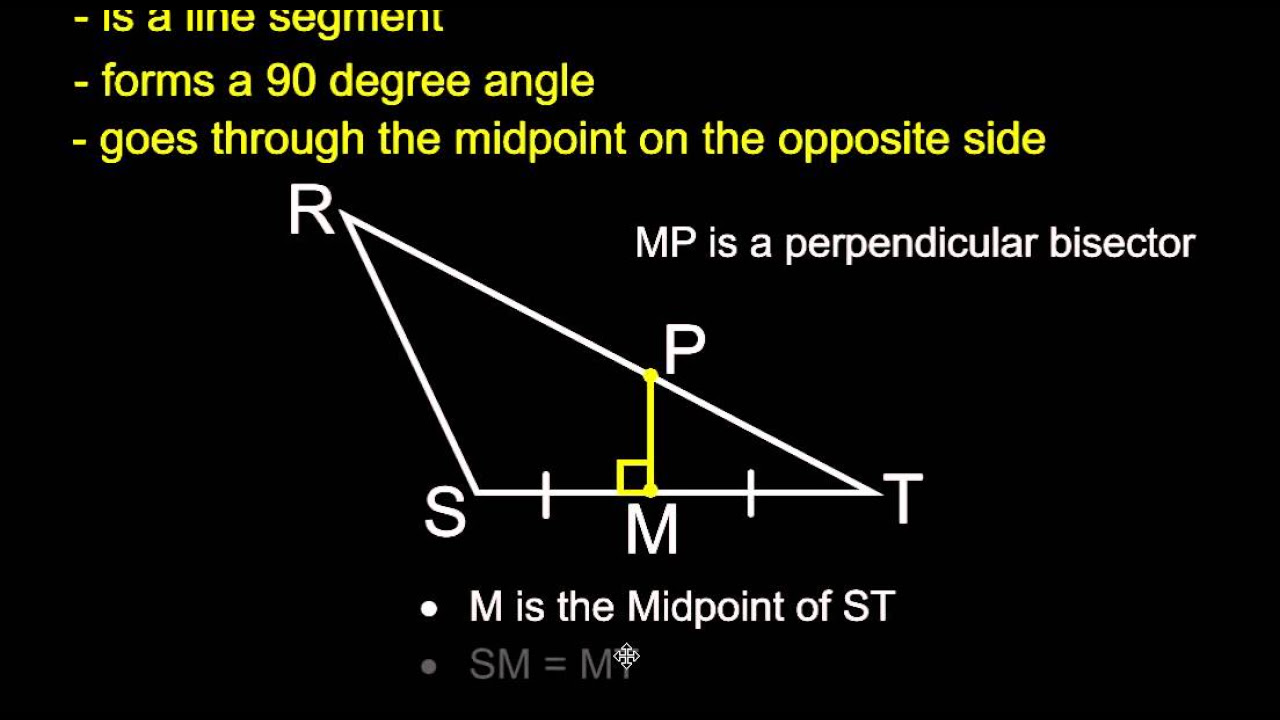
• 😀 The *mediatriz* (perpendicular bisector) is a line that divides a segment into two equal parts at a right angle, passing through the midpoint of the segment.
• 😀 The distances from any point on the *mediatriz* to the endpoints of the segment are always equal.
• 😀 A common exercise involves solving for the unknown in an equation representing the equality of the two parts of a segment divided by the *mediatriz*.
• 😀 The *bissetriz* (angle bisector) divides an angle into two equal parts, creating two smaller angles of the same measure.
• 😀 The distances from any point on the *bissetriz* to the two rays of the angle are always equal.
• 😀 Using the *bissetriz*, you can create inscribed circles within an angle, where the circle touches the two rays forming the angle.
• 😀 The *bissetriz* is used to find the *incenter* of a triangle, the center of an inscribed circle within the triangle.
• 😀 To solve problems with the *bissetriz*, one can use angle relationships, such as the fact that the sum of the angles in a triangle equals 180°.
• 😀 The construction of the *mediatriz* involves using a compass to draw arcs from both ends of the segment, then connecting the points where the arcs intersect.
• 😀 The construction of the *bissetriz* involves using a compass to draw arcs from the vertex of the angle, then connecting the points of intersection to create the bisector.

Q & A

What is a mediatriz (perpendicular bisector) in geometry?

A mediatriz is a line that is perpendicular to a segment and passes through its midpoint, effectively dividing the segment into two equal parts. The angle between the segment and the mediatriz is 90 degrees.

What are the key properties of a mediatriz?

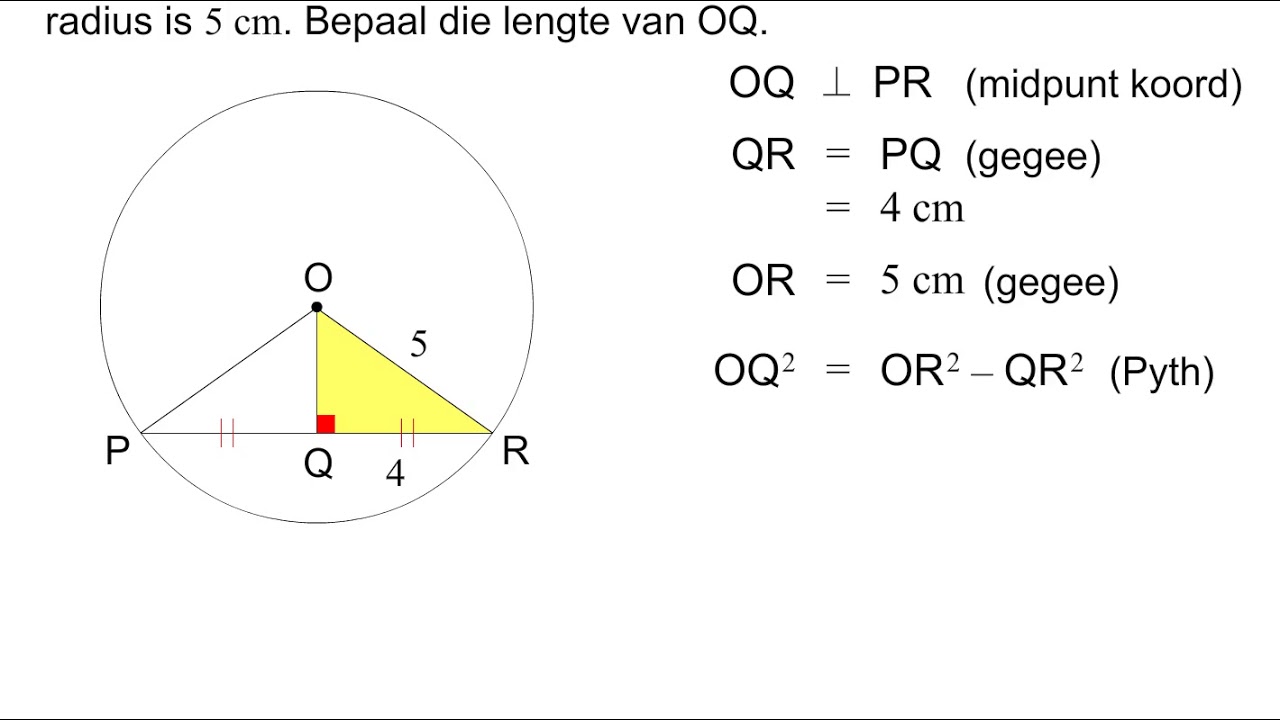
The key properties of a mediatriz include: 1) The distance from any point on the mediatriz to the endpoints of the segment is the same; 2) The segment is divided into two equal parts, with each part having the same length.

How is an equation used to solve problems involving a mediatriz?

Equations often appear in problems involving a mediatriz when comparing the lengths of the two parts of a segment. For instance, an equation might set the lengths of two parts equal to each other, such as 2x + 5 = 14 - x, which can be solved to find the unknown length.

What is a bissetriz (angle bisector) and how does it work?

A bissetriz is a line that divides an angle into two equal smaller angles. It cuts the angle precisely in half, ensuring that the two resulting angles have the same measure.

What are the properties of an angle bisector?

The key property of an angle bisector is that it ensures the distances from any point on the bisector to the two sides of the angle are the same. This property is important when working with inscribed circles or solving related geometric problems.

What is the significance of the angle bisector in geometric constructions?

The angle bisector is used to create equal angles, which is crucial for constructing inscribed circles within angles. It also plays a role in finding the incenter of a triangle, which is the center of a circle inscribed in the triangle.

How is the incenter of a triangle related to the angle bisector?

The incenter of a triangle is the point where the angle bisectors of all three angles of the triangle intersect. This point serves as the center of the incircle, which is the largest circle that can fit inside the triangle, touching all three sides.

What is the method for constructing a mediatriz using a compass and straightedge?

To construct a mediatriz, first find the midpoint of a segment using a compass to draw arcs from each endpoint. Then, connect the two intersection points of the arcs with a straightedge, creating a perpendicular bisector that divides the segment into two equal parts.

What is the method for constructing a bissetriz of an angle?

To construct a bissetriz, place the compass at the angle's vertex, draw an arc that crosses both rays of the angle. Then, using the same compass width, draw arcs from the two intersection points. Finally, connect the intersection of these arcs with a straightedge to create the angle bisector.

How are the properties of the mediatriz and bissetriz applied in solving geometric problems?

The properties of the mediatriz are applied in problems that involve dividing segments into equal parts or calculating distances. The bissetriz is used in problems that require dividing an angle into equal parts or finding the distances from a point to the sides of the angle, especially in triangle-related problems or when dealing with inscribed circles.