LECTURE NOTES: AIRCRAFT AERODYNAMICS I, CHAPTER I, PART 4
Summary
TLDRThis video explores the fundamental process of solving the Navier-Stokes equations for fluid flow analysis. It covers exact solutions, classifications based on flow types and geometries, and the six essential steps involved in solving these equations. Through a step-by-step breakdown, the video illustrates how boundary conditions such as no-slip and interface conditions play a crucial role in determining the uniqueness of the solution. The practical example of steady, laminar flow between parallel plates helps to demonstrate the integration of assumptions, simplifications, and boundary conditions to arrive at an exact solution.
Takeaways
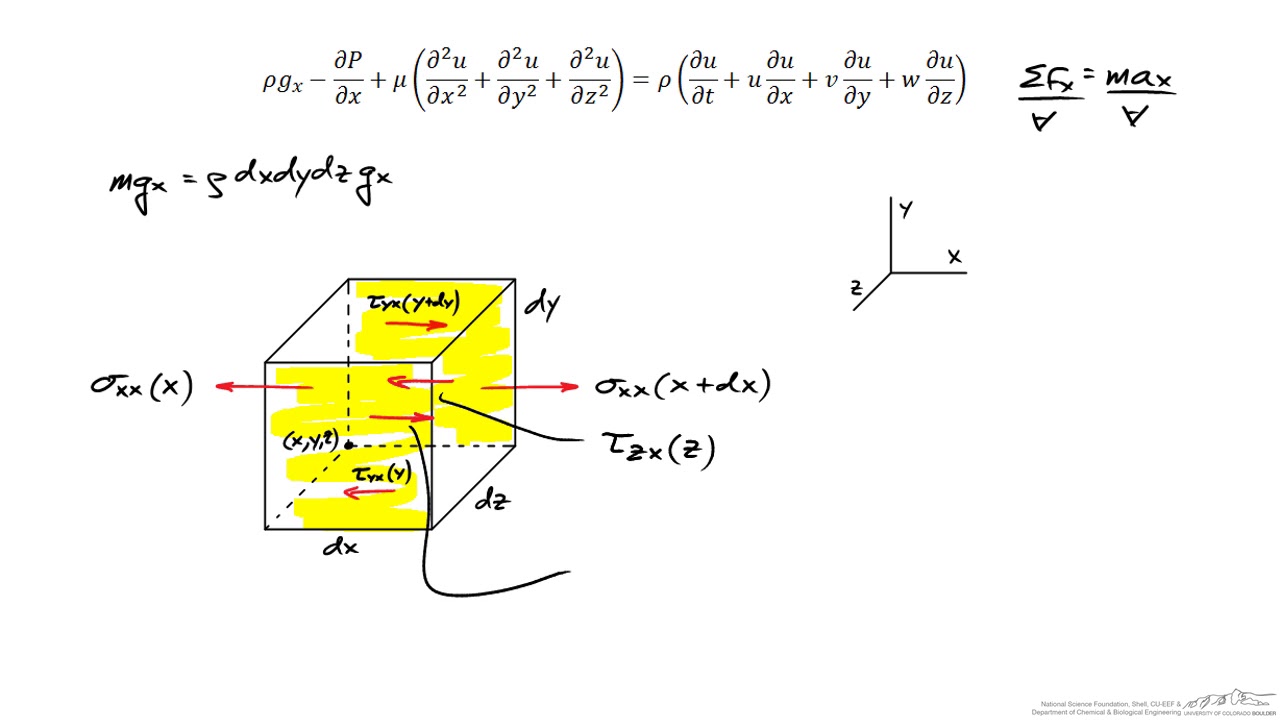
- 😀 The Navier-Stokes equation has around 80 known exact solutions, which are classified based on the convective term in the equation.
- 😀 Solutions to the Navier-Stokes equation can be categorized based on the flow geometry, such as shear flow, steady/unsteady flow, and flow in channels or pipes.
- 😀 There are six basic steps to solve the Navier-Stokes equation: 1) defining the case and geometry, 2) writing assumptions and boundary conditions, 3) simplifying the equations, 4) integrating, 5) applying boundary conditions, and 6) verifying the results.
- 😀 Boundary conditions are critical in obtaining a unique solution to the Navier-Stokes equation and can involve conditions like no-slip, interface, or others depending on the case.
- 😀 The no-slip condition is a common boundary condition, stating that the fluid velocity at a solid surface equals the velocity of the surface itself.
- 😀 Interface boundary conditions apply when two fluids meet, ensuring equal velocity at the boundary and equal shear stress between the fluids.
- 😀 Solving for exact solutions often requires simplifying the governing differential equations, like assuming steady, incompressible, and laminar flow.
- 😀 In the case of two parallel plates with shear flow, conditions such as no pressure gradient, constant gravity, and incompressible, Newtonian fluid are assumed.
- 😀 The solution process involves integrating the simplified equations and applying boundary conditions to obtain velocity and pressure distributions.
- 😀 Verifying the solution is essential; this is done by checking if the obtained velocity and pressure satisfy the original equations and boundary conditions.
- 😀 The shear stress on the lower plate can be computed by substituting the velocity into the stress tensor, leading to the shear stress being proportional to the fluid's viscosity and strain rate.
Q & A
What are the key classifications for the exact solutions of the Navier-Stokes equations?
-Exact solutions to the Navier-Stokes equations are classified based on the convective term (linear or nonlinear) and the type of flow geometry (e.g., steady or unsteady flow, shear flow, and flow in pipes or channels).
What are the six basic steps involved in solving the Navier-Stokes equations?
-The six basic steps are: 1) Define the case and geometry, 2) Write assumptions and boundary conditions, 3) Simplify the governing equations, 4) Integrate the equations, 5) Apply boundary conditions to find integration constants, 6) Verify the solution.
How are boundary conditions used in solving the Navier-Stokes equations?
-Boundary conditions help define the behavior of the fluid at solid boundaries and interfaces. They determine the uniqueness of the solution and are essential in computing the velocity and pressure profiles of the fluid.
What is the no-slip condition, and why is it important in fluid dynamics?
-The no-slip condition states that the velocity of fluid at a solid boundary is equal to the velocity of the boundary itself. It is crucial because it defines how fluid interacts with solid surfaces, ensuring realistic flow behavior near boundaries.
What is the significance of interface conditions between two fluids?
-Interface conditions ensure that the velocity of both fluids at the boundary is the same and that shear stress is equally distributed. This is important for accurately modeling flows involving multiple fluid phases.
What assumptions are made in the example of flow between two parallel plates?
-The assumptions include steady, incompressible, laminar flow; no pressure gradients in certain directions; and gravity acting only in the vertical direction. The flow is also assumed to be two-dimensional in the x and y directions.
How does the simplification of the differential equations affect the solution process?
-Simplifying the differential equations makes the problem more manageable and solvable analytically. By reducing the complexity, the solution can be derived more easily, leading to a clear velocity profile and shear force calculation.
What role does the integration of the simplified equations play in obtaining the solution?
-Integration of the simplified equations provides the general solution for velocity and pressure fields. This step is crucial for obtaining the functional forms of the flow variables before applying boundary conditions.
Why is verifying the solution important after solving the Navier-Stokes equations?
-Verification ensures that the derived solutions satisfy both the differential equations and the boundary conditions. It guarantees the accuracy and consistency of the solution in the given physical context.
In the problem of flow between two plates, how is the shear force calculated?
-The shear force is calculated by substituting the velocity profile into the stress tensor and solving for the shear stress at the lower plate. The shear force per unit area is then determined using the fluid's viscosity and the velocity gradient.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示
5.0 / 5 (0 votes)