Mass defect and binding energy | Nuclear chemistry | Chemistry | Khan Academy
Summary
TLDRThis video explains how to calculate the mass defect and nuclear binding energy of a helium-4 nucleus. It details the process of determining the mass of the nucleus by adding the masses of protons and neutrons, then calculates the mass defect by comparing the predicted and actual mass. Using Einstein’s equation, the energy corresponding to the mass defect is computed, which is the nuclear binding energy. The video concludes by explaining the role of the nuclear strong force in holding the nucleus together despite the repulsion between protons.
Takeaways
- 😀 The helium-4 nucleus consists of 2 protons and 2 neutrons, determined from its atomic number (2) and mass number (4).
- 😀 The predicted mass of a helium-4 nucleus is calculated by adding the mass of two protons and two neutrons in atomic mass units (AMUs).
- 😀 The mass of a proton is approximately 1.00727647 AMUs, and the mass of a neutron is 1.00866490 AMUs.
- 😀 The actual mass of a helium-4 nucleus is measured as 4.00150608 AMUs, which is less than the predicted mass.
- 😀 The difference between the predicted and actual mass is called the mass defect, which is 0.03037666 AMUs.
- 😀 The mass defect represents the mass lost when the nucleus is formed, and it is converted into energy according to Einstein's equation, E = mc².
- 😀 The conversion factor from AMUs to kilograms is 1 AMU = 1.66054 × 10⁻²⁷ kg.
- 😀 The energy released during the formation of the helium-4 nucleus can be calculated by multiplying the mass defect in kilograms by the square of the speed of light.
- 😀 The calculated energy released is approximately 4.53346 × 10⁻¹² Joules.
- 😀 The energy released during nuclear formation is called nuclear binding energy, which is also the energy required to break apart the nucleus into its individual components.
- 😀 The strong nuclear force is responsible for holding the nucleus together, overcoming the repulsive force between positively charged protons.
Q & A
What is the atomic number of helium-4, and how does it relate to the number of protons in the nucleus?
-The atomic number of helium-4 is 2, which means that the helium-4 nucleus contains two protons.
How do you determine the number of neutrons in a helium-4 nucleus?
-To find the number of neutrons in a helium-4 nucleus, subtract the atomic number (2) from the mass number (4). This gives 2 neutrons in the nucleus.
What is the mass of a proton in atomic mass units (amus), and how does this relate to the mass of the helium-4 nucleus?
-The mass of a proton is 1.00727647 amus. For two protons, the total mass is 2.01455294 amus, which contributes to the total mass of the helium-4 nucleus.
How do you calculate the mass of the neutrons in the helium-4 nucleus?
-The mass of a neutron is 1.00866490 amus. For two neutrons, the total mass is 2.0173298 amus.
What is the predicted mass of the helium-4 nucleus, and how is it calculated?
-The predicted mass of the helium-4 nucleus is the sum of the mass of the protons and neutrons. This equals 4.03188274 amus, calculated by adding 2.01455294 amus (for protons) and 2.0173298 amus (for neutrons).
What is the actual mass of the helium-4 nucleus, and how does it compare to the predicted mass?
-The actual mass of the helium-4 nucleus is 4.00150608 amus, which is slightly less than the predicted mass of 4.03188274 amus, resulting in a mass defect.
What is the mass defect, and how is it calculated?
-The mass defect is the difference between the predicted mass and the actual mass of the nucleus. It is calculated by subtracting the actual mass (4.00150608 amus) from the predicted mass (4.03188274 amus), which results in a mass defect of 0.03037666 amus.
How does the mass defect relate to the release of energy during the formation of the helium-4 nucleus?
-The mass defect represents the mass that was converted into energy when the nucleus was formed. According to Einstein's equation, E = mc², this energy can be calculated by converting the mass defect into kilograms and applying the speed of light.
How do you convert the mass defect from amus to kilograms, and what is the resulting value?
-To convert the mass defect from amus to kilograms, multiply by the conversion factor 1.66054 × 10⁻²⁷ kg/amu. This results in a mass of 5.04417 × 10⁻²⁹ kilograms.
How is the energy released during the formation of the helium-4 nucleus calculated?
-The energy released is calculated using Einstein's equation, E = mc². Using the mass of 5.04417 × 10⁻²⁹ kg and the speed of light (2.99792 × 10⁸ m/s), the energy is found to be approximately 4.53346 × 10⁻¹² Joules.
What is the nuclear binding energy, and how is it related to the energy released when the helium-4 nucleus forms?
-The nuclear binding energy is the energy released when the nucleus is formed, which is the same amount of energy required to break the nucleus apart. It is calculated as the energy released during the formation of the nucleus, 4.53346 × 10⁻¹² Joules in this case.
Why is the helium-4 nucleus stable despite the repulsion between its positively charged protons?
-The stability of the helium-4 nucleus is due to the nuclear strong force, which overcomes the repulsion between the positively charged protons and holds the nucleus together.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

A 'cheatsheet' on Binding Energy in nuclear physics
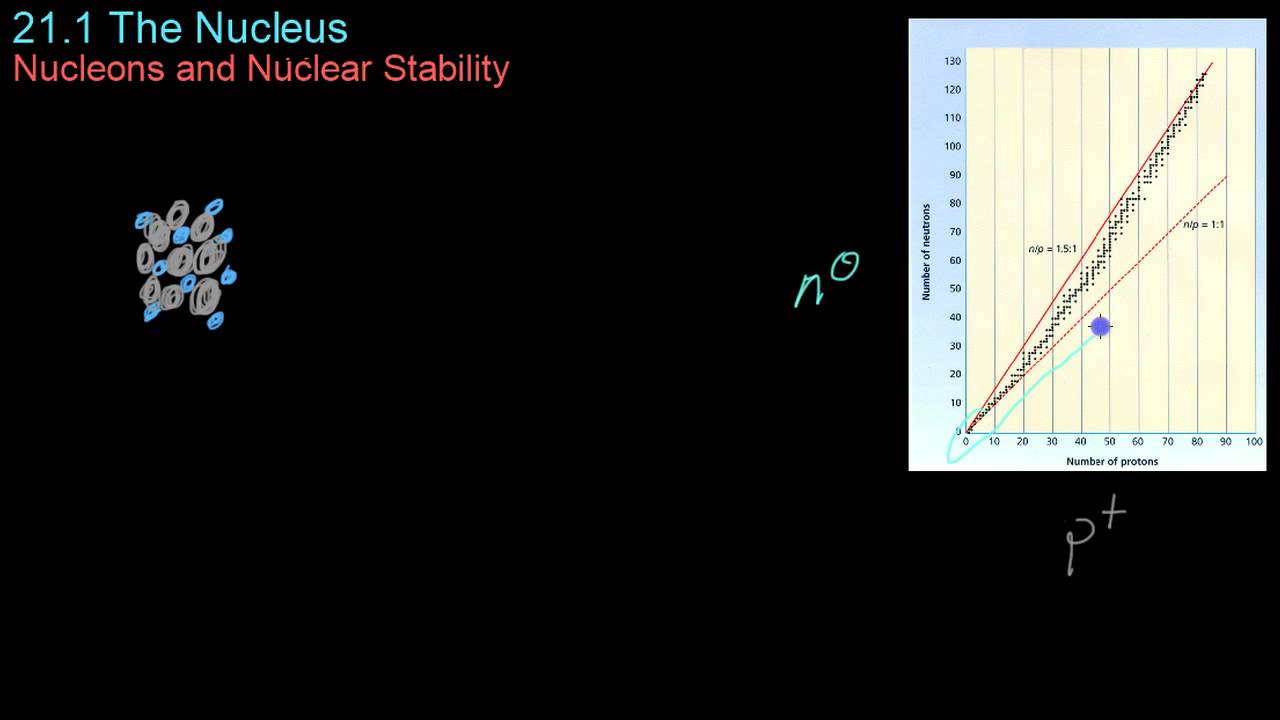
21.1 The Nucleus

Fisika Inti • Part 1: Defek Massa dan Energi Ikat Inti

Nuclear Chemistry Part 2 - Fusion and Fission: Crash Course Chemistry #39

Nuclear Fusion Explained
Nuclear Fusion | Fusion energy explained with Hydrogen atom example | Physics animation video
5.0 / 5 (0 votes)
