Matematika kelas X - Sistem Persamaan Linear part 1 - Sistem Persamaan Linear Dua Variabel (SPLDV)
Summary
TLDRIn this video, the host explains methods for solving systems of linear equations with two variables (SPLDV) using graphical, substitution, and elimination techniques. The video demonstrates how to graph lines and find intersection points, which represent the solution to the system. It also covers substitution and elimination methods for determining the values of variables with accuracy. The host offers step-by-step examples, emphasizes the importance of precise graphing, and discusses potential challenges with scaling. Additionally, a more efficient 'combined method' is introduced for solving problems. The tutorial aims to help students grasp linear equations concepts in a clear and practical way.
Takeaways
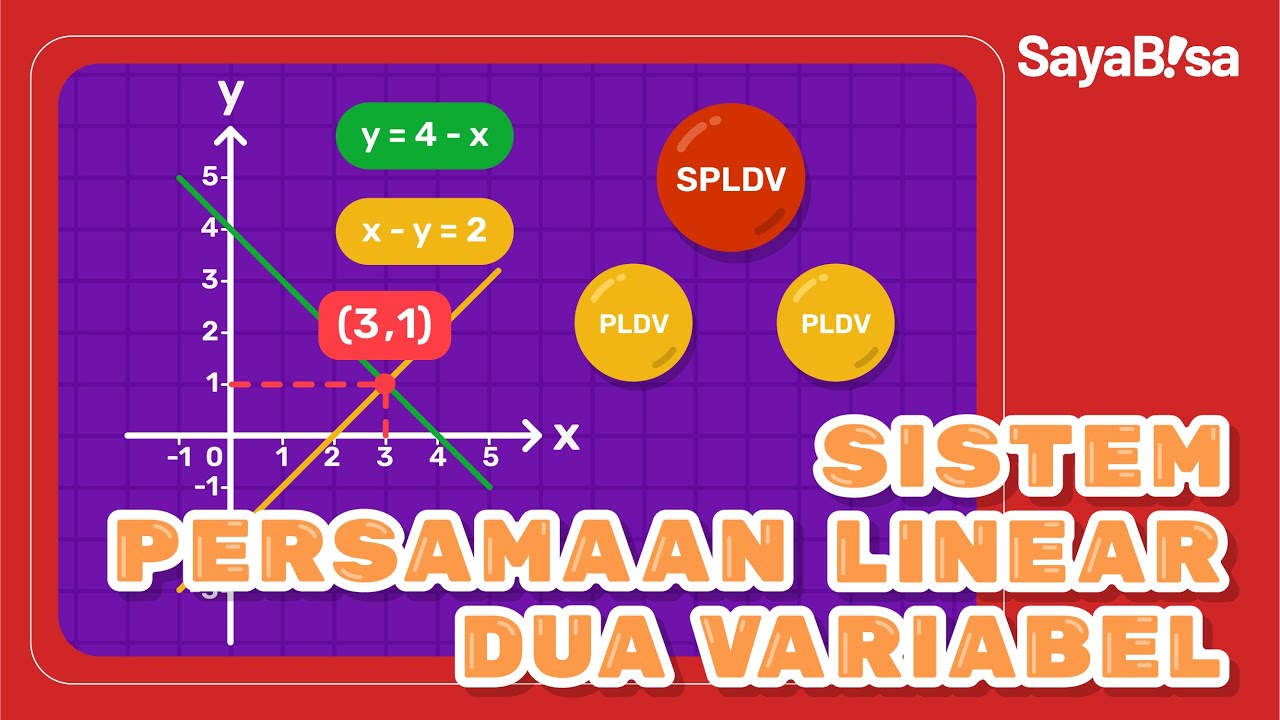
- 😀 The graphical method involves plotting equations on a coordinate plane, and the solution is the point of intersection between the lines.
- 😀 In the graphical method, accurate scaling of the graph is crucial for getting a correct solution.
- 😀 The substitution method involves solving one equation for a variable and substituting it into the other equation to find the solution.
- 😀 The elimination method eliminates one variable by adding or subtracting equations to cancel out a variable and solve for the remaining one.
- 😀 A key aspect of the elimination method is ensuring that the coefficients of one variable are the same in both equations before adding or subtracting.
- 😀 The combined method is a hybrid approach that uses both elimination and substitution for greater efficiency and accuracy in solving equations.
- 😀 It's important to consider the structure of the equations and the ease of isolating variables when choosing between substitution, elimination, or graphical methods.
- 😀 When solving systems with two variables, using graphical methods can be helpful for visualizing the solution, but it requires careful attention to scale.
- 😀 The substitution method is often the quickest when one equation is easy to solve for one variable, as it avoids the need for manipulation of both equations.
- 😀 The elimination method works best when the coefficients of one variable in both equations are easily adjusted for cancellation, simplifying the process.
- 😀 In the next tutorial, the focus will shift to solving systems of equations with three variables, which requires understanding three-dimensional graphing.
Q & A
What is the main focus of the video?
-The video focuses on teaching students how to solve systems of linear equations with two and three variables, using methods such as graphical, substitution, elimination, and combined approaches.
What does the graphical method for solving linear equations involve?
-The graphical method involves plotting the equations on a graph and finding the intersection point of the lines. This intersection represents the solution to the system of equations.
Why is it important to use a correct scale in the graphical method?
-A correct scale ensures that the graph is accurate, which in turn ensures that the intersection point is found correctly. If the scale is wrong, the intersection point may not be accurate.
What is the purpose of the substitution method in solving systems of equations?
-The substitution method involves solving one of the equations for a variable and substituting that expression into the other equation, simplifying it to find the solution for the remaining variable.
How does the elimination method work?
-The elimination method involves manipulating the equations to eliminate one of the variables by adding or subtracting the equations. This allows solving for the remaining variable.
What is the advantage of using the combined approach (elimination and substitution)?
-The combined approach allows for more flexibility and efficiency. After eliminating one variable, substitution can be used to solve for the other variable, streamlining the solution process.
In the elimination method, how do you know which variable to eliminate?
-You typically eliminate the variable whose coefficient is easiest to manipulate. This might involve multiplying one or both equations by a constant to align the coefficients of one variable so that they can be eliminated.
What happens if the graphical method does not give an accurate result?
-If the graphical method is inaccurate due to scale issues, it is recommended to use either the substitution or elimination method, which are more precise and do not depend on graphical accuracy.
What does the term 'HP' refer to in the context of solving systems of equations?
-In this context, 'HP' refers to the 'himpunan penyelesaian' or solution set, which is the point or points where the two equations intersect, representing the values of the variables that satisfy both equations.
How is the substitution method applied when working with equations that contain fractions or decimals?
-To avoid complications with fractions or decimals, the equations can be multiplied by a suitable factor (such as the least common denominator) to eliminate fractions and simplify the substitution process.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示
Sistem Persamaan Linear Dua Variabel | Matematika | SayaBisa

Kurikulum Merdeka Matematika Kelas 9 Bab 1 Sistem Persamaan Linear Dua Variabel

Sistem persamaan linear dua variabel kelas 10 - metode grafik

SPLDV - Metode Eliminasi

Sistem Persamaan Linear Dua Variabel Part 3 ~ Penerapan Konsep SPLDV dalam Menyelesaikan Masalah

Pair of Linear Equations in two variables| Part-1| Class 10| Introduction |Mathematics NCERT / CBSE
5.0 / 5 (0 votes)
