03. Derivative using definition as limit
MateFacil
21 Apr 201803:58
Summary
The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.
Please replace the link and try again.
Takeaways
- 😀 関数f(x) = 5xの導関数を定義に基づいて計算する方法を紹介しています。
- 😀 導関数の定義は、リミットの式に基づいて計算します。
- 😀 最初にf(x + h)を求める方法は、xをx + hに置き換えることです。
- 😀 f(x + h) = 5(x + h) = 5x + 5hの計算結果を得ることができます。
- 😀 次に、導関数の定義式にf(x + h)とf(x)を代入します。
- 😀 式はf'(x) = lim(h→0) [(5x + 5h) - 5x] / h となります。
- 😀 5x - 5xを引いて0を得るので、式は5h / hに簡略化されます。
- 😀 h/hが1になるので、結果は5となります。
- 😀 hが0に近づくとき、残った式にはhが含まれないため、結果は5です。
- 😀 この結果は、f(x) = 5xの導関数が常に5であることを示しています。
- 😀 次回のビデオでは、一般的な線形関数の導関数を計算する方法を解説します。
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

01. Derivative using definition as limit

Konsep Dasar Turunan Fungsi Aljabar Matematika Wajib Kelas 11 m4thlab
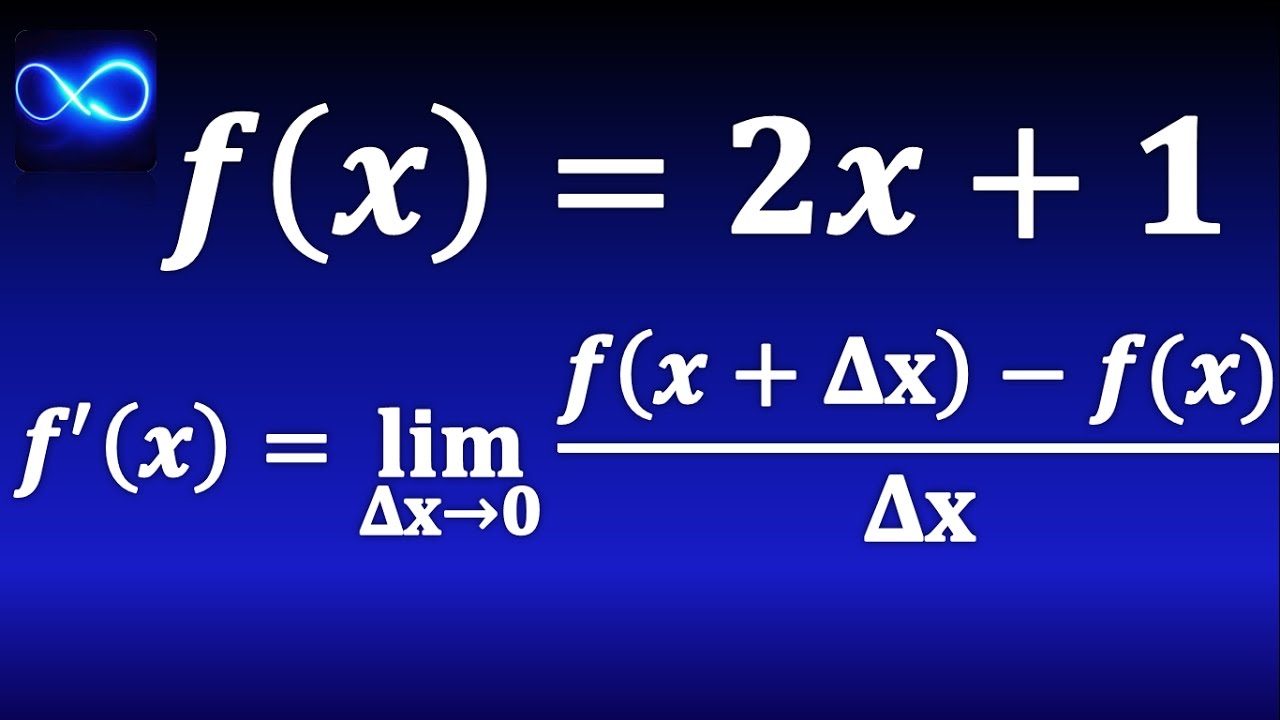
Derivative by increment method (By definition with limit)

Definition of the Derivative

Derivative definition
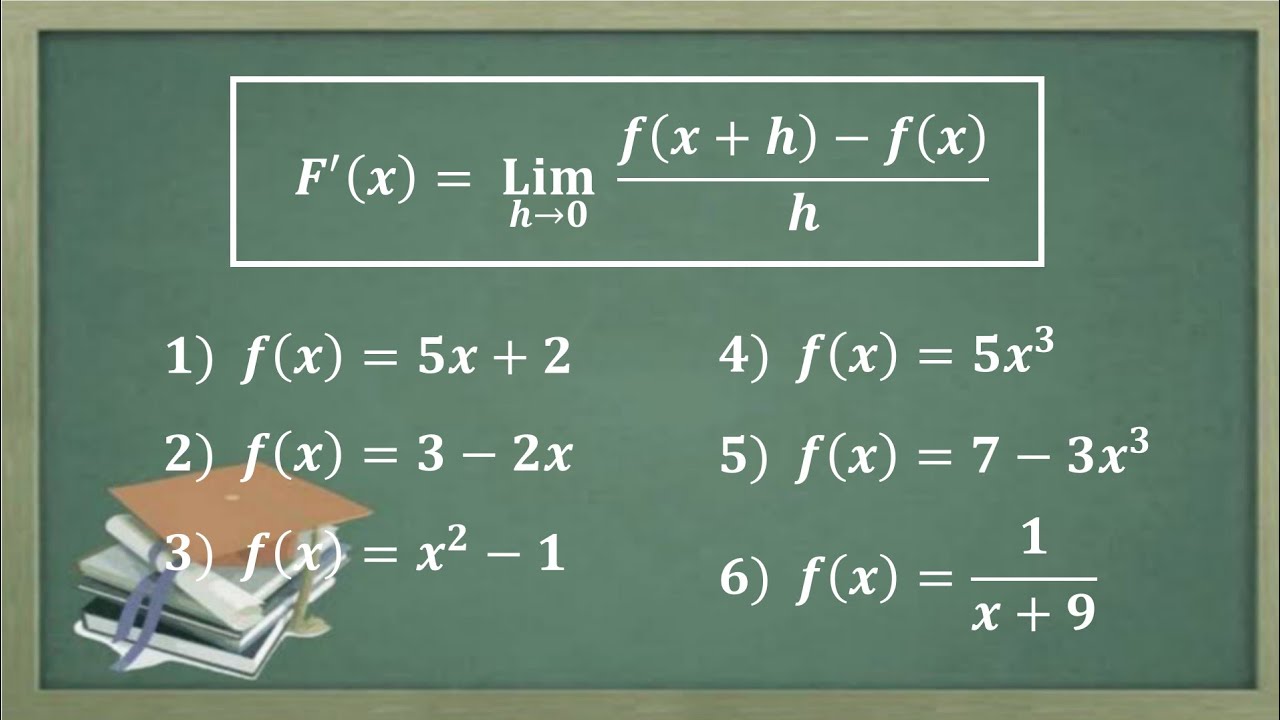
Turunan dengan menggunakan defnisi turunan Turunan menggunakan limit
Derivatives... What? (NancyPi)
Rate This
★
★
★
★
★
5.0 / 5 (0 votes)